当前位置：首页 > news >正文

【论文阅读】Multi-metrics adaptively identifies backdoors in Federated Learning

news 2025/8/21 8:54:25

这篇论文聚焦联邦学习（FL）的后门攻击防御，核心是通过「多指标融合 + 动态加权（白化处理）」解决现有防御 “对隐蔽攻击无效、高维下失效、依赖数据分布假设” 的痛点。

一、先读 “门面”：标题与摘要（3 分钟抓核心）

1. 标题拆解

核心动作：Multi-metrics adaptively identifies（多指标自适应识别）
应用场景：backdoors in Federated Learning（联邦学习中的后门攻击）
核心创新：用 “多指标” 替代 “单指标”，用 “动态加权” 适配不同数据分布与攻击类型。

2. 摘要精读（提炼「问题→方法→贡献→结果」）

（1）问题（现有防御的 3 大痛点）

高维失效：欧氏距离（ $L_2$ ）在高维空间（如神经网络参数）中 “失去意义”（所有点距离差异趋近于 0，无法区分恶意 / 良性梯度）；
单指标局限：单一指标（如欧氏距离、余弦相似度）只能识别特定类型恶意梯度，无法覆盖 “梯度尺度小”“角度偏移大” 等多样攻击；
假设依赖：多数防御依赖 “攻击类型已知”“数据 IID 分布” 等假设，对隐蔽攻击（如 Edge-case PGD）或非 IID 数据无效。

（2）方法（作者的解决方案）

引入曼哈顿距离（L1）：理论证明其在高维空间比欧氏距离更能保留 “距离差异”，缓解维度灾难；
多指标融合：用「曼哈顿距离（高维区分）+ 欧氏距离（梯度长度）+ 余弦相似度（梯度角度）」组成梯度特征，覆盖不同恶意梯度特性；
动态加权（白化处理）：通过协方差矩阵逆变换，消除指标尺度差异，自适应适配非 IID 数据与不同攻击，生成统一评分；
良性梯度聚合：按评分筛选发散度低的梯度（恶意梯度通常发散），用 FedAvg 聚合。

（3）贡献（3 个核心价值）

理论创新：首次证明曼哈顿距离在高维 FL 参数空间的有效性，提出无假设依赖的自适应防御框架；
方法创新：多指标 + 动态加权，突破 “单指标只能防特定攻击” 的局限；
实践价值：不牺牲主任务精度，在最难的 Edge-case PGD 攻击下仍有效。

（4）结果（关键实验指标）

最难攻击（Edge-case PGD）下，后门准确率（BA）低至 3.06%（Flame 为 5.12% 但主任务准确率 MA 降 6%，作者方法 MA 几乎不变）；
6 个数据集（图像、文本、金融）、4 种攻击类型下，均优于 Krum、Foolsgold、Weak-DP 等 SOTA 方法；
适应不同非 IID 程度（α=0.2~0.9）与攻击者比例（接近 50%），鲁棒性稳定。

二、再读 “背景”：引言与相关工作（理解 “为什么做”）

引言的核心是「讲清研究缺口（Gap）」—— 现有方法不够好，所以需要新方案。

1. 联邦学习（FL）的背景与风险

（1）FL 的核心优势

分布式训练：客户端不共享数据，仅上传模型更新（梯度 / 参数），解决数据隐私问题（如符合 GDPR）；
应用场景：图像处理（CIFAR-10）、医疗影像、边缘计算等，但去中心化特性导致易受后门攻击。

（2）FL 后门攻击的特殊性

目标：让模型对「攻击者指定输入（如带微小水印的图像）」输出错误标签，不影响正常输入的预测（隐蔽性强）；
难点：恶意梯度与良性梯度差异小（如通过缩放、梯度投影伪装），比 “无目标投毒攻击” 更难检测。

2. 现有防御的 2 类方法及缺陷

作者将现有防御分为两类，直指其核心不足：

防御类型	代表方法	核心逻辑	致命缺陷
评分基（区分梯度）	Krum、Foolsgold、RFA	用单指标（欧氏距离、余弦相似度）给梯度评分，筛选 “正常” 梯度	1. 依赖假设（如 Foolsgold 假设攻击者梯度一致，Krum 假设数据 IID）；2. 单指标易被绕过（如 PGD 攻击缩放梯度 norm 欺骗 Krum）
差分隐私（DP）	Weak-DP、Flame	给全局模型加高斯噪声，稀释恶意梯度影响	1. 显著降低主任务准确率（MA）与收敛速度；2. 噪声过大导致模型性能不可用

3. 作者的研究动机（解决 2 个关键问题）

高维距离失效问题：FL 模型参数是高维向量（如 VGG-9 有百万级参数），欧氏距离因 “维度灾难” 无法区分恶意 / 良性梯度；
单指标覆盖不足问题：不同攻击生成的恶意梯度特性不同（如 Model Replacement 梯度尺度大，PGD 梯度角度偏移），单指标无法全覆盖。

三、必懂 “基础”：核心概念与威胁模型（避免理解障碍）

论文涉及联邦学习、后门攻击、高维统计的核心概念，需先理清：

1. 关键术语解释

非 IID 数据：客户端数据分布不一致（如 A 客户端只有猫图像，B 只有狗图像），FL 中常见场景，会导致良性梯度差异大，防御易误判；
Edge-case PGD 攻击：最难的隐蔽攻击 —— 用 “边缘样本”（正常数据中极少出现，如罕见角度的汽车）投毒，同时将恶意梯度投影到 $L_2$ 球内，让防御难以识别；
维度灾难：高维空间中，所有点的欧氏距离趋近于相同，“近邻” 概念失效（比如 1000 维空间中，两个随机向量的距离差异几乎为 0）；
白化处理（Whitening）：对数据做线性变换，使其协方差矩阵为单位矩阵，消除不同指标的尺度差异，同时适配数据分布变化（如非 IID 下的梯度分布）。

2. 威胁模型（明确攻击者能力与目标）

攻击者目标：

对后门数据 $D_A$ ，模型输出错误标签 $l^{'}$ ；对正常数据，输出正确标签（不影响主任务，隐蔽性）；

公式表示： $G′(x)={l′≠G(x)x∈DAG(x)x∉DAG'(x)=\begin{cases}l'\neq G(x) & x\in D_A \\ G(x) & x\notin D_A\end{cases}$ （ $G^{'}$ 为被污染模型， $G$ 为正常模型）。
攻击者能力：

白盒（知道聚合算法与防御策略）、每次参与训练、控制少于 50% 客户端，但无法篡改服务器聚合逻辑。

四、精读 “方法”：多指标自适应防御框架（核心技术）

作者的防御框架分 3 步：「定义梯度特征→动态加权评分→筛选聚合良性梯度」，结构如下图
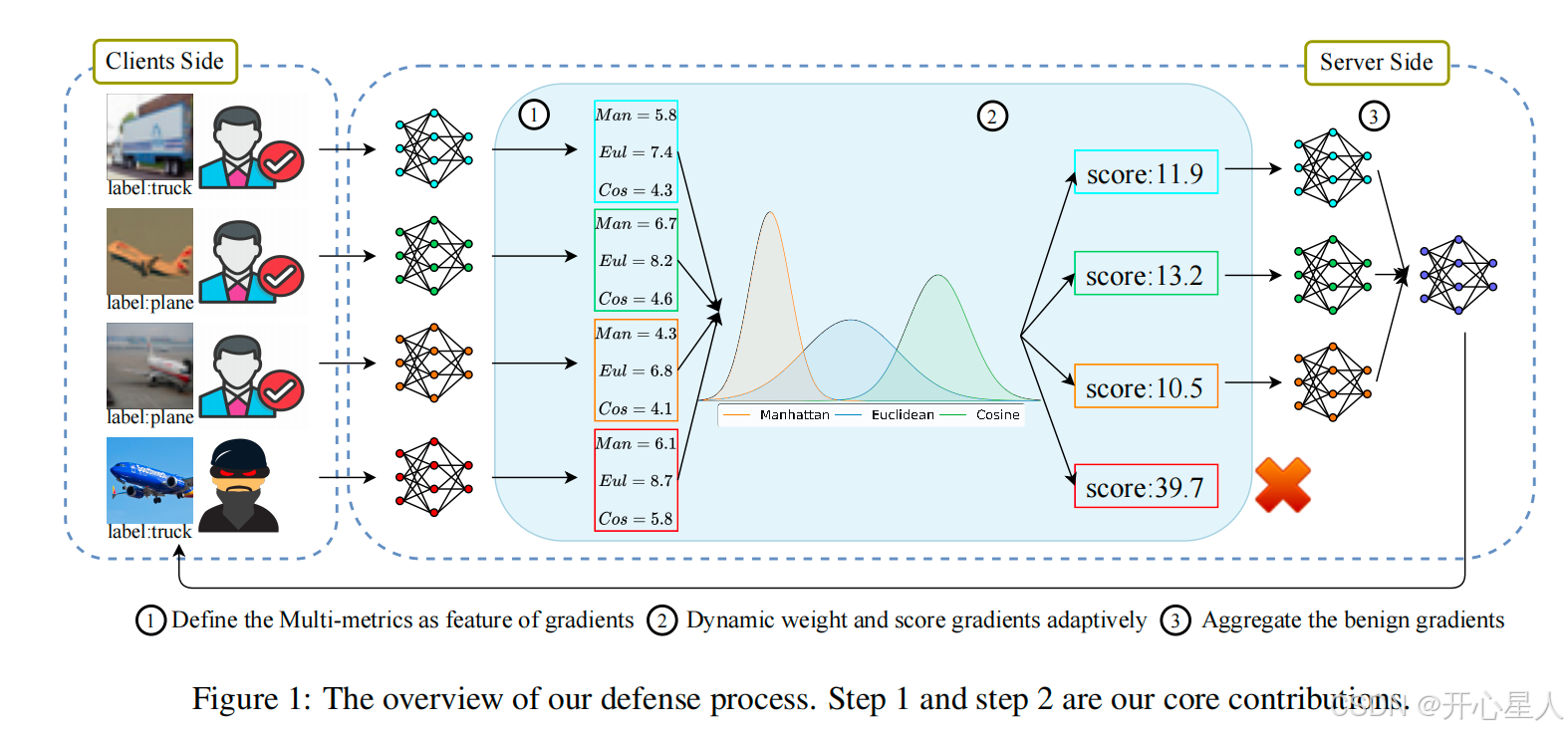
在这里插入图片描述

1. 第一步：定义梯度特征（解决 “单指标 + 高维失效”）

核心是用 “3 个互补指标” 描述梯度，同时用曼哈顿距离缓解高维问题。

（1）3 个指标的选择逻辑

指标类型	计算方式	作用（识别哪种恶意梯度）
曼哈顿距离（ $L_1$ ）	$x_{Man}^{(i)}=\|w_i - w_0\|_1$	高维空间区分梯度差异（缓解维度灾难，识别 PGD 类攻击）
欧氏距离（ $L_2$ ）	$x_{Eul}^{(i)}=\|w_i - w_0\|_2$	衡量梯度尺度（识别 Model Replacement 类 “大尺度恶意梯度”）
余弦相似度	$xCos(i)=<w0,wi>∣w0∣⋅∣wi∣x_{Cos}^{(i)}=\frac{<w_0,w_i>}{\|w_0\|\cdot\|w_i\|}$	衡量梯度角度（识别角度偏移大的恶意梯度）

符号说明： $w_0$ 是全局模型参数， $w_i$ 是第 $i$ 个客户端的局部模型参数， $_1$ / $_2$ 是 $L_1$ / $L_2$ 范数， $< \cdot,\cdot >$ 是内积。

（2）理论证明：曼哈顿距离在高维更有效

作者通过 3 个理论结论支撑 “选 $L_1$ 而非 $L_2$ ”：

定理 1（维度灾难）：当维度 $d \to \infty$ 时， $L_k$ 距离的 “最远 - 最近距离比” 趋近于 0（即所有点距离无差异）， $L_2$ 受影响更严重；
引理 1： $L_k$ 距离的 “最远 - 最近差异” 随维度 $d$ 增长的速率为 $d^{(1/k)-(1/2)}$ —— $k = 1$ （ $L_1$ ）时速率为 $d^{1/2}$ ， $k = 2$ （ $L_2$ ）时速率为 $d^0=1$ ，即 $L_1$ 的差异增长更快；
命题 1： $L_1$ 的区分能力（ $M_d$ ）是 $L_2$ （ $U_d$ ）的 $d^{1/2}$ 倍，高维下 $L_1$ 能保留更明显的距离差异，可区分恶意 / 良性梯度。

（3）梯度异常指标计算

为了捕捉 “某梯度是否与其他梯度发散”（恶意梯度通常更发散），计算每个梯度与其他所有梯度的 “指标差异和”：

$∑j≠i∣xCos(i)−xCos(j)∣)x'^{(i)}=\left( \sum_{j≠i} |x_{Man}^{(i)}-x_{Man}^{(j)}|,\ \sum_{j≠i} |x_{Eul}^{(i)}-x_{Eul}^{(j)}|,\ \sum_{j≠i} |x_{Cos}^{(i)}-x_{Cos}^{(j)}| \right)$

$x'^{(i)}$ 越大，说明第 $i$ 个梯度的指标与其他梯度差异越大，越可能是恶意梯度。

2. 第二步：动态加权评分（解决 “尺度差异 + 非 IID 适配”）

直接将 $x'^{(i)}$ 的 3 个分量相加会受 “尺度差异” 影响（如曼哈顿距离数值可能是余弦相似度的 100 倍），且非 IID 数据会导致梯度分布变化，因此作者用白化处理动态调整权重：

（1）白化处理的公式

对每个梯度的 $x'^{(i)}$ ，计算其 “发散度评分” $δ(i)\delta^{(i)}$ ：

$δ(i)=x′(i)⊤⋅Σ−1⋅x′(i)\delta^{(i)}=\sqrt{x'^{(i)\top} \cdot \Sigma^{-1} \cdot x'^{(i)}}$

$Σ\Sigma$ ：所有客户端 $x'^{(i)}$ 组成的协方差矩阵（反映 3 个指标的相关性与尺度）；
$Σ−1\Sigma^{-1}$ ：协方差矩阵的逆，作用是 “消除指标间的相关性，让各指标方差一致”，实现动态加权（如某轮攻击中角度差异更重要， $Σ−1\Sigma^{-1}$ 会自动提升余弦相似度的权重）。

（2）为什么不用 “Max 归一化”？

消融实验（表 4）证明：Max 归一化（将指标缩放到 [0,1]）在 Edge-case PGD 下后门准确率 BA=62.24%，而白化处理后 BA=3.06%—— 因为 Max 归一化无法适配非 IID 数据的梯度分布变化，易将 “非 IID 导致的良性梯度差异” 误判为恶意。

3. 第三步：良性梯度聚合（保留有效梯度）

筛选逻辑： $δ(i)\delta^{(i)}$ 越大，梯度越发散（越可能是恶意），因此移除 $K \cdot (1 - p)$ 个 $δ(i)\delta^{(i)}$ 最大的梯度（ $K$ 是本轮参与客户端数， $p$ 是筛选比例，如 $p = 0.5$ 保留前 50%）；
聚合方式：对筛选后的良性梯度，用标准 FedAvg 聚合（按客户端数据量加权）：

$w∗=w0+η⋅∑i∈Bn(i)⋅(wi−w0)∑i∈Bn(i)w^* = w_0 + \eta \cdot \frac{\sum_{i\in B} n^{(i)} \cdot (w_i - w_0)}{\sum_{i\in B} n^{(i)}}$

$B$ 是筛选后的良性客户端集合， $n^{(i)}$ 是第 $i$ 个客户端的数据量， $η\eta$ 是学习率。

五、读懂 “实验”：验证防御的有效性（用数据说话）

实验围绕「3 个核心问题」展开，覆盖 “不同攻击、不同数据分布、不同攻击强度”，证明方法的通用性与鲁棒性。
在这里插入图片描述

1. 实验设置（确保结果可信）

（1）数据集（覆盖多任务，非 IID 设置）

数据集	任务类型	规模	非 IID 设置（Dirichlet 分布 α）
CIFAR-10	图像分类	5 万训练 / 1 万测试	α=0.5（中等非 IID）
EMNIST	手写数字分类	28 万训练 / 7 万测试	α=0.5
CINIC10	图像分类	27 万图像	α=0.5
LOAN（金融）	贷款状态预测	226 万样本	按美国州划分客户端（α=0.9）
Sentiment140	推特情感分类	160 万推文	α=0.5

α 越小，非 IID 程度越高（如 α=0.2 时客户端数据分布差异极大）。

（2）模型与攻击类型

模型：按任务适配（VGG-9 for CIFAR-10、LeNet-5 for EMNIST、LSTM for Sentiment140）；
攻击类型（从易到难）：

Model Replacement：恶意客户端缩放梯度，试图替换全局模型；
DBA：将后门触发图案拆分到多个恶意客户端，梯度差异小；
PGD：将恶意梯度投影到 $L_2$ 球内，绕过欧氏距离基防御；
Edge-case PGD：用边缘样本投毒 + PGD 梯度投影，最难防御。

（3）评估指标

BA（后门准确率）：模型对后门数据的预测准确率，越低越好（攻击者目标是最大化 BA）；
MA（主任务准确率）：模型对正常数据的预测准确率，越高越好（防御不能牺牲正常功能）。

2. 核心实验结果（3 个关键结论）

（1）对比 SOTA：在最难攻击下表现最优

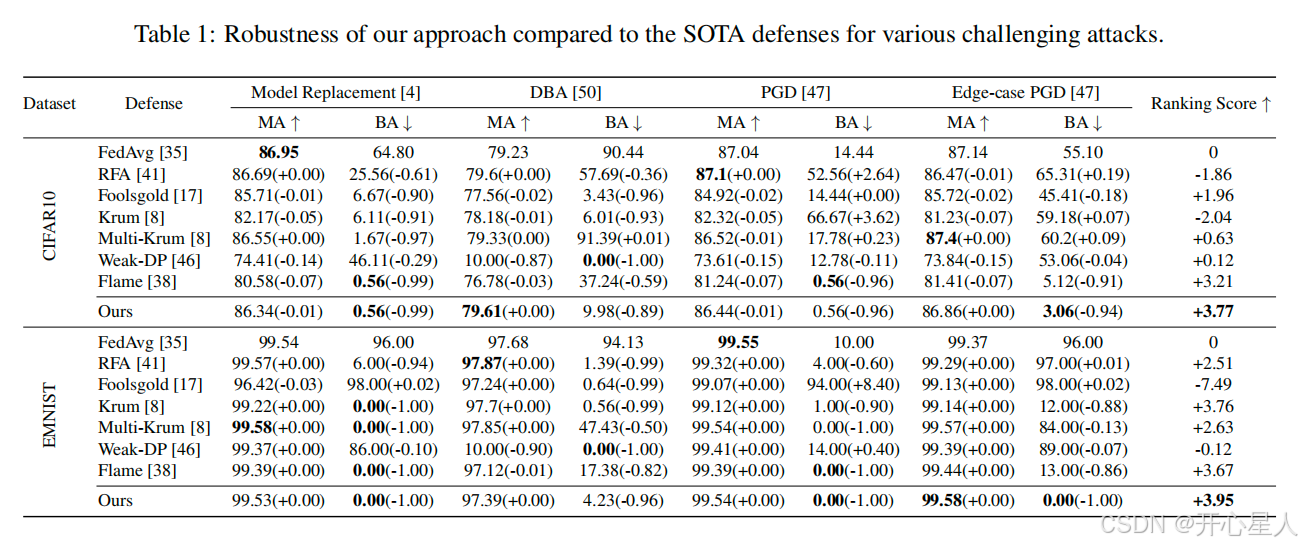
表 1（CIFAR-10 Edge-case PGD 攻击）结果：

防御方法	BA（后门准确率）	MA（主任务准确率）
FedAvg（ baseline）	55.10%	87.14%
Flame（DP-based）	5.12%	81.41%（降 5.73%）
作者方法	3.06%（最低）	86.86%（几乎不变）

结论：作者方法在 BA 最低的同时，MA 几乎无损失，优于 DP-based 方法（Flame）和评分基方法（Krum、Foolsgold）。

（2）适配非 IID 与攻击强度：鲁棒性稳定

非 IID 程度影响（图 4）：α 从 0.2（高非 IID）到 0.9（低非 IID），作者方法 BA 始终 < 5%，MA 稳定在 85%+；
攻击者比例影响（图 5）：攻击者占比从 10% 升至 45%，作者方法 BA 仍低于其他方法（如 EMNIST 下，攻击者 45% 时 BA=10%，而 Krum=40%）；
攻击频率影响（图 6）：攻击间隔从 1（每次攻击）到 10（每 10 轮攻击），BA 始终 < 6%，无明显波动。

（3）消融实验：多指标 + 白化是关键

单指标 vs 多指标（表 3）：

单指标（如仅 Manhattan）在 Edge-case PGD 下 BA=64.80%，而多指标（Man+Eul+Cos）BA=3.06%—— 证明多指标能覆盖多样恶意梯度；
Max 归一化 vs 白化（表 4）：

Max 归一化在 Edge-case PGD 下 BA=62.24%，白化后 BA=3.06%—— 证明动态加权能适配非 IID 与攻击分布。

3. 泛化性验证：跨数据集有效

表 2 显示，在金融（LOAN）、文本（Sentiment140）数据集上：

LOAN：作者方法 BA=0%（后门完全失效），MA=88.52%（仅降 0.53%）；
Sentiment140：BA=5.83%，MA=81.67%（仅降 0.92%）；
结论：方法不依赖任务类型，泛化性强。

六、总结：核心贡献与未来方向

1. 核心贡献（3 点不可替代价值）

理论突破：首次证明曼哈顿距离在高维 FL 参数空间的有效性，为距离基防御提供理论支撑；
方法创新：多指标融合 + 白化动态加权，突破 “单指标 + 固定权重” 的局限，无需依赖攻击或数据分布假设；
实践价值：在最难的 Edge-case PGD 攻击下仍能保持低 BA（3.06%）与高 MA，且适配非 IID 数据与大规模数据集（如 OGBN-arXiv）。