代码随想录刷题——字符串篇(七)
459.重复的子字符串
移动匹配法:
bool repeatedSubstringPattern(string s) {# 组成新串string t=s+s;# 去除首尾字符t.erase(t.begin());t.erase(t.end()-1);# 判断中间是否有与原字符串相等的子串if(t.find(s)!=npos) return true;return false;}KMP法:
# 获取next数组 void getNext(int* next,const string& s){next[0]=0;int i=0;for(int j=1;j<s.size();j++){while(i>0&&s[i]!=s[j]){i=next[i-1];}if(s[i]==s[j]){i++;}next[j]=i;}} bool repeatedSubstringPattern(string s) {vector<int> next(s.size());getNext(&next[0], s);int n=s.size();# 如果next数组最后一位不为0则存在最长相等前后缀,再判断最长重复子串的长度# 是否可以被字符串长度整除即可if(next[n-1]!=0 && n%(n-next[n-1])==0) return true;return false;}
其他:
(1)移动匹配法非常巧妙,相当于把一个字符串写两遍,去掉首尾字符(因为一个字符串如果自循环构成长度一定大于等于2),再查找原字符串是否仍存在,如果存在则一定自循环,举个例子(空格是为了好观察):
s="abc abc abc"
t=s+s="abc abc abc abc abc abc"
去掉首位字符后=“bc abc abc abc abc ab"此时由于自循环的缘故,中间部分一定会出现与原始字符串相同的子串,充分必要性的数学证明网站中有
(2)字符串相关:
a.重载了+运算符
b. t.find(s)!=string::npos 判断写法,string作用域下的npos
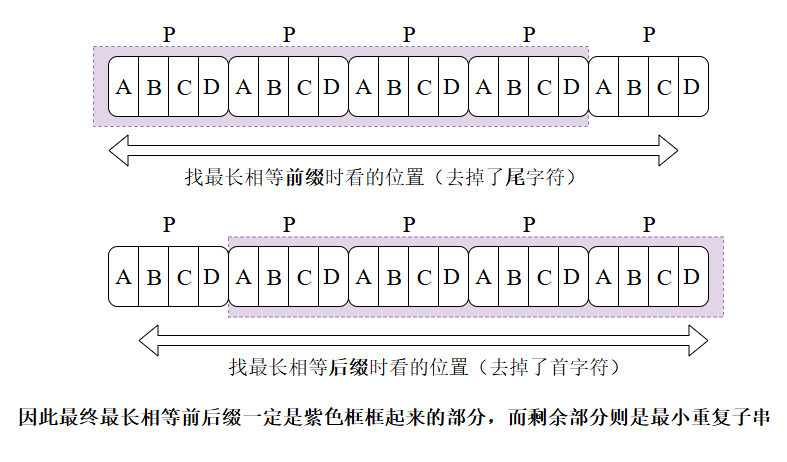
(3)KMP法则是利用最长相等前后缀来找最小重复子串,一个示意图就很清晰: