机械原理的齿轮怎么学?
学习机械原理中的 “齿轮” 部分,关键是从 “基础概念→核心原理→几何计算→实际应用” 逐步推进,既要抓理论逻辑,也要结合具象分析(比如齿廓形状、啮合过程)。以下是分步骤的学习思路,附重点和技巧:
第一步:先啃 “基础概念”—— 搞懂齿轮的 “身份卡”
齿轮的核心是 “通过齿廓啮合传递运动和动力”,所有复杂内容都基于基础参数,先把这些 “基本量” 记牢、分清:
- 齿轮的分类(先有 “宏观认知”)
按轴的位置关系分:直齿圆柱齿轮(平行轴)、斜齿圆柱齿轮(平行轴)、锥齿轮(相交轴)、蜗杆蜗轮(交错轴)。
机械原理中重点是 “直齿圆柱齿轮”(基础中的基础),学透后再扩展到斜齿、锥齿轮(它们是直齿的 “变形”,比如斜齿靠 “螺旋角” 实现平稳传动,锥齿轮靠 “节锥角” 适应相交轴)。
- 标准直齿圆柱齿轮的 “核心参数”(重中之重!)
这些参数是 “齿轮的身份证”,所有几何尺寸计算都围绕它们:
模数(m):单位 mm,是 “人为规定的标准值”(比如 1、2、2.5mm),用来统一齿的大小(m 越大,齿越粗壮)。公式:模数 m = 分度圆直径 d / 齿数 z(d=mz,这个公式刻进脑子里!)。
压力角(α):标准值 20°(我国),指 “分度圆上齿廓的压力角”(齿廓上某点的正压力方向与速度方向的夹角)。压力角影响传动效率和齿的强度。
齿数(z):齿轮上的齿的数量,直接影响齿轮大小(z 越多,齿轮直径越大,前提 m 相同)。
还有两个 “辅助参数”:齿顶高系数(hₐ*,标准值 1)、顶隙系数(c*,标准值 0.25),用来算齿顶高、齿根高(齿顶高 hₐ=hₐm,齿根高 hբ=(hₐ+c*)m)。
技巧:拿一个标准齿轮实物(或教材上的剖视图),对着参数标 “分度圆(d)、齿顶圆(dₐ=d+2hₐ)、齿根圆(dբ=d-2hբ)”,直观对应公式,比死记硬背有效。
第二步:突破 “核心原理”—— 理解 “齿廓为什么能平稳传动”
齿轮的关键是 “传动平稳”(转速均匀、无冲击),核心原理是 “齿廓啮合基本定律”,这部分别绕晕,抓本质:
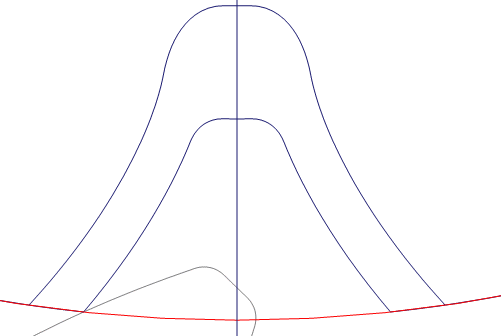
- 齿廓啮合基本定律(底层逻辑)
定律:“一对齿廓啮合时,其瞬时传动比等于两齿轮连心线被啮合点处公法线所截两线段的反比”。
白话解释:要让传动比 i₁₂=ω₁/ω₂=z₂/z₁(恒定,这样才平稳),必须让 “啮合点的公法线始终通过连心线上的一个定点(节点 P)”。这个定点 P 所在的圆就是 “分度圆”(所以分度圆是 “计算基准圆”,不是实际加工的圆)。
- 为什么用 “渐开线” 做齿廓?(重点 + 考点)
满足 “传动比恒定” 的齿廓有很多(比如摆线),但渐开线最常用,因为它有 3 个 “神仙性质”:
性质 1:“渐开线的形状只和基圆有关”(基圆 dᵦ=mzcosα,基圆越大,渐开线越 “平直”)。
性质 2:“渐开线上某点的法线必与基圆相切”(所以啮合时,两齿廓的公法线就是两基圆的内公切线,自然通过节点 P,保证传动比恒定)。
性质 3:“渐开线齿廓的啮合角恒定”(啮合角等于分度圆压力角 α,所以受力方向不变,传动平稳)。
技巧:搜 “渐开线形成动画”(比如基圆滚动时,线上某点的轨迹),直观看 “基圆→渐开线” 的关系;再看 “两渐开线齿廓啮合动画”,观察 “公法线始终过节点”,原理就通了。
第三步:掌握 “几何计算”—— 从 “单个齿轮” 到 “一对齿轮啮合”

这部分是 “硬功夫”,必须动手算,重点是 “标准直齿圆柱齿轮的尺寸计算” 和 “啮合传动条件”:
- 单个标准直齿圆柱齿轮的尺寸计算(公式汇总,直接套!)
已知 m、α(20°)、z,就能算所有圆的直径:
举例:m=2mm,z=20 的标准齿轮,d=2×20=40mm,dₐ=2×(20+2)=44mm,dᵦ=40×cos20°≈37.59mm—— 算一遍就记住公式了。
分度圆 d = mz
基圆 dᵦ = dcosα = mzcosα
齿顶圆 dₐ = d + 2hₐm = m(z+2hₐ)(hₐ*=1,所以 dₐ=m (z+2))
齿根圆 dբ = d - 2 (hₐ*+c*) m = m (z-2.5)(hₐ*+c*=1.25)
齿距 p(相邻两齿同侧齿廓在分度圆上的弧长):p=πm(所以 m=p/π,这是模数的物理意义)
齿厚 s(分度圆上一个齿的弧长):s=p/2=πm/2;齿槽宽 e=s=πm/2(标准齿轮 s=e)。
- 一对齿轮的 “正确啮合条件” 和 “连续传动条件”(必考!)
正确啮合条件:两齿轮的 “模数必须相等”(m₁=m₂),“压力角必须相等”(α₁=α₂)。
原因:模数不等,齿厚 / 齿槽宽不匹配,会 “卡住”;压力角不等,公法线不过节点,传动比不恒定。
连续传动条件:“重合度 ε>1”(实际 ε≥1.1~1.4)。
重合度:“同时啮合的齿的对数的平均值”(ε=1.3 表示平均有 1.3 对齿同时啮合)。如果 ε<1,前一对齿脱离啮合时,后一对齿还没接上,会有冲击。
计算:ε 和齿数 z、齿顶高系数有关(z 越多,ε 越大;所以小齿轮 z 不能太少,通常 z≥17,避免根切)。
第四步:拓展 “特殊问题”—— 根切、变位齿轮(解决实际问题)
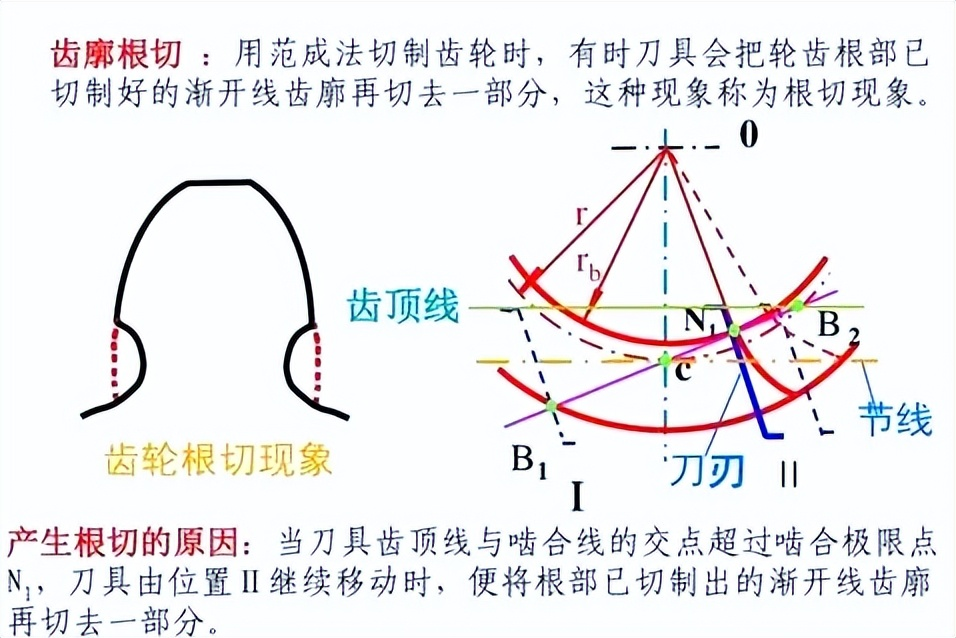
学完基础,要理解 “为什么实际齿轮不能随便做”:
根切现象:当齿轮齿数太少(z<17),加工时刀具会 “切到齿轮根部”(齿根被挖掉一块),导致齿根强度降低。
解决办法:“变位齿轮”(刀具远离 / 靠近齿轮中心,改变齿厚 / 齿槽宽),变位后 z 可以小于 17,还能凑中心距(比如实际中心距和理论值不等时,用变位齿轮调节)。
最后:学习技巧 ——“理论 + 具象 + 做题”
看动画 / 实物:搜 “齿轮啮合动画”“渐开线形成动画”,直观理解齿廓运动;找个旧齿轮,量齿顶圆、数齿数,反算模数(比如 dₐ=m (z+2)→m=dₐ/(z+2)),验证理论。
做习题:重点做 “尺寸计算”“啮合条件判断”“重合度计算” 题(教材课后题足够),比如 “已知一对齿轮 m=2,z₁=20,z₂=50,求中心距 a(a=(d₁+d₂)/2=m (z₁+z₂)/2=70mm)”,通过做题巩固公式。
联系应用:比如自行车的齿轮(大齿轮带小齿轮,增速;小齿轮带大齿轮,减速),理解 “传动比 i=z₂/z₁” 的实际意义。
齿轮是机械原理中 “传动部分” 的核心,只要把 “参数→原理→计算” 的逻辑串起来,再结合具象分析,就不难学 —— 从直齿入手,学透后,斜齿、锥齿轮只是 “参数多了个螺旋角 / 节锥角”,原理相通!

