高等数学 8.6 空间曲线及其方程
文章目录
- 一、空间曲线的一般方程
- 二、空间曲线的参数方程
- *曲面的参数方程
- 三、空间曲线在坐标平面上的投影
一、空间曲线的一般方程
我们已经知道空间曲线可以看做两个曲面的交线。设
F(x,y,z)=0和G(x,y,z)=0F(x, y, z) = 0 \quad 和 \quad G(x, y, z) = 0 F(x,y,z)=0和G(x,y,z)=0
是两个曲面的方程,则方程组
{F(x,y,z)=0,G(x,y,z)=0.(6-1)\begin{equation*} \begin{cases} F(x, y, z) = 0, \\ G(x, y, z) = 0. \end{cases} \end{equation*} \tag{6-1} {F(x,y,z)=0,G(x,y,z)=0.(6-1)
就是这两个曲面的交线 CCC 的方程,方程组 (6−1)(6-1)(6−1) 也叫做 空间曲线 CCC 的一般方程 。

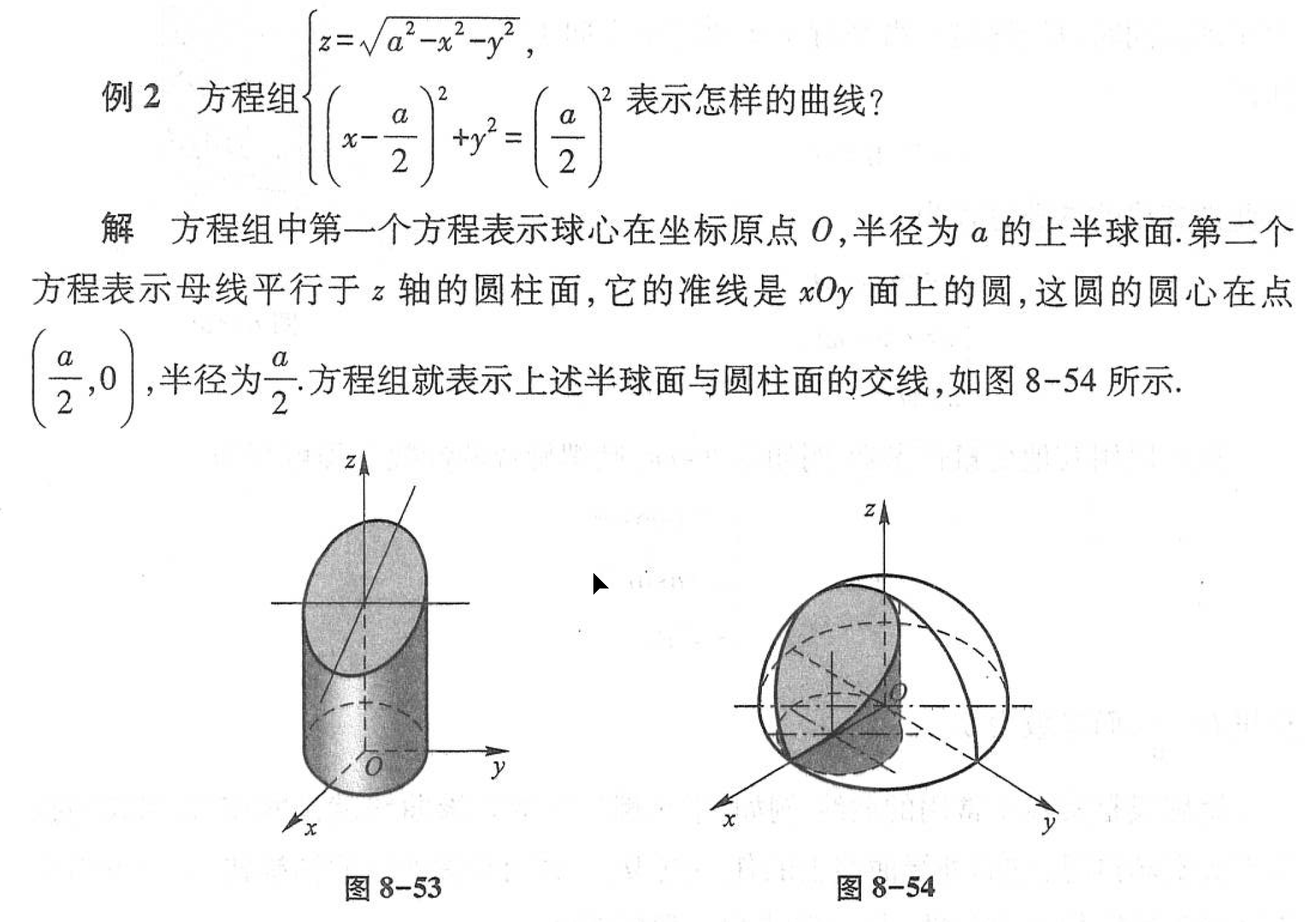
二、空间曲线的参数方程
空间曲线 CCC 的方程除了一般方程之外,也可以用参数形式表示,只要将 CCC 上动点的坐标 x,yx, yx,y 和 zzz 表示为参数 ttt 的函数
{x=x(t),y=y(t),z=z(t).(6-2)\begin{equation*} \begin{cases} x = x(t), \\ y = y(t), \\ z = z(t). \end{cases} \end{equation*} \tag{6-2} ⎩⎨⎧x=x(t),y=y(t),z=z(t).(6-2)
当给定 t=t1t = t_1t=t1 时,就得到曲线 CCC 上的一个点 (x1,y1,z1)(x_1, y_1, z_1)(x1,y1,z1) ;随着 ttt 的变动便可得曲线 CCC 上的全部点。方程组 (6−2)(6-2)(6−2) 叫做 空间曲线的参数方程 。

*曲面的参数方程
介绍一下曲面的参数方程。曲面的参数方程通常是含两个参数的方程,形如
{x=x(s,t),y=y(s,t),z=z(s,t).(6-3)\begin{equation*} \begin{cases} x = x(s, t), \\ y = y(s, t), \\ z = z(s, t). \end{cases} \end{equation*} \tag{6-3} ⎩⎨⎧x=x(s,t),y=y(s,t),z=z(s,t).(6-3)
例如空间曲线 Γ\GammaΓ
{x=φ(t),y=ψ(t),z=ω(t).(α⩽t⩽β)\begin{equation*} \begin{cases} x = \varphi(t), \\ y = \psi(t), \\ z = \omega(t). \end{cases} \quad (\alpha \leqslant t \leqslant \beta) \end{equation*} ⎩⎨⎧x=φ(t),y=ψ(t),z=ω(t).(α⩽t⩽β)
绕 zzz 轴旋转,所得旋转曲面的方程为
{x=[φ(t)]2+[ψ(t)]2cosθ,y=[φ(t)]2+[ψ(t)]2sinθ,z=ω(t).α⩽t⩽β,0⩽θ⩽2π(6-4)\begin{equation*} \begin{cases} x = \sqrt{[\varphi (t)]^2 + [\psi (t)]^2} \cos \theta, \\ y = \sqrt{[\varphi (t)]^2 + [\psi (t)]^2} \sin \theta, \\ z = \omega (t). \end{cases} \quad \alpha \leqslant t \leqslant \beta, 0 \leqslant \theta \leqslant 2 \pi \end{equation*} \tag{6-4} ⎩⎨⎧x=[φ(t)]2+[ψ(t)]2cosθ,y=[φ(t)]2+[ψ(t)]2sinθ,z=ω(t).α⩽t⩽β,0⩽θ⩽2π(6-4)
这是因为,固定一个 ttt ,得 Γ\GammaΓ 上一点 M1(φ(t),ψ(t),ω(t))M_1 (\varphi (t), \psi (t), \omega (t))M1(φ(t),ψ(t),ω(t)) ,点 M1M_1M1 绕 zzz 轴旋转,得空间的一个圆,该圆在平面 z=ω(t)z = \omega (t)z=ω(t) 上,其半径为点 M1M_1M1 到 zzz 轴的距离 [φ(t)]2+[ψ(t)]2\sqrt{[\varphi (t)]^2 + [\psi (t)]^2}[φ(t)]2+[ψ(t)]2 ,因此,固定 ttt 的方程 (6−4)(6-4)(6−4) 就是该圆的参数方程。再令 ttt 在 [α,β][\alpha, \beta][α,β] 内变动,方程 (6−4)(6-4)(6−4) 便是旋转曲面的方程。
例如直线
{x=1,y=t,z=2t.\begin{equation*} \begin{cases} x = 1, \\ y = t, \\ z = 2t. \end{cases} \end{equation*} ⎩⎨⎧x=1,y=t,z=2t.
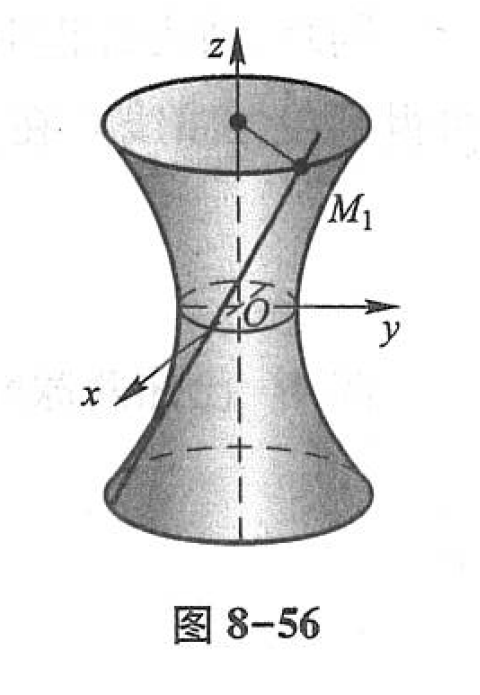
绕 zzz 轴旋转所得的旋转曲面(如图8-56)的方程为
{x=1+t2cosθ,y=1+t2sinθ,z=2t.\begin{equation*} \begin{cases} x = \sqrt{1+ t^2} \cos \theta, \\ y = \sqrt{1+ t^2} \sin \theta, \\ z = 2t. \end{cases} \end{equation*} ⎩⎨⎧x=1+t2cosθ,y=1+t2sinθ,z=2t.
(上式消去t和θ,得曲面的直角坐标方程为x2+y2=1+z24)\left( 上式消去t和\theta ,得曲面的直角坐标方程为 x^2 + y^2 = 1 + \cfrac{z^2}{4} \right)(上式消去t和θ,得曲面的直角坐标方程为x2+y2=1+4z2) 。
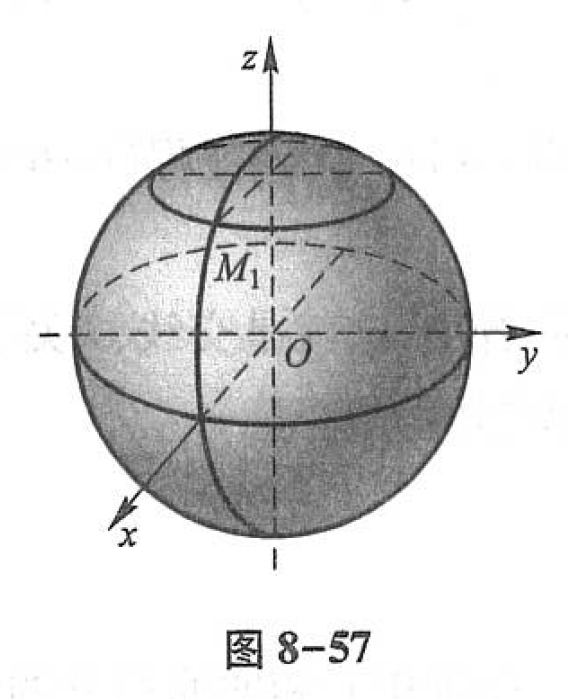
又如球面 x2+y2+z2=a2x^2 + y^2 + z^2 = a^2x2+y2+z2=a2 可以看成 zOxzOxzOx 面上的半圆周
{x=asinφ,y=0,z=acosφ,0⩽φ⩽π\begin{equation*} \begin{cases} x = a \sin \varphi, \\ y = 0, \\ z = a \cos \varphi, \end{cases} \quad 0 \leqslant \varphi \leqslant \pi \end{equation*} ⎩⎨⎧x=asinφ,y=0,z=acosφ,0⩽φ⩽π
绕 zzz 轴旋转所得(图8-57),故球面方程为
{x=asinφcosθ,y=asinφsinθ,z=acosφ,0⩽φ⩽π,0⩽θ⩽2π.\begin{equation*} \begin{cases} x = a \sin \varphi \cos \theta, \\ y = a \sin \varphi \sin \theta, \\ z = a \cos \varphi, \end{cases} \quad 0 \leqslant \varphi \leqslant \pi, 0 \leqslant \theta \leqslant 2 \pi. \end{equation*} ⎩⎨⎧x=asinφcosθ,y=asinφsinθ,z=acosφ,0⩽φ⩽π,0⩽θ⩽2π.
三、空间曲线在坐标平面上的投影
设空间曲线 CCC 的一般方程为 (6−1)(6-1)(6−1) ,现在来研究由方程组 (6−1)(6-1)(6−1) 消去变量 zzz 后(如果可能的话)所得的方程
H(x,y)=0(6-5)H(x, y) = 0 \tag{6-5} H(x,y)=0(6-5)
由于方程 (6−5)(6-5)(6−5) 是由方程组 (6−1)(6-1)(6−1) 消去 zzz 后所得的结果,因此当 x,yx, yx,y 和 zzz 满足方程组 (6−1)(6-1)(6−1) 时,前两个坐标 x,yx, yx,y 必定满足方程 (6−5)(6-5)(6−5) ,这说明曲线 CCC 上的所有点都在由方程 (6−5)(6-5)(6−5) 所表示的曲线上。
方程 (6−5)(6-5)(6−5) 表示一个母线平行于 zzz 轴的柱面。由上面的讨论可知,这柱面必定包含曲线 CCC 。以曲线 CCC 为准线、母线平行于 zzz 轴(即垂直于 xOyxOyxOy 面)的柱面叫做曲线 CCC 关于 xOyxOyxOy 面的 投影柱面 ,投影柱面与 xOyxOyxOy 面的交线叫做空间曲线 CCC 在 xOyxOyxOy 面上的 投影曲线 ,或简称 投影 。因此,方程 (6−5)(6-5)(6−5) 所表示的柱面必定包含投影柱面,而方程
{H(x,y)=0,z=0\begin{equation*} \begin{cases} H(x, y) = 0, \\ z = 0 \end{cases} \end{equation*} {H(x,y)=0,z=0
所表示的曲线必定包含空间曲线 CCC 在 xOyxOyxOy 面上的投影。
同理,消去方程组 (6−1)(6-1)(6−1) 中的变量 xxx 或变量 yyy ,再分别和 x=0x = 0x=0 或 y=0y = 0y=0 联立,我们就可得到包含曲线 CCC 在 yOzyOzyOz 面或 zOxzOxzOx 面上的投影的曲线方程
{R(y,z)=0,x=0,或{T(x,z)=0,y=0.\begin{equation*} \begin{cases} R(y, z) = 0, \\ x = 0, \end{cases} \quad 或 \quad \begin{cases} T(x, z) = 0, \\ y = 0. \end{cases} \end{equation*} {R(y,z)=0,x=0,或{T(x,z)=0,y=0.


原文链接:高等数学 8.6 空间曲线及其方程
