C++排序算法学习笔记

---

前言

在 C++ 中，快速排序、堆排序和插入排序是三种基础但特性迥异的排序算法。STL 的 std::sort 正是结合了三者的优点（Introsort）。以下是它们的详细实现和对比：

1. 排序算法的选定标准

1.1 时空复杂度

首先一个指标肯定是时间复杂度和空间复杂度。
对于任意一个算法，其时间复杂度和空间复杂度都是越小越好的。

1.2 稳定性

稳定性是排序算法的一个重要性质，我们可以简单总结为：
对于序列中的相同元素，如果排序之后它们的相对位置没有发生改变，则称该排序算法为「稳定排序」，反之则为「不稳定排序」。
如果单单排序 int 数组，那么稳定性没有什么意义。但如果排序一些结构比较复杂的数据，那么稳定排序就会有一定的优势。
如果你用稳定排序算法，那么排序完成后，相同用户 ID 的订单依然会按照交易日期有序排列：

   Date    UserID
2020-02-01  1001
2020-02-02  1001
2020-02-03  10012020-01-01  1002
2020-01-02  1002
2020-01-03  1002
...

因为之前已经按照日期排好序了，对用户 ID 稳定排序之后，相同用户 ID 的订单的相对位置保持不变，所以在日期上依然是有序的。

如果你用不稳定排序算法，相同用户 ID 的订单相对位置可能变化，所以对于相同用户 ID 的订单，交易日期的有序性会丧失，相当于你之前对日期的排序白做了。

可以看到，稳定性是个很重要的性质，所以你在使用排序算法时要特别注意，避免出现预期之外的结果。

1.3 原地排序

原地排序就是指排序过程中不需要额外的辅助空间，只需要常数级别的额外空间，直接操作原数组进行排序。

注意，关键是是否需要额外的空间，而不是是否返回一个新的数组。具体来说就是类似这样的区别：

// 非原地排序
void sort(int[] nums) {// 排序过程中需要额外的辅助数组，消耗 O(N) 的空间int[] tmp = new int[nums.length];// 对 nums 进行排序for ...
}// 原地排序
void sort(int[] nums) {// 直接操作 nums，不需要额外的辅助数组，消耗 O(1) 的空间for ...
}

不难想到，对于大数据量的排序，原地排序算法是比较有优势的。

2. 冒泡排序

冒泡排序（Bubble Sort）是一种简单且直观的排序算法。它通过重复地遍历要排序的列表，一次比较两个相邻的元素并交换它们的位置来排序列表。这个过程会一直重复，直到列表变得有序为止。由于每次遍历列表时最大的元素会“冒泡”到列表的末端，故称为冒泡排序。

关于冒泡排序的详细过程如下（按照升序描述）：

1. 从列表的第一个元素开始，依次比较相邻的两个元素。
2. 如果前一个元素比后一个元素大，则交换它们的位置。
3. 继续向后比较，直到列表的末尾。这时，最大的元素被放置到列表的末尾。
4. 重新从列表的第一个元素开始，重复上述过程，但不再处理已排序的最后一个元素。

持续重复步骤 1-4，直到没有需要交换的元素，表示列表已完成排序。

#include <iostream>
#include <vector>
using namespace std;// 升序
void bubbleSort(vector<int>& vec)
{int size = vec.size();bool swapped = false;for (int i = 0; i < size - 1; ++i){swapped = false;for (int j = 0; j < size - i - 1; ++j){if (vec[j] > vec[j + 1]){swap(vec[j], vec[j + 1]);   // 交换swapped = true;}}if (!swapped){break;  // 提前结束排序}}
}int main()
{srand(time(NULL));vector<int> data;cout << "排序前的原始数据: ";for (int i = 0; i < 10; ++i){data.push_back(rand() % 100);cout << data.back() << " ";}cout << endl;bubbleSort(data);cout << "排序之后的数据: ";for (const auto& item : data){cout << item << " ";}cout << endl;return 0;
}

冒泡排序的时间复杂度取决于输入数组的初始状态：

• 最坏情况下：每次遍历都需要进行比较和交换操作，因此时间复杂度为 O(n2)。
• 最优情况下：如果输入数组已经有序，只需进行一次遍历，时间复杂度为 O(n)。
• 平均情况下：每次遍历都需要进行部分比较和交换操作，时间复杂度为 O(n2)。

冒泡排序是一种稳定的排序算法。即相等的元素在排序后不会改变相对顺序。原因在于，当两个相邻的元素相等时，冒泡排序不会交换它们的位置，从而保持了相对顺序的稳定性。

3. 选择排序

选择排序（Selection Sort）是一种简单直观的排序算法。其基本思想是每一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，直到全部待排序的数据元素排完。虽然选择排序的时间复杂度较高，但其实现简单，适用于小规模数据的排序。

关于选择排序的具体步骤如下（按照升序描述）:

初始状态：将整个序列分为已排序区间和未排序区间。初始时已排序区间为空，未排序区间为整个序列。
选择最小值：在未排序区间中找到最小的元素。
交换位置：将这个最小元素和未排序区间的第一个元素交换位置，使其成为已排序区间的最后一个元素。
重复步骤：重复步骤2和步骤3，直到未排序区间为空。

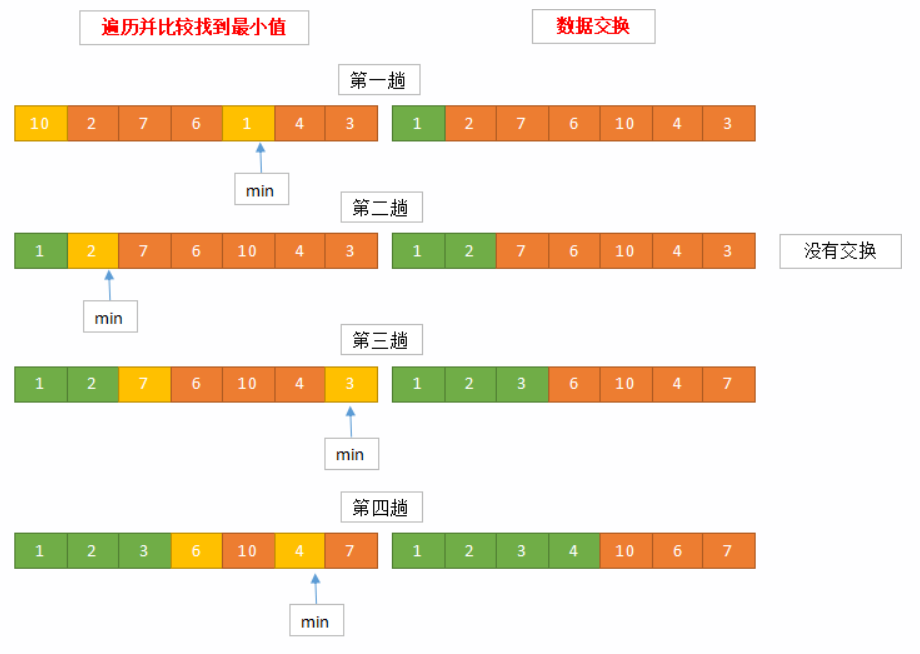
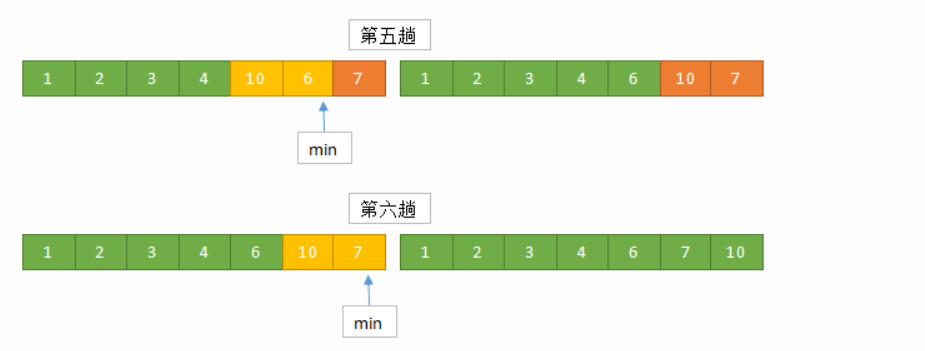
下面是使用C++编写的选择排序的示例代码:

#include <iostream>
#include <vector>
using namespace std;void selectionSort(vector<int>& vec)
{int size = vec.size();for (int i = 0; i < size - 1; ++i){int minPos = i; for (int j = i + 1; j < size; ++j){if (vec[j] < vec[minPos]) {minPos = j; }}if (minPos != i){swap(vec[i], vec[minPos]);}}
}int main()
{srand(time(NULL));vector<int> data;cout << "排序前的原始数据: ";for (int i = 0; i < 10; ++i){data.push_back(rand() % 100);cout << data.back() << " ";}cout << endl;selectionSort(data);cout << "排序之后的数据: ";for (const auto& item : data){cout << item << " ";}cout << endl;return 0;
}

选择排序的时间复杂度不受输入数据的初始状态影响，始终为 O(n2)。具体分析如下：

• 最坏情况下：每次选择最小元素都需要遍历未排序部分的所有元素，因此时间复杂度为 O(n2)。
• 最优情况下：即使输入数据已经有序，选择排序仍需遍历所有元素，因此时间复杂度依旧为 O(n2)。
• 平均情况下：每次选择最小元素的操作与最坏情况类似，时间复杂度为 O(n2)。
  选择排序是一种不稳定的排序算法。即相等的元素在排序后可能改变相对顺序。原因在于，当选择最小元素并进行交换时，可能会将相等元素的相对位置改变。例如，数组 [5, 3, 5, 2] 经过第一次选择后变为 [2, 3, 5, 5]，两个 5 的相对顺序发生了改变。

4. 插入排序

插入排序（Insertion Sort）是一种简单直观的排序算法。它的基本思想是将未排序部分的元素插入到已排序部分的适当位置，从而逐步构建有序列表。插入排序在小规模数据集和部分有序数据集上的表现较好，具有稳定性和简单性。

关于插入排序的具体步骤如下（按照升序描述）:

1. 初始化：从第二个元素（索引为1）开始，将其视为待插入元素。默认第一个元素是已经排好序的有序序列。
2. 遍历：从未排序部分的第一个元素开始，逐一将每个元素插入到已排序部分的适当位置。
3. 插入操作：
   • 将当前元素（称为“待插入元素”）与已排序部分的元素从后向前进行比较。
   • 如果已排序的元素大于待插入元素，则将该已排序元素向右移动一位。
   • 重复上述比较和移动操作，直到找到一个已排序元素小于或等于待插入元素的位置。
   • 将待插入元素插入到这个位置。

重复步骤2和步骤3，直到所有元素都排序完成。

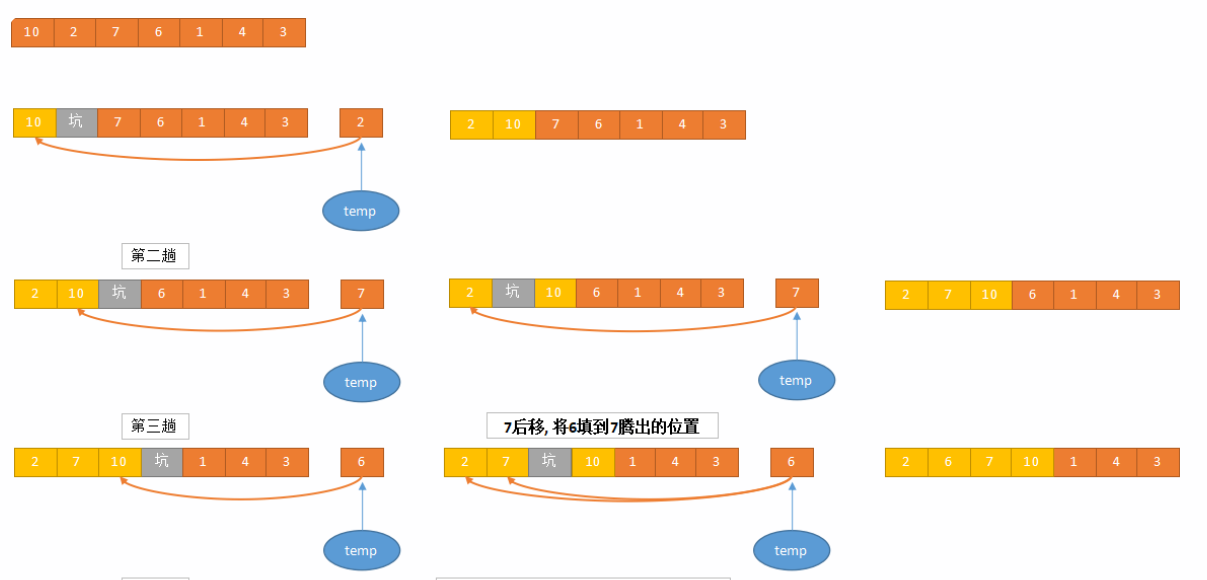
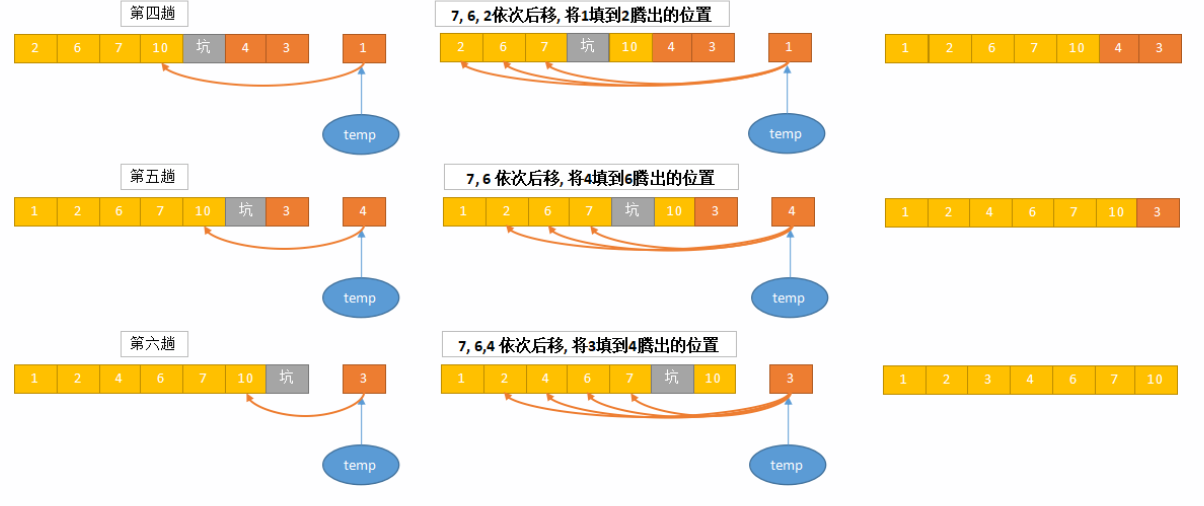
下面是使用C++编写的插入排序的示例代码:

#include <iostream>
#include <vector>
using namespace std;void insertionSort(vector<int>& vec)
{int size = vec.size();for (int i = 1; i < size; ++i){int key = vec[i];int j = i - 1;  while (j >= 0 && vec[j] > key){vec[j + 1] = vec[j];j--;}vec[j + 1] = key;}
}int main()
{srand(time(NULL));vector<int> data;cout << "排序前的原始数据: ";for (int i = 0; i < 10; ++i){data.push_back(rand() % 100);cout << data.back() << " ";}cout << endl;insertionSort(data);cout << "排序之后的数据: ";for (const auto& item : data){cout << item << " ";}cout << endl;return 0;
}

插入排序的时间复杂度取决于输入数组的初始状态：

• 最坏情况下：数组是反向排序的，需要进行最大次数的比较和移动操作，时间复杂度为 O(n2)。
• 最优情况下：数组已经有序，只需进行 n-1 次比较，时间复杂度为 O(n)。
• 平均情况下：需要进行部分比较和移动操作，时间复杂度为 O(n2)。

插入排序是一种稳定的排序算法。即相等的元素在排序后不会改变相对顺序。原因在于，当插入相等的元素时，只需插入到相等元素之后即可，不会改变其相对位置。

5. 希尔排序

希尔排序（Shell Sort）是插入排序的一种改进版本，旨在提高插入排序在大规模数据集上的效率。它通过将数据集分割成多个子序列分别进行插入排序，逐步减少子序列的间隔，最终在整个序列上进行插入排序，从而减少数据移动的次数，提升排序效率。

关于希尔排序的具体步骤如下（按照升序描述）:

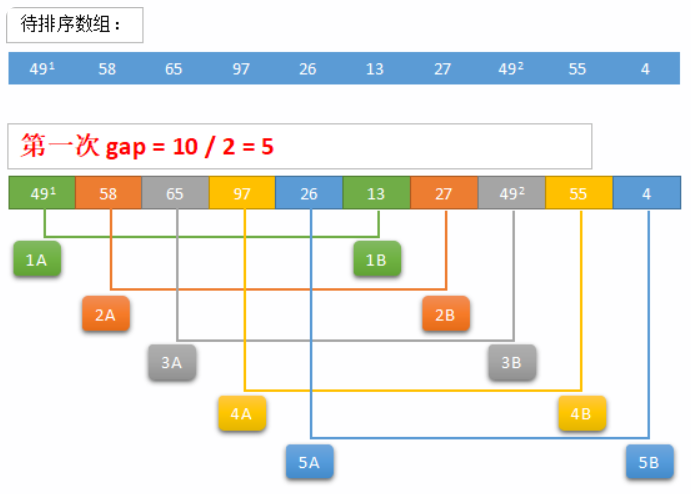
1. 选择初始增量序列：设置一个增量gap，常见的选择是初始增量为数组长度的一半，然后逐步减半，直到增量为1。也可以根据实际情况使用其他的增量（增量不同，排序的效率也不同）。
2. 对每个增量进行排序：
   • 分组：将数组分成多个子序列，子序列中的元素间隔为gap。
   • 对子序列进行插入排序：对每个子序列进行插入排序。由于gap较大，子序列的长度较短，插入排序效率较高。
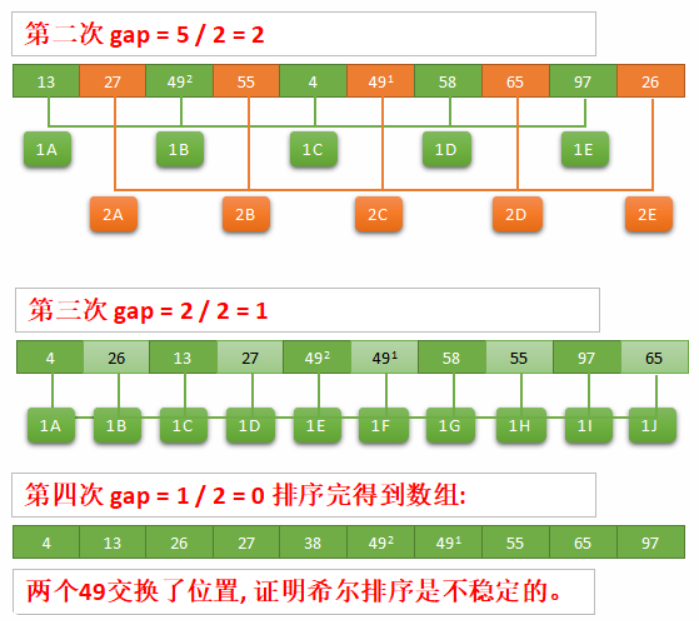
3. 重复步骤2：减小增量，继续对每个减小后的增量进行排序，直到增量为1。增量为1时，整个数组就是一个整体，进行一次标准的插入排序。

下面是使用C++编写的希尔排序的示例代码:

#include <iostream>
#include <vector>
using namespace std;void shellSort(vector<int>& vec)
{int size = vec.size();for (int gap = size / 2; gap > 0; gap /= 2){for (int i = gap; i < size; ++i){int temp = vec[i];int j = i - gap;while (j >= 0 && vec[j] > temp){vec[j + gap] = vec[j];j -= gap;}vec[j + gap] = temp;}}
}int main()
{srand(time(NULL));vector<int> data;cout << "排序前的原始数据: ";for (int i = 0; i < 10; ++i){data.push_back(rand() % 100);cout << data.back() << " ";}cout << endl;shellSort(data);cout << "排序之后的数据: ";for (const auto& item : data){cout << item << " ";}cout << endl;return 0;
}

希尔排序的时间复杂度依赖于间隔序列的选择：

• 最坏情况下：时间复杂度O(n^2)。
• 最优情况下：时间复杂度为 O(n)。
• 平均情况下：时间复杂 O(n^1.3)。

希尔排序是一种不稳定的排序算法。即相等的元素在排序后可能改变相对顺序。原因在于当使用较大间隔进行交换时，相等元素的相对顺序可能会被打乱。

6. 快速排序

快速排序（Quick Sort）是一种高效的比较排序算法，由C.A.R. Hoare在1960年提出。快速排序采用分治策略，通过递归地将数组分割成子数组来实现排序。其平均时间复杂度为 O(n log n)，在大多数情况下表现良好，因此在实际应用中广泛使用。

关于快速排序的具体步骤如下（按照升序描述）:

• 选择基准：从数组中选择一个元素作为基准（pivot）。常见的选择方式是选择第一个元素、最后一个元素或者中间元素。
• 分区操作：将数组中小于基准的元素移到基准的左边，大于基准的元素移到基准的右边。
• 递归排序：递归地对基准左边和右边的子数组进行步骤1和步骤2的操作。
• 合并结果：当递归完成时，数组就变成了有序的。

下面是使用C++编写的快速排序的示例代码:

#include <iostream>
#include <vector>
using namespace std;void quickSort(vector<int>& vec, int left, int right)
{// 递归结束的条件if (left >= right){return;}int pivot = vec[(left + right) / 2];int begin = left - 1, end = right + 1;while (begin < end){// 先移动再判断do{begin++;} while (vec[begin] < pivot);do{end--;} while (vec[end] > pivot);if (begin < end){swap(vec[begin], vec[end]);}}quickSort(vec, left, end);quickSort(vec, end + 1, right);
}int main()
{srand(time(NULL));vector<int> data;cout << "排序前的原始数据: ";for (int i = 0; i < 10; ++i){data.push_back(rand() % 100);cout << data.back() << " ";}cout << endl;quickSort(data, 0, data.size() - 1);cout << "排序之后的数据: ";for (const auto& item : data){cout << item << " ";}cout << endl;return 0;
}

快速排序的时间复杂度受基准选择的影响：

• 最坏情况下：如果每次选择的基准都是当前数组中的最小或最大值，则每次只能将一个元素放在正确的位置，时间复杂度为 O(n2)。这种情况在数组已经有序或逆序时可能出现。
• 最优情况下：每次选择的基准都能将数组平分，时间复杂度为 O(n log n)。
• 平均情况下：在多数情况下，快速排序的时间复杂度为 O(n log n)。

快速排序是一种不稳定的排序算法。即相等的元素在排序后可能改变相对顺序。原因在于分区操作中，可能会交换相等的元素，从而改变它们的相对位置。

7. 归并排序

归并排序（Merge Sort）是一种基于分治法的高效排序算法。它的基本思想是将数组分成两个子数组，分别进行排序，然后合并这两个有序子数组。归并排序的时间复杂度为 O(n log n)，且具有稳定性，因此在实际应用中广泛使用。

关于归并排序的具体步骤如下（按照升序描述）:

1. 分割数组：

• 如果数组的长度大于1，将数组从中间分割成两部分。
• 对每一部分再递归进行分割，直到每个子数组的长度为1。

2. 合并排序：

• 合并两个有序的子数组成一个有序的数组。
• 具体做法是比较两个子数组的第一个元素，将较小的元素放入合并结果中，并移到下一个元素，重复这个过程直到一个子数组为空，然后将另一个子数组剩下的元素全部放入合并结果中。

3. 递归合并：

• 对每个子数组重复上述步骤，直到所有子数组合并为一个完整的有序数组。

下面是使用C++编写的归并排序的示例代码:

#include <iostream>
#include <vector>
using namespace std;void mergeSort(vector<int>& vec, int left, int right)
{if (left >= right){return;}int mid = (left + right) / 2;mergeSort(vec, left, mid);mergeSort(vec, mid + 1, right);int k = 0; int i = left, j = mid + 1;vector<int> tmp;while (i <= mid && j <= right){if (vec[i] <= vec[j]){tmp.push_back(vec[i++]);}else{tmp.push_back(vec[j++]);}}while (i <= mid){tmp.push_back(vec[i++]);}while (j <= right){tmp.push_back(vec[j++]);}for (i = left, k = 0; i <= right; ++i){vec[i] = tmp[k++];}
}int main()
{srand(time(NULL));vector<int> data;cout << "排序前的原始数据: ";for (int i = 0; i < 10; ++i){data.push_back(rand() % 100);cout << data.back() << " ";}cout << endl;mergeSort(data, 0, data.size() - 1);cout << "排序之后的数据: ";for (const auto& item : data){cout << item << " ";}cout << endl;return 0;
}

归并排序的时间复杂度可以通过递归方程来分析：

• 最坏情况下：归并排序的时间复杂度为 O(n log n)，因为每次分割数组的操作都是对半分，递归深度为 log n，每层的合并操作时间复杂度为 O(n)。
• 最优情况下：时间复杂度同样为 O(n log n)，因为归并排序的过程与数组的初始顺序无关，始终需要进行分割和合并操作。
• 平均情况下：归并排序的时间复杂度也是 O(n log n)，因为它在任何情况下都需要进行相同数量的分割和合并操作。

8. 堆排序

堆排序（Heap Sort）是一种基于二叉堆数据结构的比较排序算法。堆排序利用堆这种数据结构的性质来实现排序，分为构建初始堆和反复从堆中取出最大元素（对于升序排序）两个主要步骤。堆排序的时间复杂度为 O(n log n)，且不需要额外的内存空间，因此在实际应用中非常有效。

二叉堆其实就是一棵完全二叉树

下面是使用C++编写的堆排序的示例代码:

#include <iostream>
#include <vector>
using namespace std;void heapAdjust(vector<int>& vec, int len, int parent)
{int largest = parent;int left = 2 * parent + 1;int right = 2 * parent + 2;if (left < len && vec[left] > vec[largest]){largest = left;}if (right < len && vec[right] > vec[largest]){largest = right;}if (largest != parent){swap(vec[parent], vec[largest]);heapAdjust(vec, len, largest);}
}void heapSort(vector<int>& vec)
{int size = vec.size();for (int i = size / 2 - 1; i >= 0; --i){heapAdjust(vec, vec.size(), i);}for (int i = size - 1; i > 0; --i){swap(vec[0], vec[i]);heapAdjust(vec, i, 0);}
}int main()
{srand(time(NULL));vector<int> data;cout << "排序前的原始数据: ";for (int i = 0; i < 11; ++i){data.push_back(rand() % 100);cout << data.back() << " ";}cout << endl;heapSort(data);cout << "排序之后的数据: ";for (const auto& item : data){cout << item << " ";}cout << endl;return 0;
}

堆排序的时间复杂度可以通过以下分析得出：

• 最坏情况下：构建最大堆的时间复杂度为 O(n)，每次调整堆的时间复杂度为 O(log n)，因此总时间复杂度为 O(n log n)。
• 最优情况下：时间复杂度同样为 O(n log n)，因为无论数组初始状态如何，都需要进行构建堆和调整堆的操作。
• 平均情况下：堆排序的时间复杂度也是 O(n log n)，与数组初始状态无关。

堆排序是一种不稳定的排序算法。即相等的元素在排序后可能改变相对顺序。原因在于堆的调整过程中，可能会交换相等元素的位置，从而改变它们的相对顺序。

9. 基数排序

基数排序（Radix Sort）是一种非比较排序算法，通过逐位处理数字来排序数组。它利用桶排序的思想，对数字的每一位进行排序，从最低有效位到最高有效位。基数排序特别适用于处理大量的整数或字符串数据。其时间复杂度为 O(d*(n+k))，其中 d 是数字的位数，n 是数组的长度，k 是基数【使用十进制，基数 ( k = 10 )】。
关于基数排序的具体步骤如下（按照升序描述）:

1. 确定排序的最大位数：

• 找出数组中最大数的位数 k，作为基数排序的迭代次数。

2. 按每一位进行计数排序：

• 从最低位到最高位（从个位到最高位），对数组进行排序。
• 使用桶排序作为子过程，根据当前位的数值对元素进行排序。
  • 根据数据的范围和分布创建若干个桶，每个桶负责一定范围内的数值。
  • 根据每个元素的值，将其分配到对应的桶中
  • 依次遍历每个桶，即完成了基于当前数字位的排序，并使用它覆盖原来的数据序列
• 使用新的数据序列进行下一轮的桶排序。

下面是使用C++编写的基数排序的示例代码:

#include <iostream>
#include <vector>
#include <string>
using namespace std;void radixSort(vector<int>& vec)
{int max = 0;for (int i = 0; i < vec.size(); ++i){if (max < vec[i]){max = vec[i];}}int len = to_string(max).length(); vector<vector<int>> bucket;int mod = 10, dev = 1;for (int i = 0; i < len; ++i, mod *= 10, dev *= 10){bucket.resize(10);  // 有10个桶: 0~9for (int j = 0; j < vec.size(); ++j){int num = vec[j] % mod / dev;bucket[num].push_back(vec[j]);}int index = 0;for (const auto& item : bucket){for (const auto& it : item){vec[index++] = it;}}bucket.clear();}
}int main()
{srand(time(NULL));vector<int> data;cout << "排序前的原始数据: ";for (int i = 0; i < 10; ++i){data.push_back(rand() % 100);cout << data.back() << " ";}cout << endl;radixSort(data);cout << "排序之后的数据: ";for (const auto& item : data){cout << item << " ";}cout << endl;return 0;
}

基数排序的时间复杂度可以通过以下分析得出：

• 最坏情况下：时间复杂度为 O(d*(n+k))，其中 d 是最大数的位数，n 是数组的大小，k 是基数。
• 最优情况下：时间复杂度同样为 O(d*(n+k))，因为无论数组初始状态如何，都需要对每一位进行排序。
• 平均情况下：基数排序的时间复杂度也是 O(d*(n+k))。

总结

算法	平均时间复杂度	最好时间复杂度	最坏时间复杂度	空间复杂度	稳定性
冒泡排序	O(n2)	O(n)	O(n2)	O(1)	稳定
选择排序	O(n2)	O(n2)	O(n2)	O(1)	不稳定
插入排序	O(n2)	O(n)	O(n2)	O(1)	稳定
希尔排序	O(n1.3)	O(n)	O(n2)	O(1)	不稳定
快速排序	O(n log n)	O(n log n)	O(n2)	O(log n)	不稳定
归并排序	O(n log n)	O(n log n)	O(n log n)	O(n)	稳定
堆排序	O(n log n)	O(n log n)	O(n log n)	O(1)	不稳定
基数排序	O(d*(n+k))	O(d*(n+k))	O(d*(n+k))	O(n+k)	稳定

三者在 STL 中的协同工作 (Introsort)

template <typename RandomIt>
void sort(RandomIt first, RandomIt last) {// 递归深度限制：2 * log2(n)const int depth_limit = 2 * log2(last - first);// 1. 内省排序主循环（快排+堆排）introsort(first, last, depth_limit);// 2. 最终插入排序（处理小数组）insertion_sort(first, last);
}void introsort(RandomIt first, RandomIt last, int depth) {// 小数组跳过if (last - first <= 16) return;// 深度超限转堆排序if (depth == 0) {heap_sort(first, last);return;}// 快排分区auto pivot = median_of_three(*first, *(first+(last-first)/2), *(last-1));auto [left, right] = partition(first, last, pivot);// 尾递归优化introsort(first, left, depth - 1);introsort(right, last, depth - 1);
}

算法对比表

特性	快速排序	堆排序	插入排序
时间复杂度	平均 O(n log n)，最坏 O(n²)	最坏 O(n log n)	平均 O(n²)，最佳 O(n)
空间复杂度	O(log n) 递归栈	O(1) 原地	O(1) 原地
稳定性	通常不稳定	不稳定	稳定
适用场景	通用大规模数据	需要最坏情况保证	小数据或基本有序数据
缓存友好性	中等（分区访问）	差（跳转访问）	优秀（顺序访问）
STL 使用场景	主要排序引擎	深度超限时使用	小数组最终排序

性能实测参考（10万 int 排序）

算法	随机数据(ms)	升序数据(ms)	降序数据(ms)
快速排序	12	2100（退化）	2200（退化）
堆排序	25	24	26
插入排序	>5000	2	4
STL sort	10	8	9

|注：STL 的 Introsort 在各类数据上都保持高效