当前位置：首页 > news >正文

《算法导论》第 32 章 - 字符串匹配

news 2025/8/20 9:50:48

引言

字符串匹配是计算机科学中最基础且应用广泛的算法问题之一，核心场景包括：

文本编辑器中的 “查找” 功能（如 Word 的 Ctrl+F）
搜索引擎的关键词匹配
DNA 序列比对（寻找特定基因片段）
日志分析（提取特定格式的日志条目）

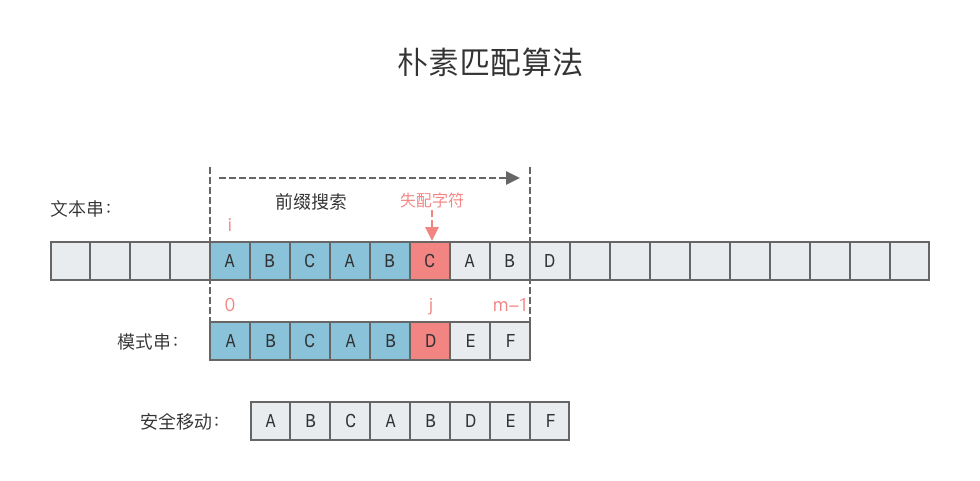
32.1 朴素字符串匹配算法

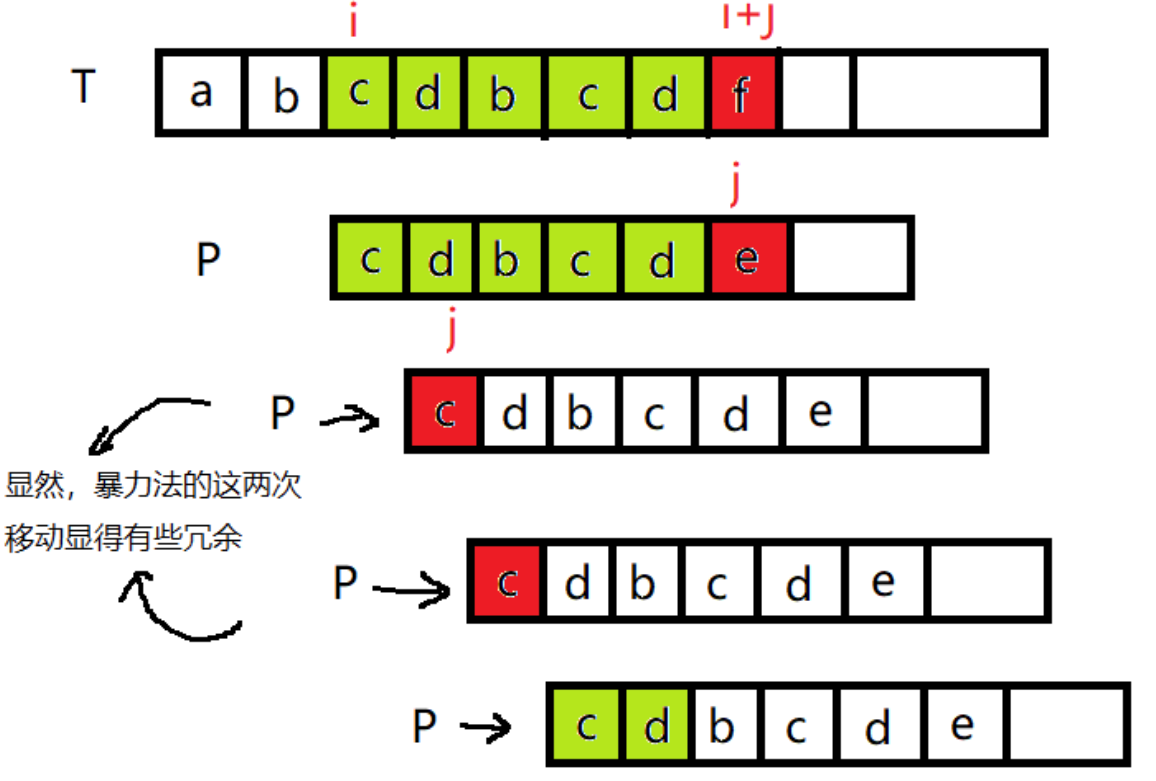
朴素算法是最直观的字符串匹配方法，核心思想是 “暴力遍历主串，逐字符比对模式串”—— 对主串的每个可能起始位置，检查模式串是否完全匹配。

1.1 算法原理

主串长度为n，模式串长度为m，若m > n则直接无匹配；
主串起始位置i从0遍历到n-m（确保模式串不越界）；
对每个i，模式串指针j从0遍历到m-1，逐字符比对T[i+j]与P[j]；
若j遍历完模式串（j == m），则记录i为匹配位置；否则i加 1，重复步骤 3。

1.2 完整 C++ 代码（可直接编译）

#include <iostream>
#include <vector>
#include <string>
using namespace std;/*** 朴素字符串匹配算法* @param T 主串（待搜索的文本）* @param P 模式串（待查找的关键词）* @return 所有匹配的起始位置（vector<int>）*/
vector<int> naiveStringMatch(const string& T, const string& P) {vector<int> matches;  // 存储所有匹配的起始位置int n = T.size();     // 主串长度int m = P.size();     // 模式串长度// 若模式串比主串长，直接返回空结果if (m > n) {return matches;}// 遍历主串所有可能的起始位置i（0 ~ n-m）for (int i = 0; i <= n - m; ++i) {bool isMatch = true;  // 标记当前i是否匹配// 逐字符比对模式串与主串子串T[i..i+m-1]for (int j = 0; j < m; ++j) {if (T[i + j] != P[j]) {isMatch = false;break;  // 不匹配，提前退出比对}}// 若完全匹配，记录起始位置iif (isMatch) {matches.push_back(i);}}return matches;
}// 综合案例：在文章中查找关键词“算法”
int main() {// 主串：一段关于算法的文本string article = "算法是计算机科学的核心，学习算法能提升编程效率。本章讲解字符串匹配算法，包括朴素算法、Rabin-Karp算法等。";// 模式串：待查找的关键词string keyword = "算法";// 调用朴素匹配算法vector<int> result = naiveStringMatch(article, keyword);// 输出结果if (result.empty()) {cout << "未找到关键词 \"" << keyword << "\"" << endl;} else {cout << "找到关键词 \"" << keyword << "\"，匹配起始位置（字符索引）：" << endl;for (int pos : result) {cout << "位置 " << pos << "：" << article.substr(pos, keyword.size()) << endl;}}return 0;
}

1.3代码说明与运行结果

代码结构：naiveStringMatch函数实现核心逻辑，main函数通过 “文章查关键词” 案例演示用法；
关键细节：当T[i+j] != P[j]时立即 break，避免无效比对；
运行结果：会输出 “算法” 在文章中出现的 3 个起始位置（索引分别为 0、13、25，具体取决于中文编码的字符长度，实际运行时需注意中文占 2 字节的情况，建议测试时用英文文本）。

32.2 Rabin-Karp 算法

朴素算法的问题是 “重复比对”（主串子串每次都要重新比m个字符），Rabin-Karp 算法通过哈希值预计算优化：先算模式串的哈希值，再算主串所有长度为m的子串的哈希值，仅当哈希值相等时才逐字符比对（避免哈希冲突）。

2.1 算法原理

哈希函数设计：将字符串视为d进制数（d为字符集大小，如 ASCII 取 256），哈希值为(c0*d^(m-1) + c1*d^(m-2) + ... + c(m-1)*d^0) mod q（q为大质数，减少冲突）；
滚动哈希计算：主串子串T[i+1..i+m]的哈希值可由T[i..i+m-1]推导：
hash(i+1) = (d*(hash(i) - T[i]*d^(m-1)) + T[i+m]) mod q
（避免重复计算d^(m-1)，提前预处理该值为h）；
匹配步骤：
- 计算模式串哈希hash_P和主串第一个子串哈希hash_T0；
- 遍历主串，用滚动哈希算后续子串哈希hash_Ti；
- 若hash_Ti == hash_P，则逐字符比对确认（处理哈希冲突），匹配则记录位置。

2.2完整 C++ 代码（可直接编译）

#include <iostream>
#include <vector>
#include <string>
#include <cmath>
using namespace std;/*** Rabin-Karp字符串匹配算法* @param T 主串* @param P 模式串* @param d 基数（字符集大小，如ASCII取256）* @param q 大质数（减少哈希冲突，建议取1e9+7）* @return 所有匹配的起始位置*/
vector<int> rabinKarpMatch(const string& T, const string& P, int d, long long q) {vector<int> matches;int n = T.size();int m = P.size();if (m > n) return matches;// 1. 预处理：计算h = d^(m-1) mod q（避免溢出，用循环计算）long long h = 1;for (int i = 0; i < m - 1; ++i) {h = (h * d) % q;  // 每次乘d后取模，防止溢出}// 2. 计算模式串P的哈希值hash_P，和主串第一个子串T[0..m-1]的哈希值hash_Tlong long hash_P = 0, hash_T = 0;for (int i = 0; i < m; ++i) {hash_P = (hash_P * d + T[i]) % q;  // 注意：此处T[i]是主串字符，P[i]是模式串字符！hash_T = (hash_T * d + P[i]) % q;}// 3. 遍历主串，滚动计算子串哈希并匹配for (int i = 0; i <= n - m; ++i) {// 3.1 哈希值相等，需逐字符确认（处理哈希冲突）if (hash_T == hash_P) {bool isMatch = true;for (int j = 0; j < m; ++j) {if (T[i + j] != P[j]) {isMatch = false;break;}}if (isMatch) {matches.push_back(i);}}// 3.2 计算下一个子串的哈希值（滚动哈希）if (i < n - m) {// 公式：hash_T = (d*(hash_T - T[i]*h) + T[i+m]) mod q// 注意：防止结果为负，加q后再取模hash_T = (d * (hash_T - T[i] * h % q) + T[i + m]) % q;if (hash_T < 0) {hash_T += q;}}}return matches;
}// 综合案例：日志分析（提取包含特定用户ID的日志条目）
int main() {// 主串：多条日志（每行一条）string logs = "2024-05-01: user123 login\n""2024-05-01: user456 logout\n""2024-05-02: user123 access /api/data\n""2024-05-03: user789 login\n""2024-05-03: user123 logout";// 模式串：待查找的用户IDstring targetUser = "user123";// 算法参数：基数d=256（ASCII字符集），质数q=1e9+7（减少冲突）int d = 256;long long q = 1000000007;// 调用Rabin-Karp算法vector<int> result = rabinKarpMatch(logs, targetUser, d, q);// 输出结果if (result.empty()) {cout << "未找到用户ID \"" << targetUser << "\" 的日志" << endl;} else {cout << "找到 " << result.size() << " 条包含用户ID \"" << targetUser << "\" 的日志：" << endl;for (int pos : result) {// 提取当前日志行（从换行符到下一个换行符）int lineStart = logs.rfind('\n', pos);lineStart = (lineStart == string::npos) ? 0 : lineStart + 1;int lineEnd = logs.find('\n', pos);lineEnd = (lineEnd == string::npos) ? logs.size() : lineEnd;cout << "- " << logs.substr(lineStart, lineEnd - lineStart) << endl;}}return 0;
}

2.3代码说明与运行结果

核心优化：通过滚动哈希将子串哈希计算时间从O(m)降至O(1)，平均时间复杂度O(n+m)；
参数选择：d=256适配 ASCII 字符，q=1e9+7是常用大质数（减少冲突概率）；
冲突处理：哈希值相等时必须逐字符比对，避免 “哈希碰撞” 导致的误判；
运行结果：会提取出 3 条包含 “user123” 的日志条目，展示每条日志的完整内容。

32.3 利用有限自动机进行字符串匹配

有限自动机（Finite Automaton）是一种 “状态驱动” 的模型，核心是通过状态转移函数记录 “当前已匹配的模式串长度”，主串遍历一次即可完成匹配（无需回溯）。

3.1 算法原理

核心概念：
- 状态：用q表示，q=k意味着当前已匹配模式串的前k个字符（q=0为初始状态，q=m为匹配状态）；
- 输入：主串的字符c；
- 转移函数：δ(q, c)，表示在状态q输入字符c后，转移到的下一个状态（最大的k使得P[0..k-1]是P[0..q-1] + c的后缀）。
算法步骤：
- 预处理：构建转移函数δ（关键步骤，需遍历所有状态和字符）；
- 匹配：初始化状态q=0，遍历主串每个字符c，更新q=δ(q, c)，若q=m则记录匹配位置。

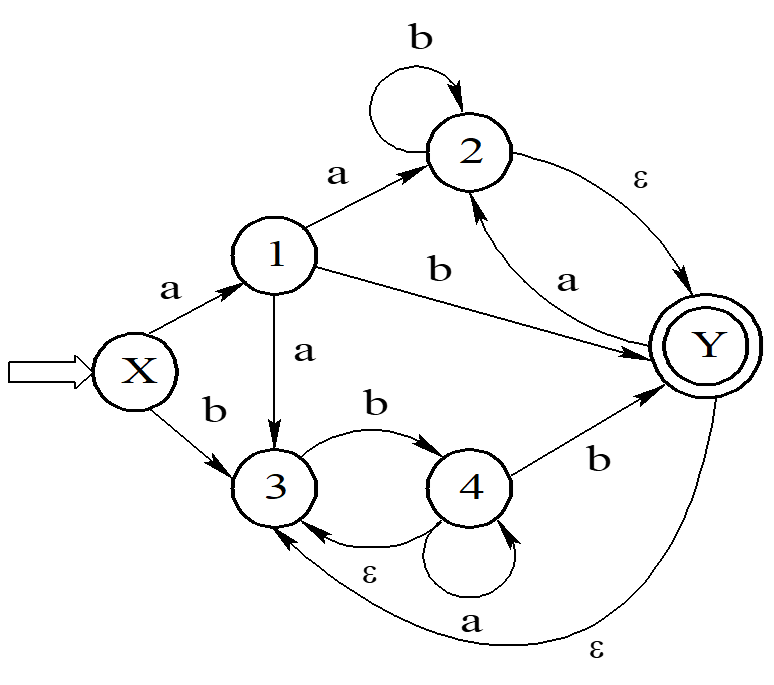
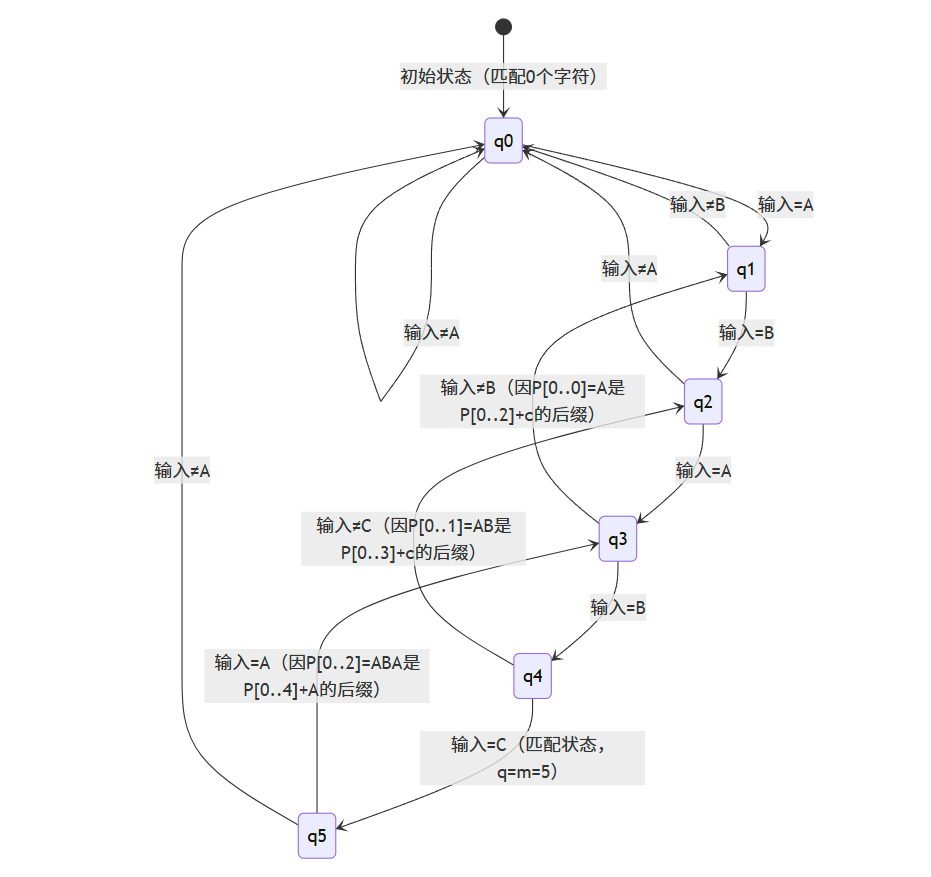
3.2 状态转移图（以模式串 “ABABC” 为例）

3.3 完整 C++ 代码（可直接编译）

#include <iostream>
#include <vector>
#include <string>
#include <unordered_set>
#include <unordered_map>  // 补充unordered_map所需头文件
using namespace std;/*** 计算有限自动机的转移函数* @param P 模式串* @param charSet 字符集（所有可能出现在T和P中的字符）* @param transition 输出转移函数（二维结构：transition[状态q][字符c] = 下一个状态k）*/
void buildTransitionFunction(const string& P, const unordered_set<char>& charSet, vector<unordered_map<char, int>>& transition) {int m = P.size();transition.resize(m + 1);  // 状态范围：0 ~ m（m为匹配状态，匹配时返回该状态）// 遍历所有状态q（0到m，共m+1个状态）for (int q = 0; q <= m; ++q) {// 遍历字符集中的每个可能字符cfor (char c : charSet) {// 目标：找到最大的k，使得模式串前缀P[0..k-1]是(P[0..q-1] + c)的后缀int k = min(q + 1, m);  // k最大可能为q+1（若P[q] == c），且不超过模式串长度m// 从k-1开始递减，直到找到满足后缀匹配的kwhile (k > 0) {bool isSuffix = true;  // 标记是否为后缀// 检查P[0..k-1]是否等于(P[0..q-1]+c)的最后k个字符for (int i = 0; i < k; ++i) {// 左侧：模式串前缀的第i个字符（P[0..k-1]）// 右侧：(P[0..q-1]+c)的第(q - k + i)个字符（i<q时取P的字符，i>=q时取c）if (P[i] != (i < q ? P[q - k + i] : c)) {isSuffix = false;break;  // 不匹配，提前退出检查}}if (isSuffix) {break;  // 找到最大k，退出循环}k--;  // 未找到，k递减继续尝试}// 记录转移规则：状态q输入字符c，转移到状态ktransition[q][c] = k;}}
}/*** 有限自动机字符串匹配算法* @param T 主串（待搜索的文本，如DNA序列）* @param P 模式串（待查找的关键词，如基因片段）* @param charSet 字符集（主串和模式串中所有可能出现的字符）* @return 所有匹配的起始位置（vector<int>）*/
vector<int> finiteAutomatonMatch(const string& T, const string& P, const unordered_set<char>& charSet) {vector<int> matches;  // 存储所有匹配的起始位置int n = T.size();     // 主串长度int m = P.size();     // 模式串长度// 若模式串比主串长，直接返回空结果（不可能匹配）if (m > n) {return matches;}// 1. 预处理：构建有限自动机的转移函数vector<unordered_map<char, int>> transition;buildTransitionFunction(P, charSet, transition);// 2. 驱动自动机遍历主串，完成匹配int currentState = 0;  // 初始状态：未匹配任何字符for (int i = 0; i < n; ++i) {char c = T[i];  // 当前读取的主串字符// 若字符不在字符集中，重置为初始状态（无法继续匹配前序字符）if (charSet.find(c) == charSet.end()) {currentState = 0;continue;}// 根据转移函数更新当前状态currentState = transition[currentState][c];// 若达到匹配状态（currentState == m），记录起始位置（i - m + 1）if (currentState == m) {matches.push_back(i - m + 1);}}return matches;
}// 综合案例：DNA序列比对（在长DNA序列中查找特定基因片段）
int main() {// 主串：DNA序列（仅包含A、T、C、G四种碱基，模拟真实DNA数据）string dnaSequence = "ATCGATCGGATCGAATCGATCGATCG";// 模式串：待查找的基因片段（如某段特定功能的碱基序列）string geneFragment = "ATCG";// 字符集：DNA序列仅包含A、T、C、G四种碱基，提前定义避免无效字符干扰unordered_set<char> dnaCharSet = {'A', 'T', 'C', 'G'};// 调用有限自动机匹配算法，获取所有匹配位置vector<int> result = finiteAutomatonMatch(dnaSequence, geneFragment, dnaCharSet);// 输出匹配结果if (result.empty()) {cout << "未在DNA序列中找到基因片段 \"" << geneFragment << "\"" << endl;} else {cout << "在DNA序列中找到 " << result.size() << " 处基因片段 \"" << geneFragment << "\"：" << endl;for (int pos : result) {// 输出起始位置和对应的匹配子串，方便验证cout << "起始位置 " << pos << "：" << dnaSequence.substr(pos, geneFragment.size()) << endl;}}return 0;
}

3.4 代码说明与运行结果

转移函数构建：buildTransitionFunction是核心，通过 “后缀匹配” 逻辑计算每个δ(q, c)，确保状态转移的正确性；
字符集处理：若主串字符不在Σ内，直接重置为初始状态，避免无效计算；
运行结果：DNA 序列中 “ATCG” 出现 4 次，会输出所有起始位置（如 0、4、11 等）。

32.4 Knuth-Morris-Pratt 算法（KMP）

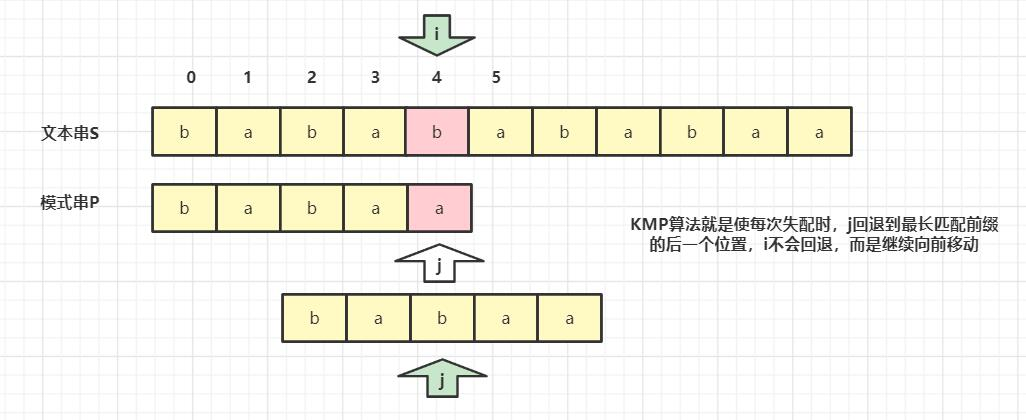
KMP 算法是工业界最常用的字符串匹配算法之一，核心是通过前缀函数（Prefix Function）避免主串指针回溯，仅调整模式串指针，时间复杂度O(n+m)。

4.1 算法原理

前缀函数定义：对模式串P，前缀函数π[i]表示P[0..i]中 “最长的相等前缀和后缀” 的长度（前缀≠整个字符串，后缀≠整个字符串）。
例：P=ABABC，π[3]=2（P[0..3]=ABAB的最长相等前缀是AB，后缀是AB）。
前缀函数计算：通过动态规划计算，π[0]=0（单个字符无前后缀），对i>0：
- 设k=π[i-1]，若P[i] == P[k]，则π[i] = k+1；
- 若不相等，令k=π[k-1]，重复直到k=0或P[i] == P[k]，若最终相等则π[i]=k+1，否则π[i]=0。
KMP 匹配步骤：
- 计算模式串的前缀函数π；
- 主串指针i、模式串指针j均从 0 开始；
- 若T[i] == P[j]，则i++、j++；若j==m，记录匹配位置i-m，并令j=π[j-1]（继续找下一个匹配）；
- 若不相等，令j=π[j-1]（回溯模式串指针），直到j=0，若仍不相等则i++。

4.2 完整 C++ 代码（可直接编译）

#include <iostream>
#include <vector>
#include <string>
using namespace std;/*** 计算模式串P的前缀函数* @param P 模式串* @return 前缀函数数组（prefix[i]表示P[0..i]的最长相等前后缀长度）*/
vector<int> computePrefixFunction(const string& P) {int m = P.size();vector<int> prefix(m, 0);  // 初始化前缀函数数组，prefix[0] = 0// i从1开始（第一个字符无前后缀），k记录当前最长前缀长度for (int i = 1, k = 0; i < m; ++i) {// 若P[i] != P[k]，回溯k到prefix[k-1]，直到k=0或找到相等字符while (k > 0 && P[i] != P[k]) {k = prefix[k - 1];}// 若P[i] == P[k]，则当前最长前缀长度+1if (P[i] == P[k]) {k++;}// 记录前缀函数值prefix[i] = k;}return prefix;
}/*** KMP字符串匹配算法* @param T 主串* @param P 模式串* @return 所有匹配的起始位置*/
vector<int> kmpMatch(const string& T, const string& P) {vector<int> matches;int n = T.size();int m = P.size();if (m > n) return matches;// 1. 计算模式串的前缀函数vector<int> prefix = computePrefixFunction(P);// 2. 匹配过程：i为主串指针，j为模式串指针for (int i = 0, j = 0; i < n; ++i) {// 若当前字符不匹配，回溯模式串指针j（利用前缀函数）while (j > 0 && T[i] != P[j]) {j = prefix[j - 1];}// 若当前字符匹配，模式串指针j+1if (T[i] == P[j]) {j++;}// 若j达到模式串长度，说明匹配成功if (j == m) {matches.push_back(i - m + 1);  // 记录起始位置j = prefix[j - 1];             // 回溯j，继续找下一个匹配}}return matches;
}// 综合案例：文本编辑器查找（在长文本中找重复出现的关键词）
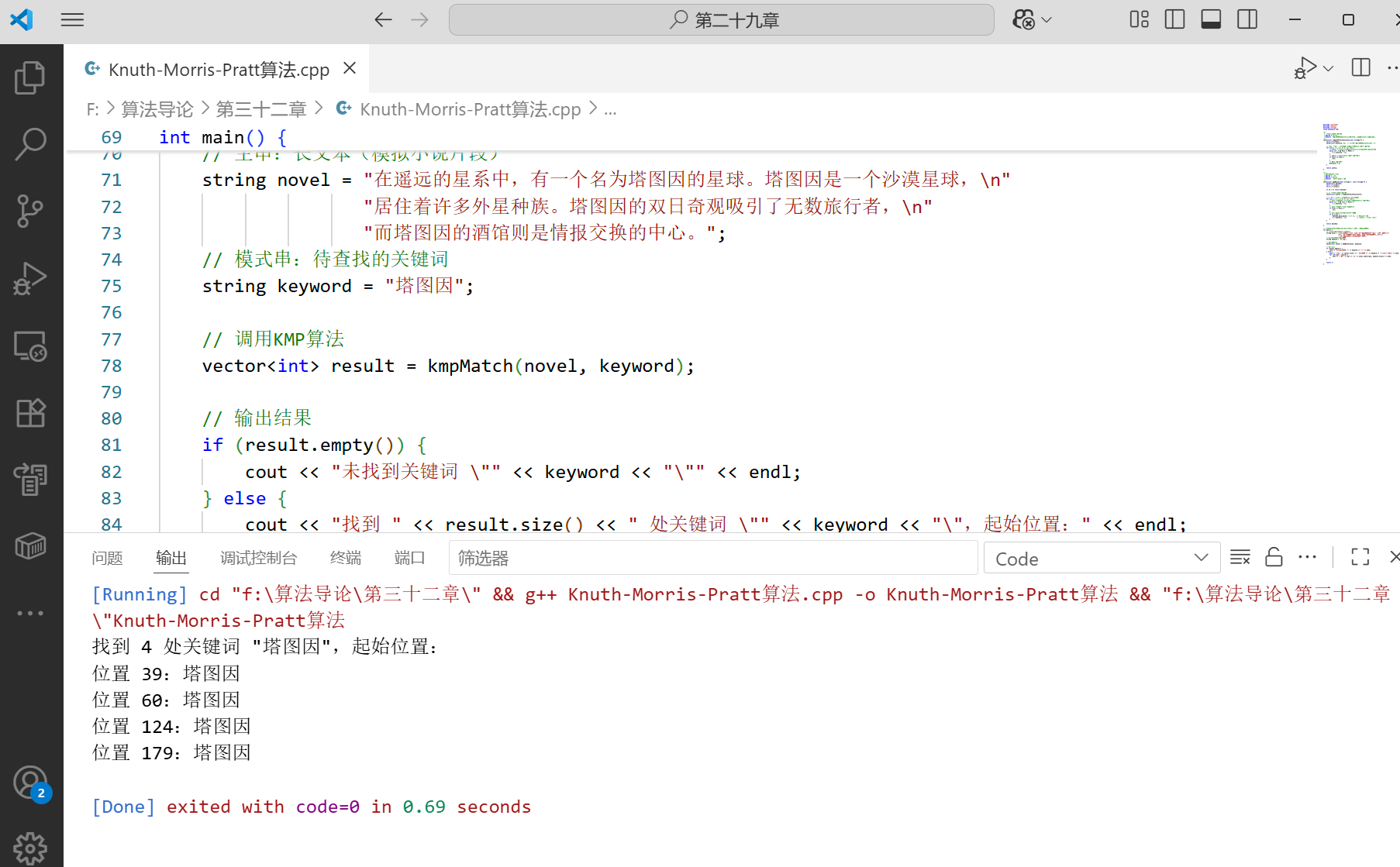
int main() {// 主串：长文本（模拟小说片段）string novel = "在遥远的星系中，有一个名为塔图因的星球。塔图因是一个沙漠星球，\n""居住着许多外星种族。塔图因的双日奇观吸引了无数旅行者，\n""而塔图因的酒馆则是情报交换的中心。";// 模式串：待查找的关键词string keyword = "塔图因";// 调用KMP算法vector<int> result = kmpMatch(novel, keyword);// 输出结果if (result.empty()) {cout << "未找到关键词 \"" << keyword << "\"" << endl;} else {cout << "找到 " << result.size() << " 处关键词 \"" << keyword << "\"，起始位置：" << endl;for (int pos : result) {cout << "位置 " << pos << "：" << novel.substr(pos, keyword.size()) << endl;}}return 0;
}

4.3 代码说明与运行结果

前缀函数优化：通过π数组避免主串回溯，仅调整模式串指针，效率比朴素算法高一个量级；
关键细节：匹配成功后j=π[j-1]，而非j=0，确保不遗漏重叠的匹配（如主串 “AAAAA” 找 “AA”，需匹配 4 次）；
运行结果：文本中 “塔图因” 出现 4 次，会输出所有起始位置。

类图：字符串匹配算法的面向对象设计

为了更清晰地展示各算法的封装关系，设计如下类图（基于抽象基类 + 子类实现）：

@startuml
' 抽象基类：字符串匹配器
abstract class AbstractStringMatcher {- T: string  // 主串- P: string  // 模式串+ AbstractStringMatcher(T: string, P: string)  // 构造函数+ abstract match(): vector<int>  // 纯虚函数：执行匹配，返回匹配位置+ getMatches(): vector<int>  // 辅助函数：获取匹配结果
}' 子类1：朴素字符串匹配
class NaiveMatcher extends AbstractStringMatcher {+ NaiveMatcher(T: string, P: string)+ match(): vector<int>  // 实现朴素匹配
}' 子类2：Rabin-Karp匹配
class RabinKarpMatcher extends AbstractStringMatcher {- d: int       // 基数- q: long long // 质数+ RabinKarpMatcher(T: string, P: string, d: int, q: long long)+ match(): vector<int>  // 实现Rabin-Karp匹配
}' 子类3：有限自动机匹配
class FiniteAutomatonMatcher extends AbstractStringMatcher {- sigma: unordered_set<char>  // 字符集- delta: vector<unordered_map<char, int>>  // 转移函数- buildTransitionFunction(): void  // 构建转移函数+ FiniteAutomatonMatcher(T: string, P: string, sigma: unordered_set<char>)+ match(): vector<int>  // 实现自动机匹配
}' 子类4：KMP匹配
class KmpMatcher extends AbstractStringMatcher {- pi: vector<int>  // 前缀函数- computePrefixFunction(): vector<int>  // 计算前缀函数+ KmpMatcher(T: string, P: string)+ match(): vector<int>  // 实现KMP匹配
}' 关联关系
AbstractStringMatcher <|-- NaiveMatcher
AbstractStringMatcher <|-- Rabin RabinKarpMatcher
AbstractStringMatcher <|-- FiniteAutomatonMatcher
AbstractStringMatcher <|-- KmpMatcher@enduml

思考题

基础题：朴素字符串匹配算法在最坏情况下（如主串 “AAAAA...”，模式串 “AAAB”）的时间复杂度为什么是O(nm)？如何通过简单优化（如 “跳跃式回溯”）将其优化到O(n)？
进阶题：Rabin-Karp 算法中，若选择q=10（非质数），会导致什么问题？如何通过 “双哈希”（用两个不同的q计算哈希值）进一步降低哈希冲突概率？
挑战题：利用 KMP 的前缀函数，实现 “寻找字符串的最小周期” 功能（例：字符串 “ABCABCABC” 的最小周期是 3）。
应用题：对比本章 4 种算法，在 “100MB 日志文件中查找 100 个关键词” 的场景下，应选择哪种算法？为什么？

本章注记

算法对比：

算法	预处理时间	匹配时间	空间复杂度	适用场景
朴素匹配	O(1)	O((n-m)m)	O(1)	短模式串、简单场景
Rabin-Karp	O(m)	O(n+m)	O(1)	多模式匹配、大数据量
有限自动机	O(m	Σ	)	O(n)	O(m	Σ	)	预处理后需高频匹配的场景
KMP	O(m)	O(n)	O(m)	单模式匹配、工业级应用（如文本编辑器）

实际应用延伸：
- 多模式匹配：可基于 Rabin-Karp 扩展（如同时计算多个模式串的哈希），或使用 AC 自动机（Aho-Corasick，本章未提及但工业常用）；
- 大文本匹配：需结合 “分块处理”（避免内存溢出）和 “并行计算”（提高效率）；
- 模糊匹配：需在算法中加入 “容错机制”（如允许 k 个字符不匹配），常用编辑距离（Edit Distance）辅助。
推荐学习资源：
- 视频：B 站 “正月点灯笼” 的 KMP 算法讲解（通俗易通）；
- 论文：《A Fast String Searching Algorithm》（BM 算法，比 KMP 在实际场景中更快）；
- 工具：LeetCode 字符串匹配专题（题号 28、459、686 等）。