当前位置：首页 > news >正文

机器学习-决策树：从原理到实战的机器学习入门指南

news 2025/8/19 10:38:37

在机器学习的众多算法中，决策树以其直观易懂、可解释性强的特点，成为入门者的理想选择。它模拟人类决策过程，通过层层判断实现分类或回归任务。本文将从基本概念、核心原理到实战案例，全面解析决策树的工作机制。

一、决策树的基本概念

决策树：是一种树形结构的监督学习算法，其核心逻辑是 “从根节点开始一步步走到叶子节点”。所有数据最终都会落到叶子节点，这一特性使它既能处理分类问题，也能完成回归任务。

一棵完整的决策树由三部分组成：

根节点：整个树的第一个选择点，是决策的起点。

非叶子节点与分支：中间决策过程，每个非叶子节点代表一次特征判断，分支则对应判断结果。

叶子节点：最终的决策结果，所有到达该节点的数据都会被赋予这个结果。

例如，在 “是否去聚会” 的决策树中，根节点可能是 “有没有聚会”，分支为 “是” 或 “否”；非叶子节点可能是 “作业要交”，分支为 “接近”“否”“紧急”；而 “去酒吧”“学习”“看电视” 等则是叶子节点。

二、决策树的训练与测试流程

训练阶段

训练的目标是从给定的训练集中构造出一棵决策树，关键在于从根节点开始选择特征并进行特征切分。

测试阶段

一旦决策树构造完成，测试过程就变得简单。只需将测试数据从根节点开始，按照树的分支规则一步步向下走，最终到达的叶子节点就是预测结果。

三、特征切分的核心：熵与信息增益

1.熵：衡量不确定性的指标

熵：熵是表示随机变量不确定性的度量。

公式：H(X)=- ∑ pi * logpi, i=1,2, ... , n

例子： A集合[1,1,1,1,1,1,1,1,2,2] B集合[1,2,3,4,5,6,7,8,9,1]

其中pi是第i类别的概率。熵值越大，说明数据的不确定性越高：

1.当p=0或p=1时，H(p)=0，此时随机变量完全没有不确定性（所有数据属于同一类别）。

2.当p=0.5时，H(p)=1，随机变量的不确定性最大（两类数据各占一半）。

例如，集合A=[1,1,1,1,1,1,1,1,2,2]中，1 出现的概率为 0.8，2 出现的概率为 0.2，熵值较低；而集合B=[1,2,3,4,5,6,7,8,9,1]包含多种类别，不确定性更高，熵值也更大。在分类任务中，我们希望通过节点分支后，数据类别的熵值更小，即同类数据更集中。

2.信息增益：选择最优特征的标准

信息增益表示特征X使得类Y的不确定性减少的程度，它等于分支前的熵减去分支后的加权平均熵。信息增益越大，说明该特征对降低数据不确定性的作用越明显，也就越适合作为当前节点的切分特征。

四、决策树构造实例

以 “14 天打球情况” 数据集为例，我们来具体看看决策树的构造过程。该数据集包含 14 天的打球记录，特征为 4 种环境变化（outlook、temperature、humidity、windy），目标是构造一棵判断 “是否打球” 的决策树。

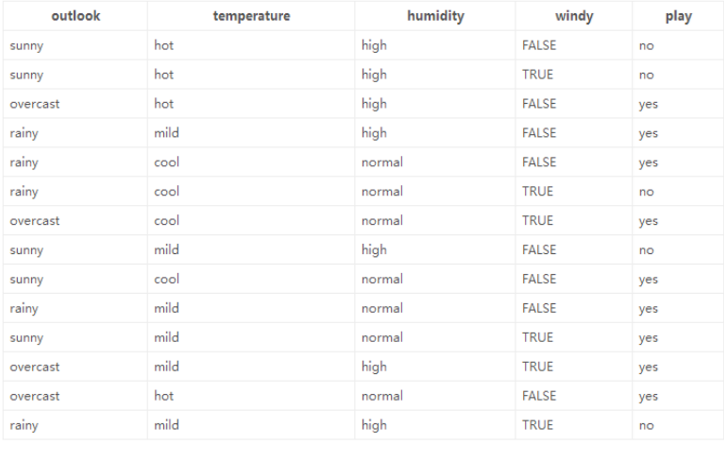
初始熵计算

14 天中有 9 天打球，5 天不打球，初始熵值为H=−(149log149+145log145)≈0.940。

特征信息增益计算

我们逐一计算每个特征的信息增益：

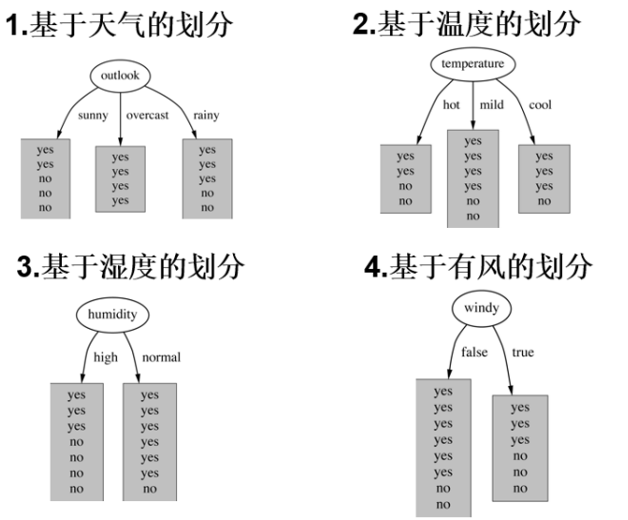
1.对于 outlook 特征，其取值为 sunny、overcast、rainy 的概率分别为 5/14、4/14、5/14。对应的熵值分别为 0.971、0、0.971。分支后的加权平均熵为5/14×0.971+4/14×0+5/14×0.971≈0.693，信息增益为0.940−0.693=0.247。

2.用同样的方法计算其他特征的信息增益，选择信息增益最大的 outlook 作为根节点。