[优选算法专题二滑动窗口——水果成篮]
题目链接
904. 水果成篮 - 力扣(LeetCode)
题目描述

题目解析
问题深入理解
题解思路
首先分析一下题目的意思:
你拥有两个篮子,每个篮子可以放一种水果
我们需要以某一棵树为起点,连续摘下每棵树的果子,要求尽可能摘多的果子,注意:题目要求必须连续采摘
当我们遇到第三种水果时,摘果结束
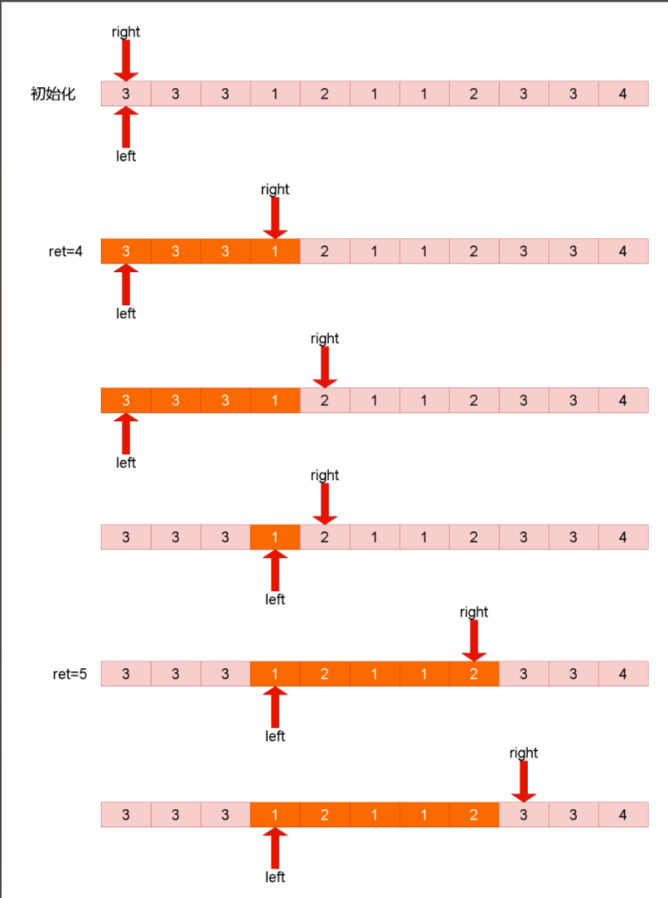
eg: [0,1,2,2]
一共有三种水果,分别是:0,1,2号水果
当我们从下标为0 的地方开始采摘,那么可以采摘【0,1】,一共可以采摘两个水果
当我们从下标为1 的地方开始采摘,那么可以采摘【1,2,2】,一共可以采摘三个水果
问题本质
"水果成篮" 问题本质上是一个滑动窗口经典应用,可以抽象为:
在一个数组中,寻找最长的连续子数组,该子数组最多最多包含两种不同元素。
这属于 "最多包含 k 种元素的最长子数组" 问题的特例(k=2)。
算法原理:滑动窗口(Sliding Window)
核心思想
滑动窗口是一种在数组或链表上高效遍历子序列的技术,通过维护一个 "窗口"(由左右两个指针界定的连续区间),动态调整窗口大小来寻找满足条件的解。
对于本问题:
- 窗口需要满足的条件:最多包含 2 种水果类型
- 优化目标:窗口的长度尽可能大
算法工作原理
- 初始化窗口:左右指针
left和right都从 0 开始,形成一个初始窗口[0,0]- 扩展窗口:向右移动
right指针,将新元素纳入窗口- 维护窗口合法性:当窗口中元素类型超过 2 种时,向右移动
left指针,直到窗口重新满足条件- 记录最优解:每次调整后计算当前窗口长度,更新最大长度
这个过程就像一个滑动的窗口在数组上移动,不断扩大右边界,必要时收缩左边界,始终保持窗口的合法性,同时追踪最大窗口长度。
如下图
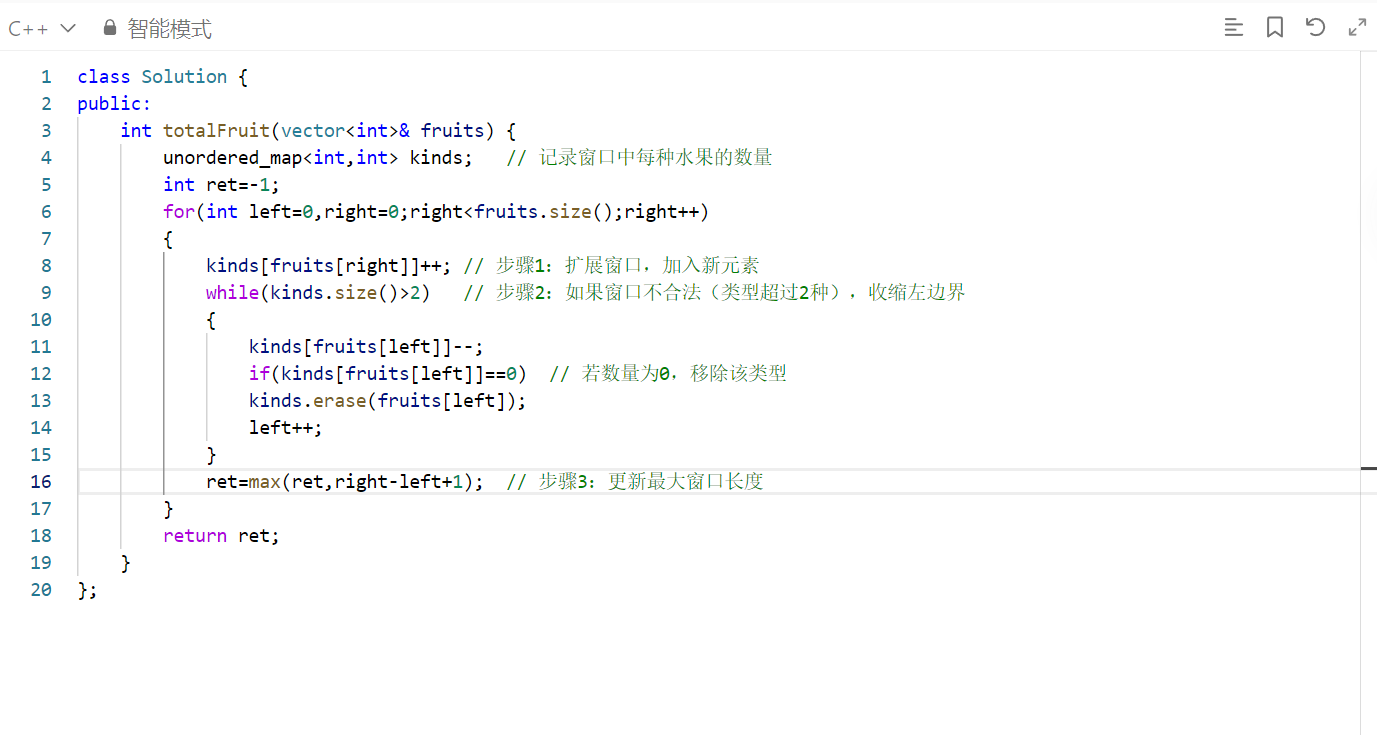
完整代码
算法特性分析
时间复杂度:O(n)
- 每个元素最多被
left和right指针各访问一次- 哈希表的操作(插入、删除、查找)都是 O (1)
空间复杂度:O(1)
- 哈希表最多存储 3 种水果类型(调整窗口时可能短暂出现 3 种)
- 额外变量仅占用常数空间

