python自学笔记9 Seaborn可视化

Seaborn：统计可视化利器

作为基于 Matplotlib 的高级绘图库，有一下功能：

一元特征数据

直方图

import matplotlib.pyplot as plt 
import pandas as pd  
import seaborn as sns # import os
# # 如果文件夹不存在，创建文件夹
# if not os.path.isdir("Figures"):
#     os.makedirs("Figures")# 导入鸢尾花数据
iris_sns = sns.load_dataset("iris") iris_sns# 绘制花萼长度样本数据直方图
fig, ax = plt.subplots(figsize = (8, 6))sns.histplot(data=iris_sns, x="sepal_length", binwidth=0.2, ax = ax)								# 纵轴三个选择：频率、概率、概率密度ax.axvline(x = iris_sns.sepal_length.mean(), color = 'r', ls = '--')								# 增加均值位置竖直参考线# 参考https://seaborn.pydata.org/tutorial/distributions.html

效果：


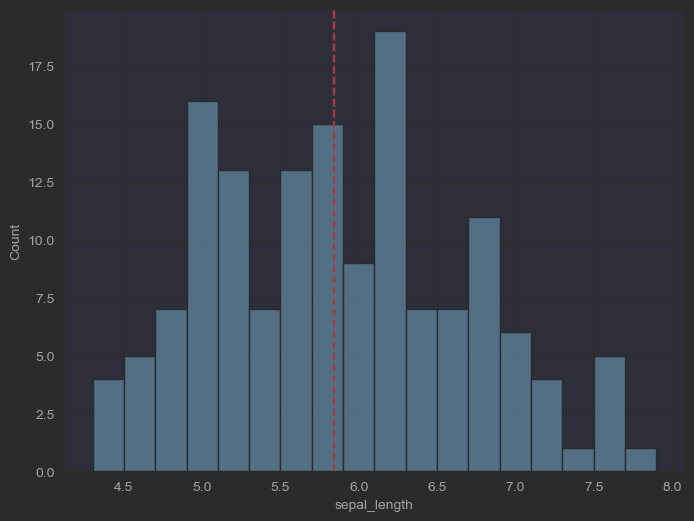
代码演示如下图所示：

# 绘制花萼长度样本数据直方图， 考虑鸢尾花分类
fig, ax = plt.subplots(figsize = (8,6))
sns.histplot(data = iris_sns, x="sepal_length",
hue = 'species', binwidth=0.2, ax = ax,
element="step", stat = 'density')
# 纵轴为概率密度

如果要分组的话使用如下代码：

fig, ax = plt.subplots(figsize=(8, 6))
sns.histplot(data=iris_sns,          # 数据源（DataFrame）x="sepal_length",       # 指定x轴为花萼长度hue='species',          # 按鸢尾花种类分组着色binwidth=0.2,           # 直方图条柱宽度为0.2ax=ax,                  # 指定绘图坐标轴element="step",         # 直方图样式为阶梯线stat='density'          # 纵轴显示密度而非计数
)

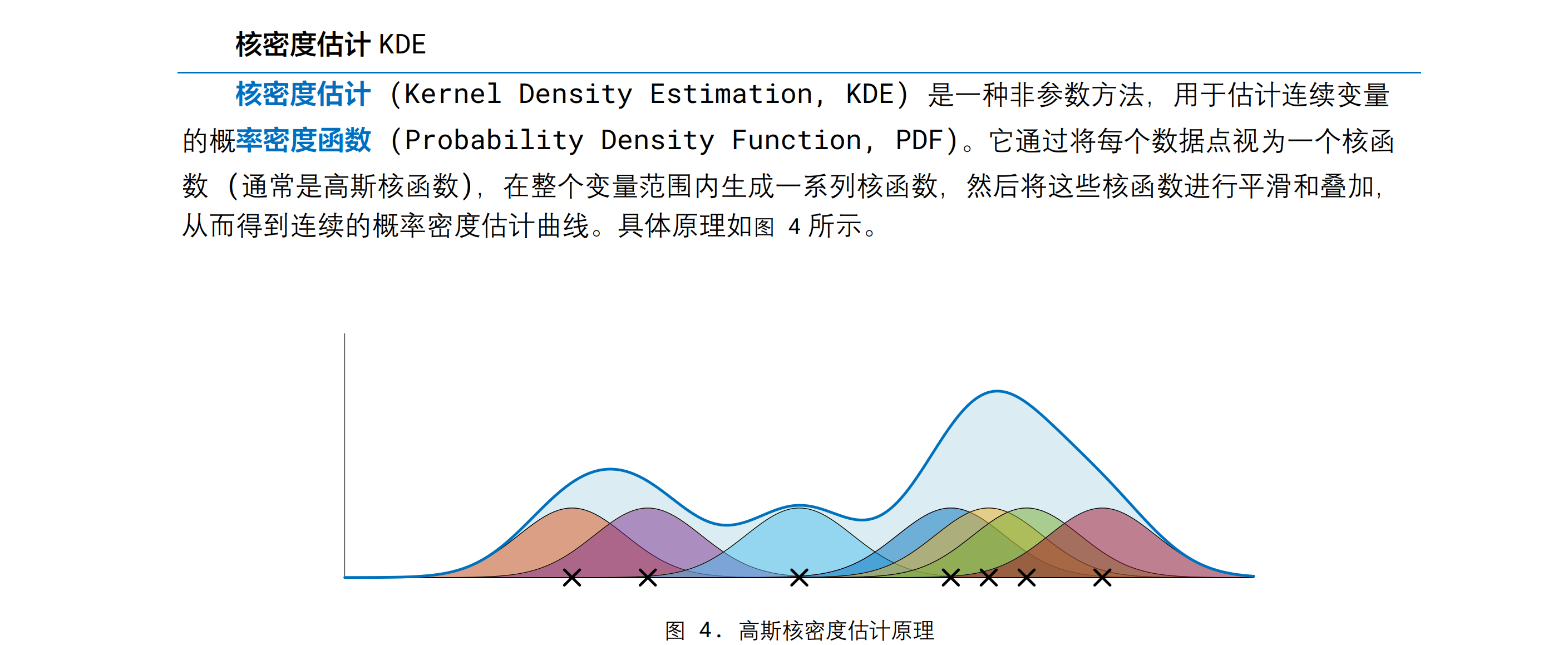
核密度估计KDE

将每个点变成一个高斯核函数（就是高斯分布的那个函数形式），然后再叠加

# 绘制花萼长度样本数据，高斯核密度估计
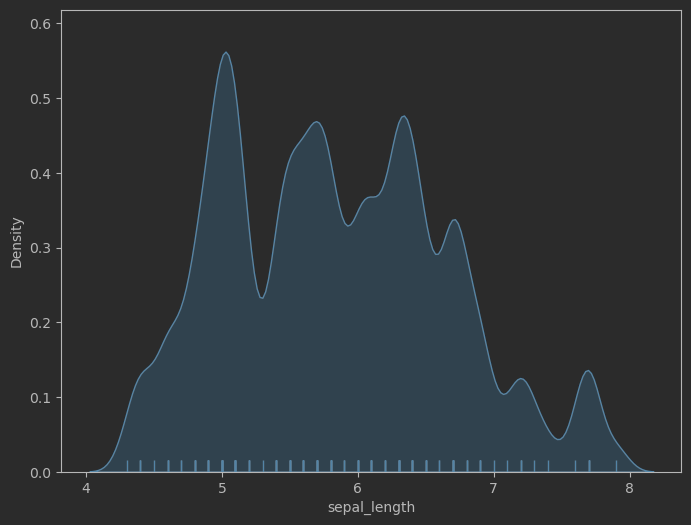
fig, ax = plt.subplots(figsize = (8,6))sns.kdeplot(data=iris_sns, x="sepal_length", 	# 生成核密度曲线bw_adjust=0.3, fill = True)			# 调整曲率，填充区域
sns.rugplot(data=iris_sns, x="sepal_length")	# 生产毛毯图（小刺）

效果：

# 绘制花萼长度样本数据，高斯核密度估计，考虑鸢尾花类别
fig, ax = plt.subplots(figsize = (8,6))sns.kdeplot(data=iris_sns, x="sepal_length", hue = 'species', # 各自的分布bw_adjust=0.5, fill = True)
sns.rugplot(data=iris_sns, x="sepal_length", hue = 'species')# fig.savefig('Figures\一元，kdeplot + rugplot + hue.svg', format='svg')

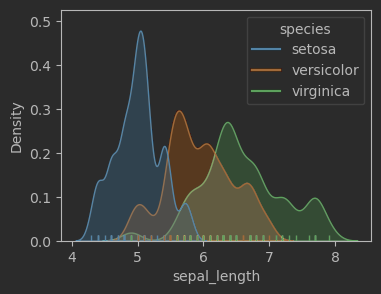
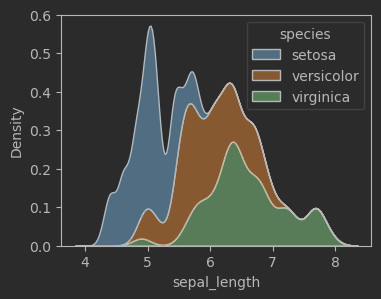
# 绘制花萼长度样本数据，高斯核密度估计，考虑鸢尾花类别，堆叠
fig, ax = plt.subplots(figsize = (8,6))sns.kdeplot(data=iris_sns, x="sepal_length", hue="species", multiple="stack", 		# 设置叠加属性bw_adjust=0.5)

效果：

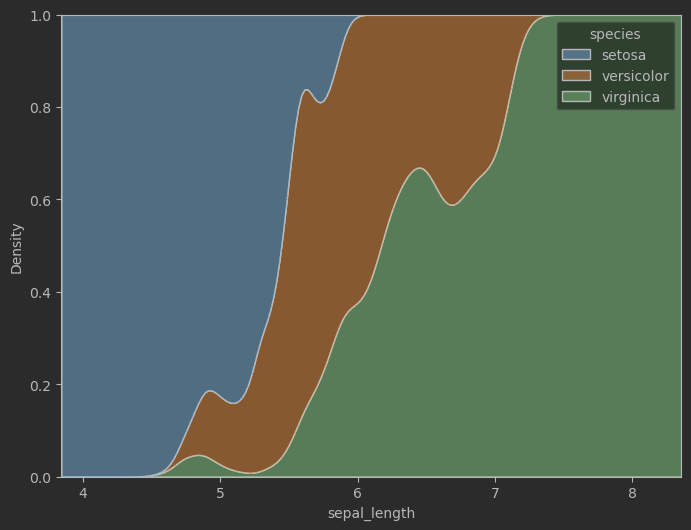
# 绘制后验概率 (成员值)fig, ax = plt.subplots(figsize = (8,6))
sns.kdeplot(data=iris_sns, x="sepal_length", hue="species", bw_adjust=0.5,multiple = 'fill')			# 设置叠加效果

效果：

分散点图/蜂群图

较小的数据使用：seaborn.stripplot() 蜂群图
较大的数据使用：seaborn.swarmplot() 分散点图

# 绘制鸢尾花花萼长度分散点图
fig, ax = plt.subplots(figsize = (8,6))
sns.stripplot(data=iris_sns, x="sepal_length", y="species", hue="petal_length", palette="RdYlBu_r", ax = ax)

效果：

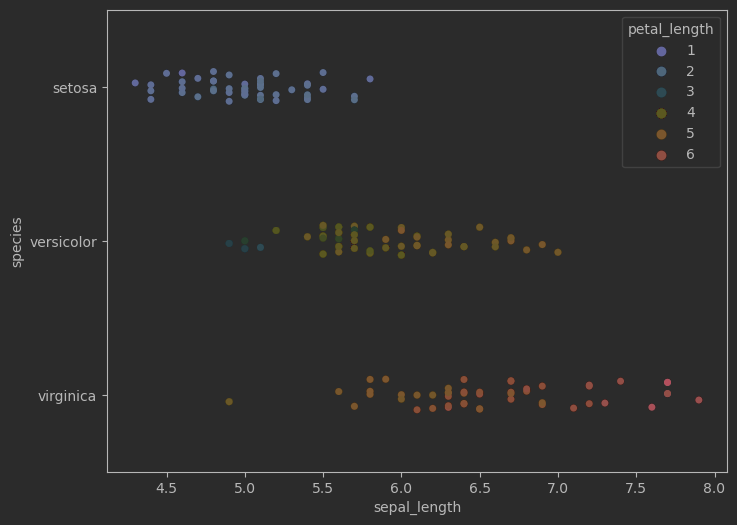
# 绘制花萼长度样本数据， 蜂群图
fig, ax = plt.subplots(figsize = (8,4))
sns.swarmplot(data=iris_sns, x="sepal_length", ax = ax)
# 绘制花萼长度样本数据， 蜂群图， 考虑分类
fig, ax = plt.subplots(figsize = (8,4))
sns.swarmplot(data=iris_sns, x="sepal_length", y = 'species',
hue = 'species', ax = ax)

箱型图

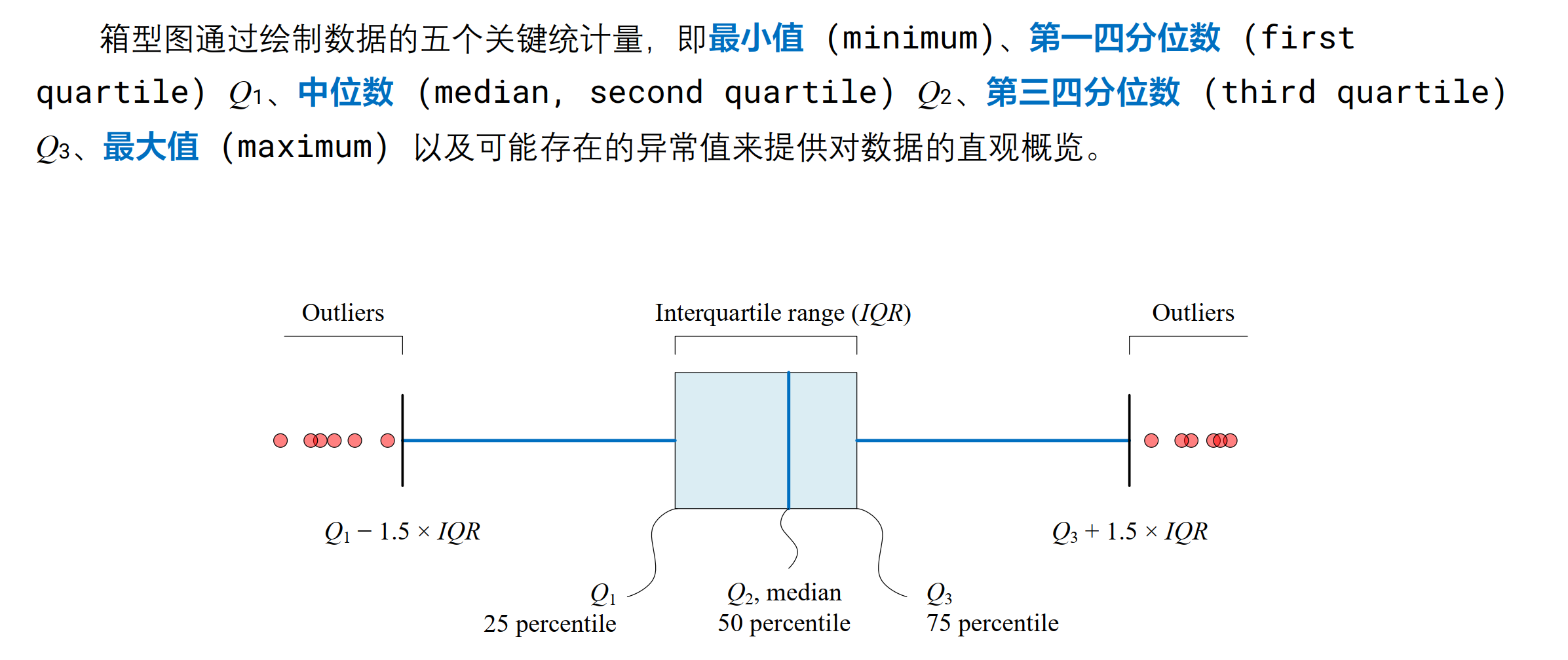
包含元素：

# 绘制鸢尾花花萼长度箱型图
fig, ax = plt.subplots(figsize = (8,2))
sns.boxplot(data=iris_sns, x="sepal_length", ax = ax)

效果：

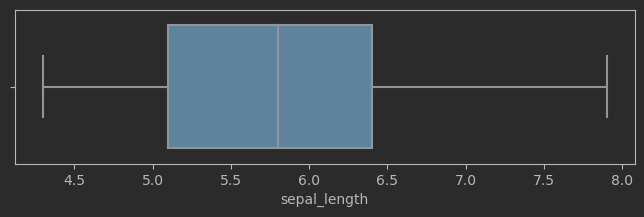
# 绘制鸢尾花花萼长度箱型图，考虑鸢尾花分类
fig, ax = plt.subplots(figsize = (8,3))
sns.boxplot(data=iris_sns, x="sepal_length", y = 'species', ax = ax)

效果：

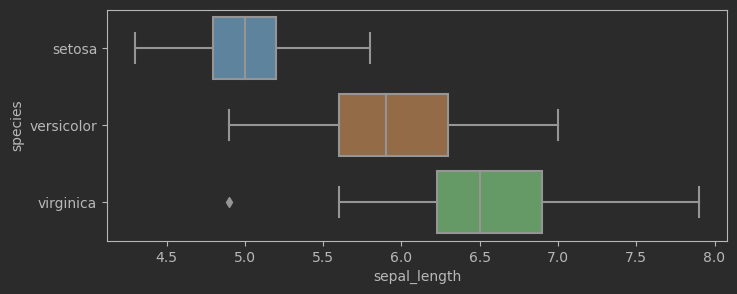
小提琴图

可以看成用核密度曲线优化的箱线图

# 绘制花萼长度样本数据，小提琴图
fig, ax = plt.subplots(figsize = (8,2))
sns.violinplot(data=iris_sns, x="sepal_length", ax = ax)

效果：

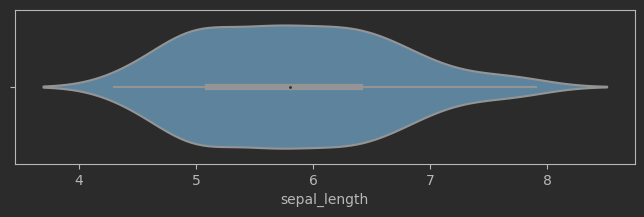
# 绘制花萼长度样本数据，小提琴图，考虑分类
fig, ax = plt.subplots(figsize = (8,4))
sns.violinplot(data=iris_sns, x="sepal_length", y="species", ax = ax)

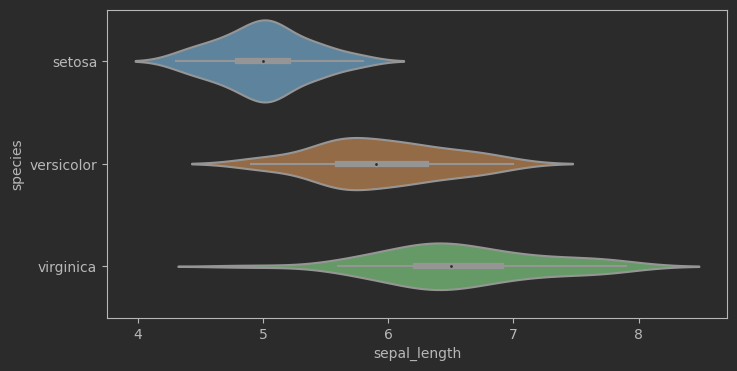
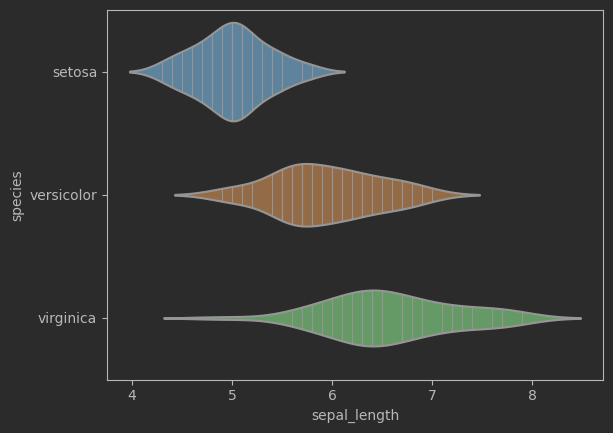
sns.violinplot(data=iris_sns, x="sepal_length", y="species", inner = 'stick')

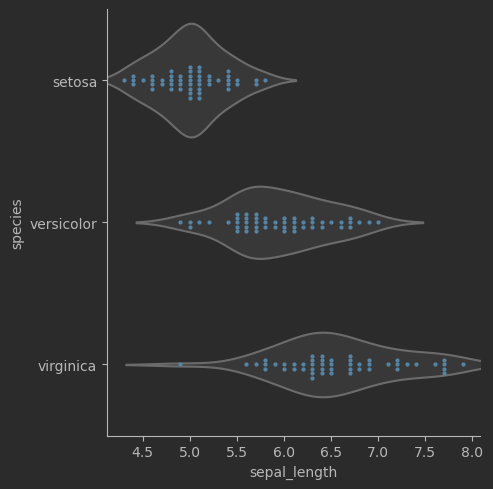
# 蜂群图 + 小提琴图，考虑鸢尾花分类sns.catplot(data=iris_sns, x="sepal_length", y="species", kind="violin", color=".9", inner=None)sns.swarmplot(data=iris_sns, x="sepal_length", y="species", size=3)

二元特征数据

散点图

通过散点图可以简要查看两个维度是否有何关系

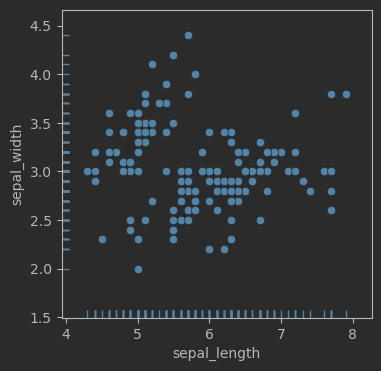
# 鸢尾花散点图 + 毛毯图
fig, ax = plt.subplots(figsize = (4,4))sns.scatterplot(data=iris_sns, x="sepal_length", y="sepal_width")
sns.rugplot(data=iris_sns, x="sepal_length", y="sepal_width")

效果：

fig, ax = plt.subplots(figsize = (4,4))sns.scatterplot(data=iris_sns, x="sepal_length", y="sepal_width", hue = 'species')
sns.rugplot(data=iris_sns, x="sepal_length", y="sepal_width", hue = 'species')fig.savefig('Figures\二元，scatterplot + rugplot + hue.svg', format='svg')

效果：

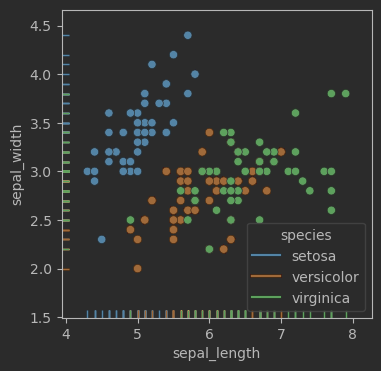
二元直方热图

二维散点图转化为直方图后效果并不清晰


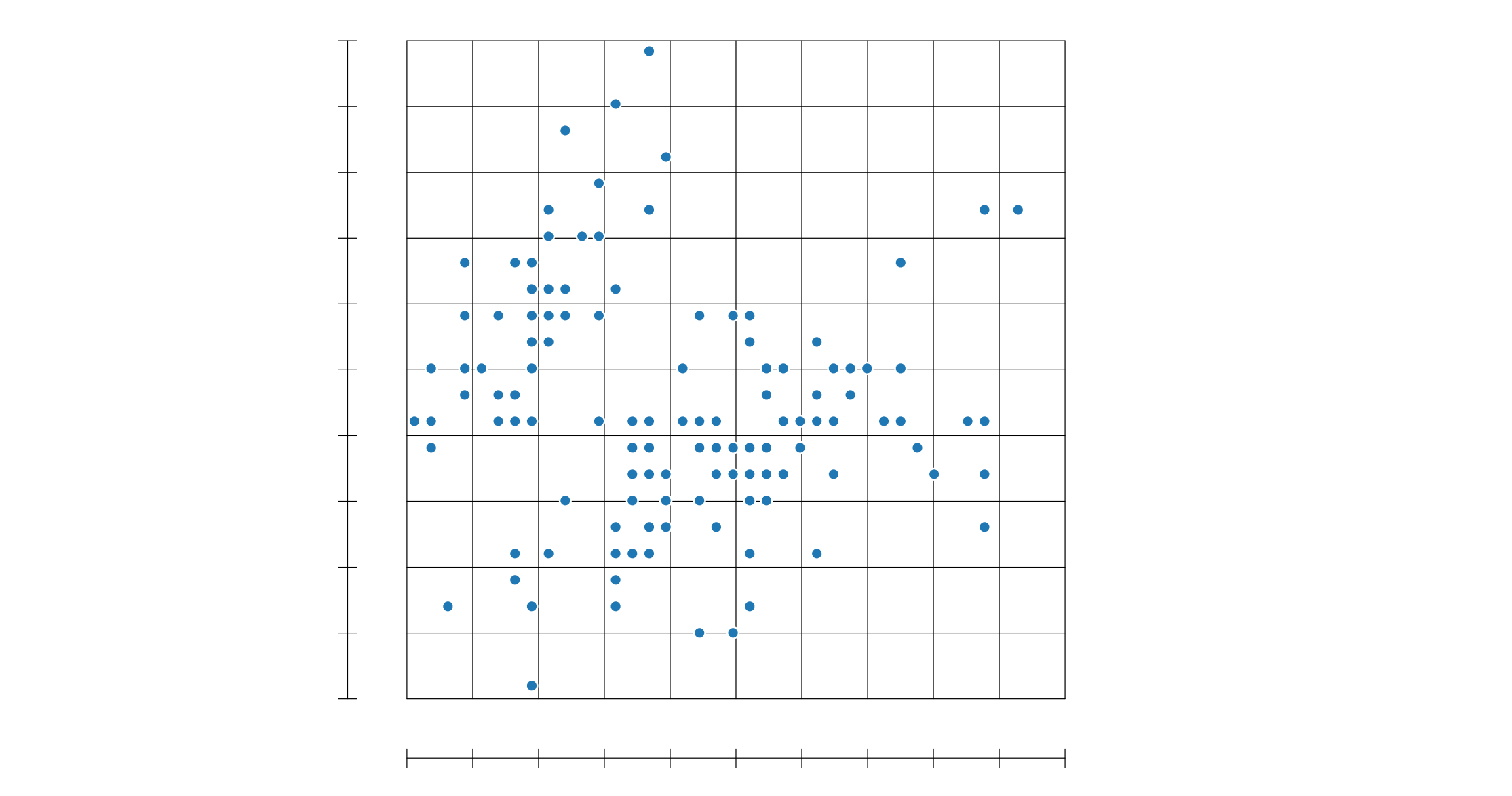
因此采用二维热力图：

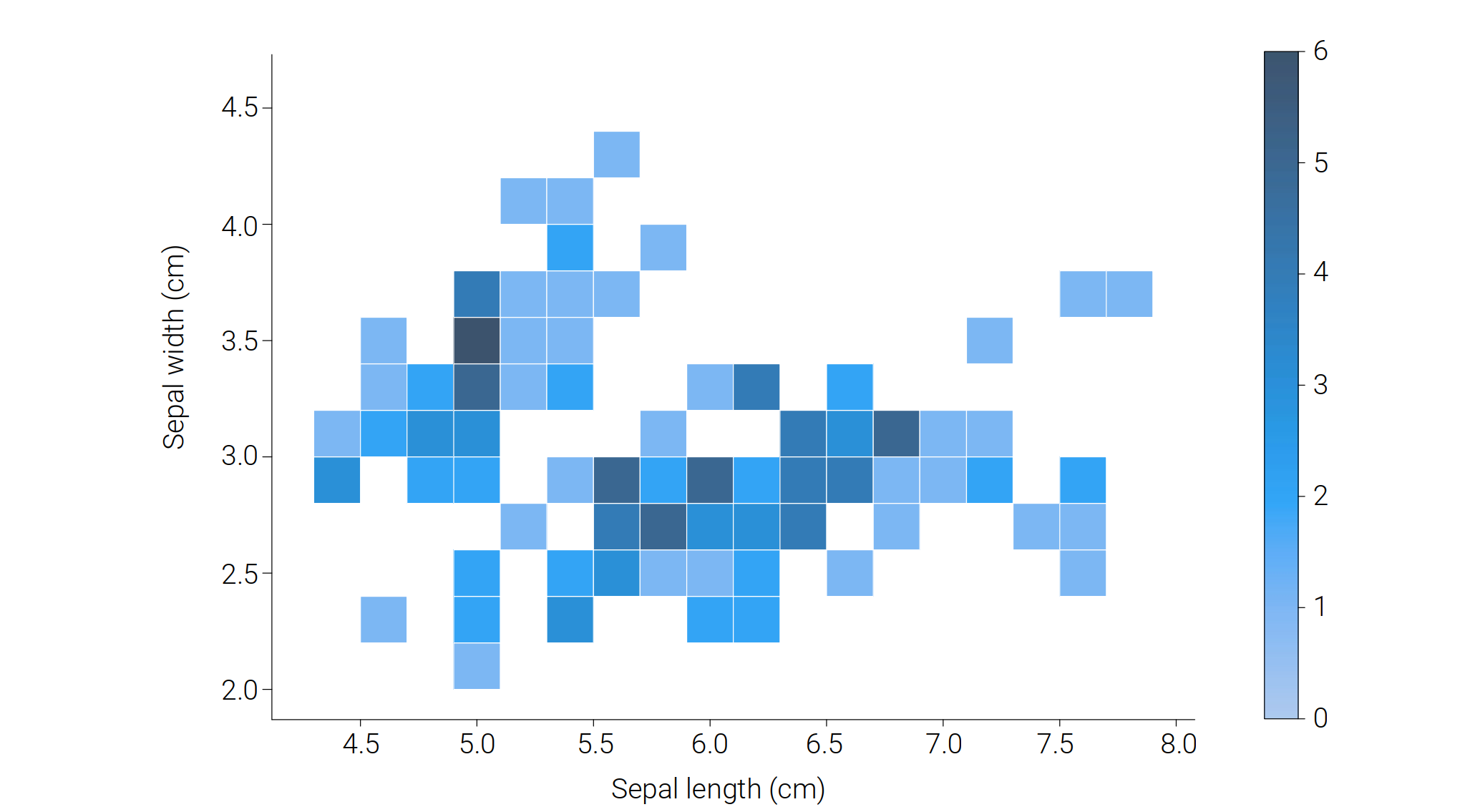
# 鸢尾花二元频率直方热图sns.displot(data=iris_sns, x="sepal_length", y="sepal_width", binwidth=(0.2, 0.2), cbar=True)

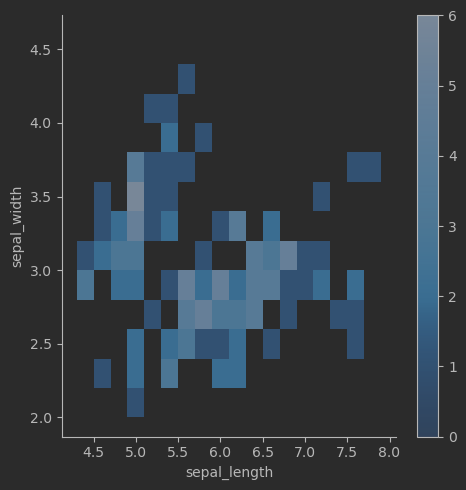
联合分布 KDE

使用高斯核函数可以估算联合分布，这样的联合分布可以用等高线图表示。

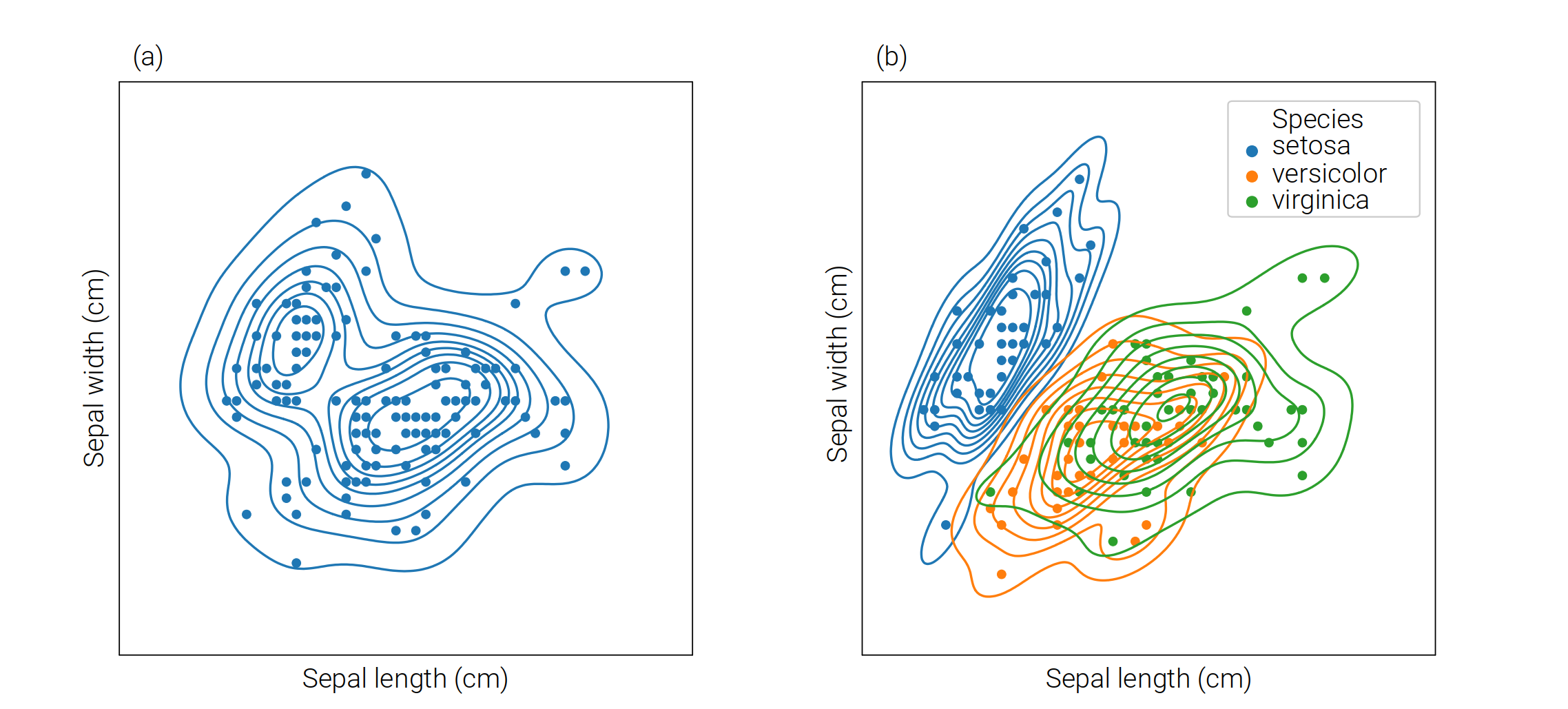
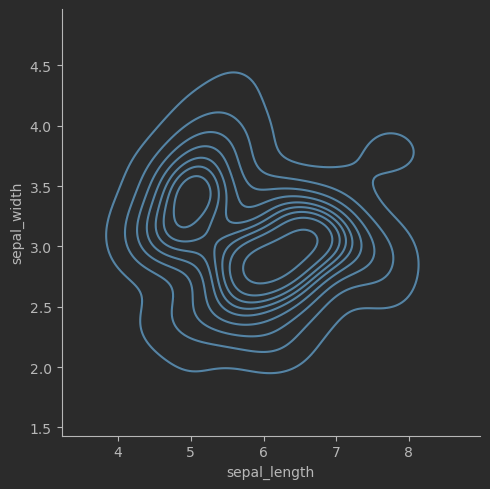
# 联合分布概率密度等高线
sns.displot(data=iris_sns, x="sepal_length", y="sepal_width", kind="kde")

效果：

# 联合分布概率密度等高线，考虑分布
sns.kdeplot(data=iris_sns, x="sepal_length", y="sepal_width", hue = 'species')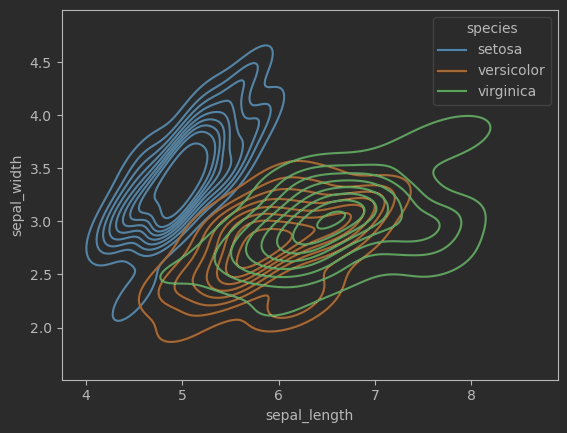

联合分布+边缘分布

看图即可懂：

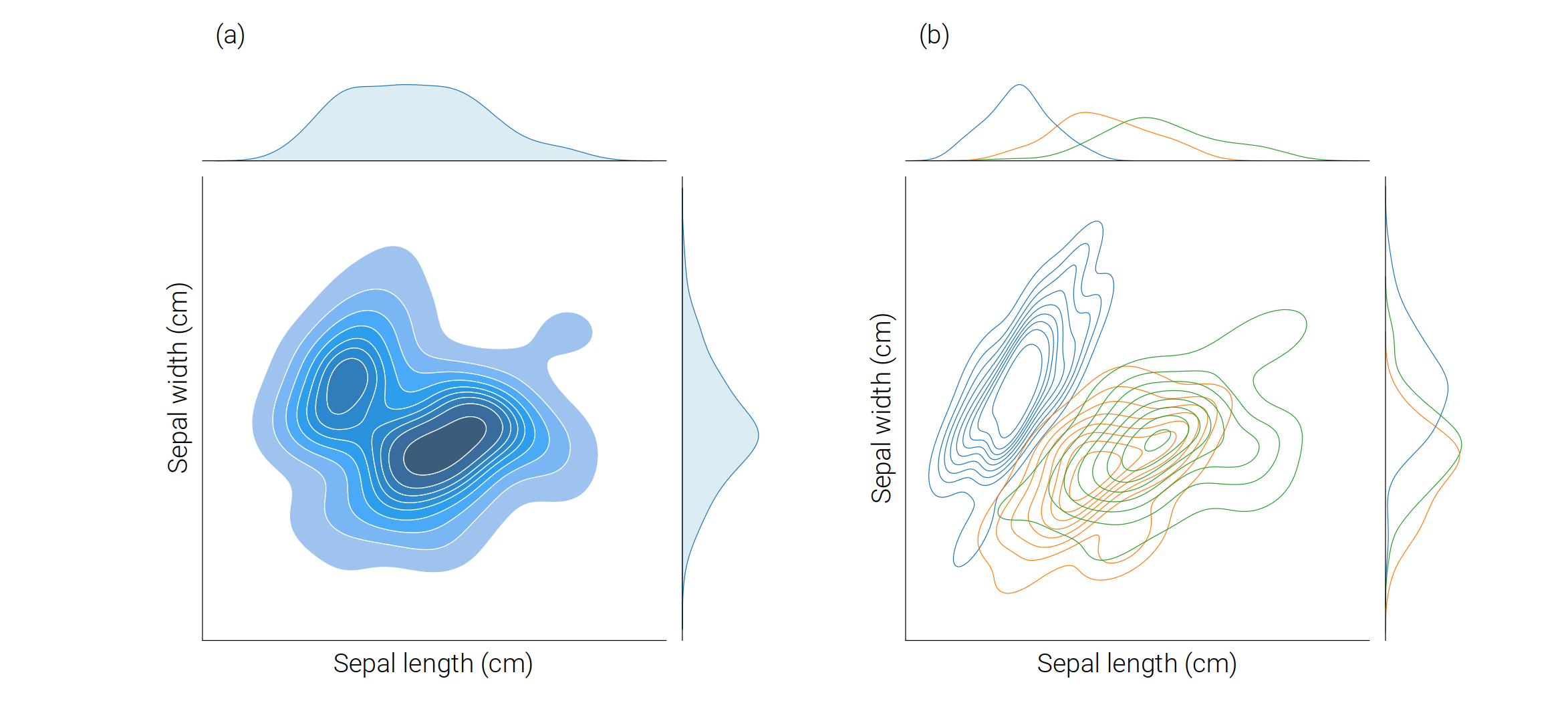
# 联合分布、边缘分布
sns.jointplot(data=iris_sns, x="sepal_length", y="sepal_width", kind = 'kde', fill = True)

这里仅放示范代码，其他代码查看附件。

线性回归

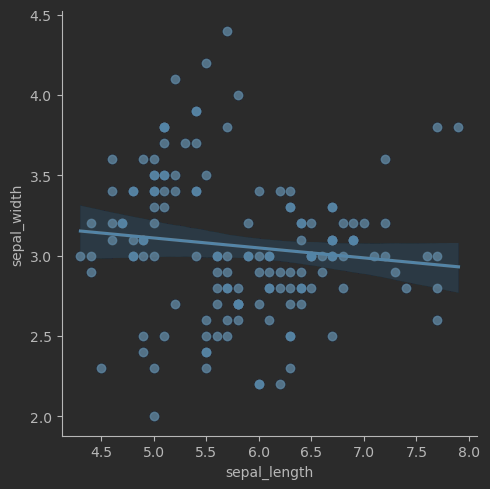
# 可视化线性回归关系
sns.lmplot(data=iris_sns, x="sepal_length", y="sepal_width")

效果：

多元特征数据

可以用一元可视化方案展现多元特诊
首先将宽格式转化为长格式。
原来的宽格式：

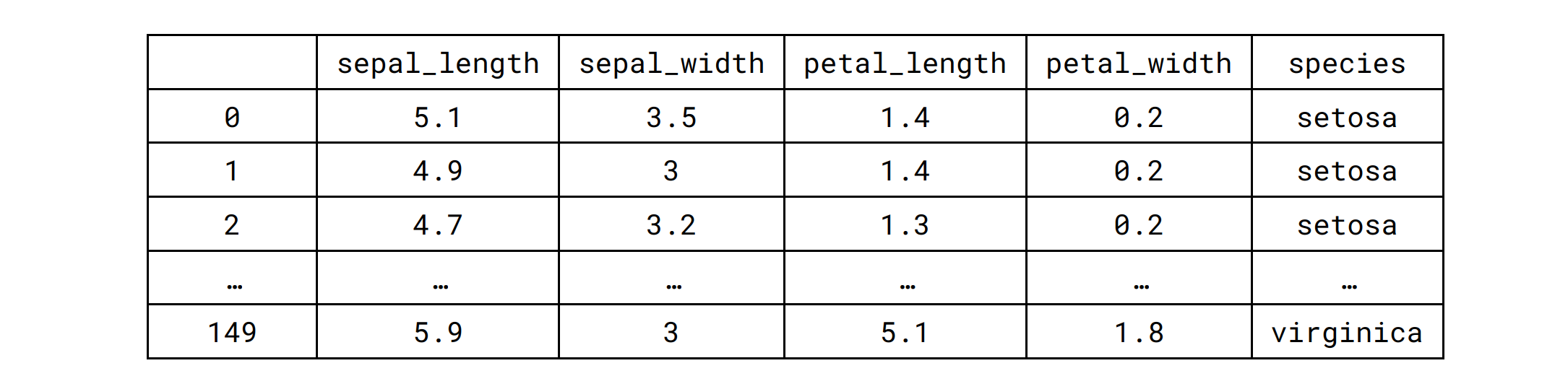
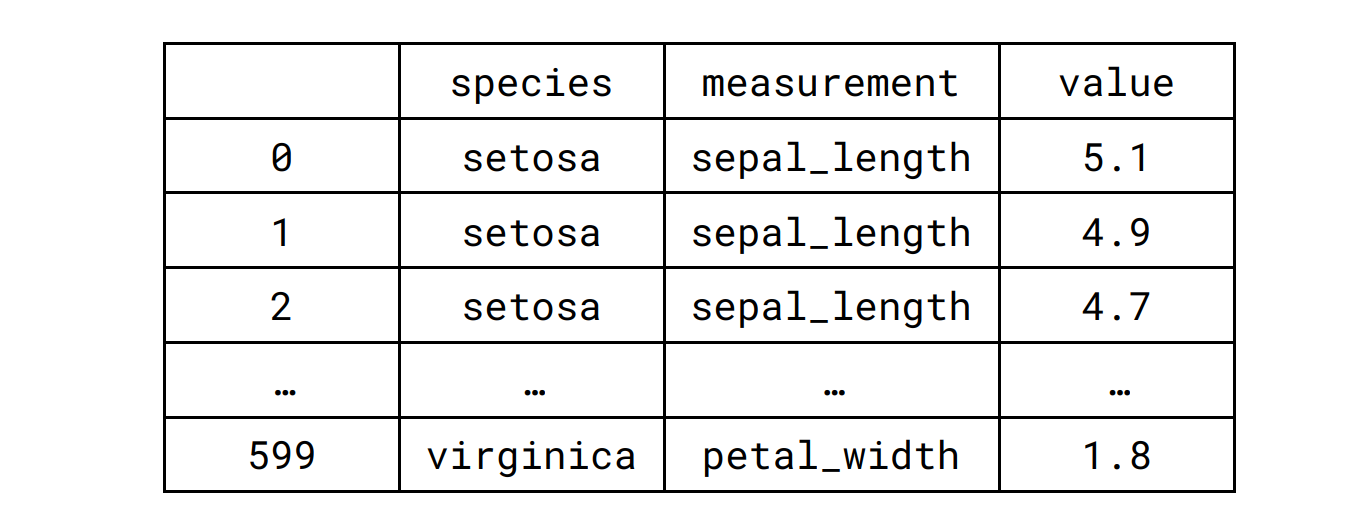
iris_melt = pd.melt(iris_sns, "species", var_name="measurement")
iris_melt

通过代码结果可以查看长数据：

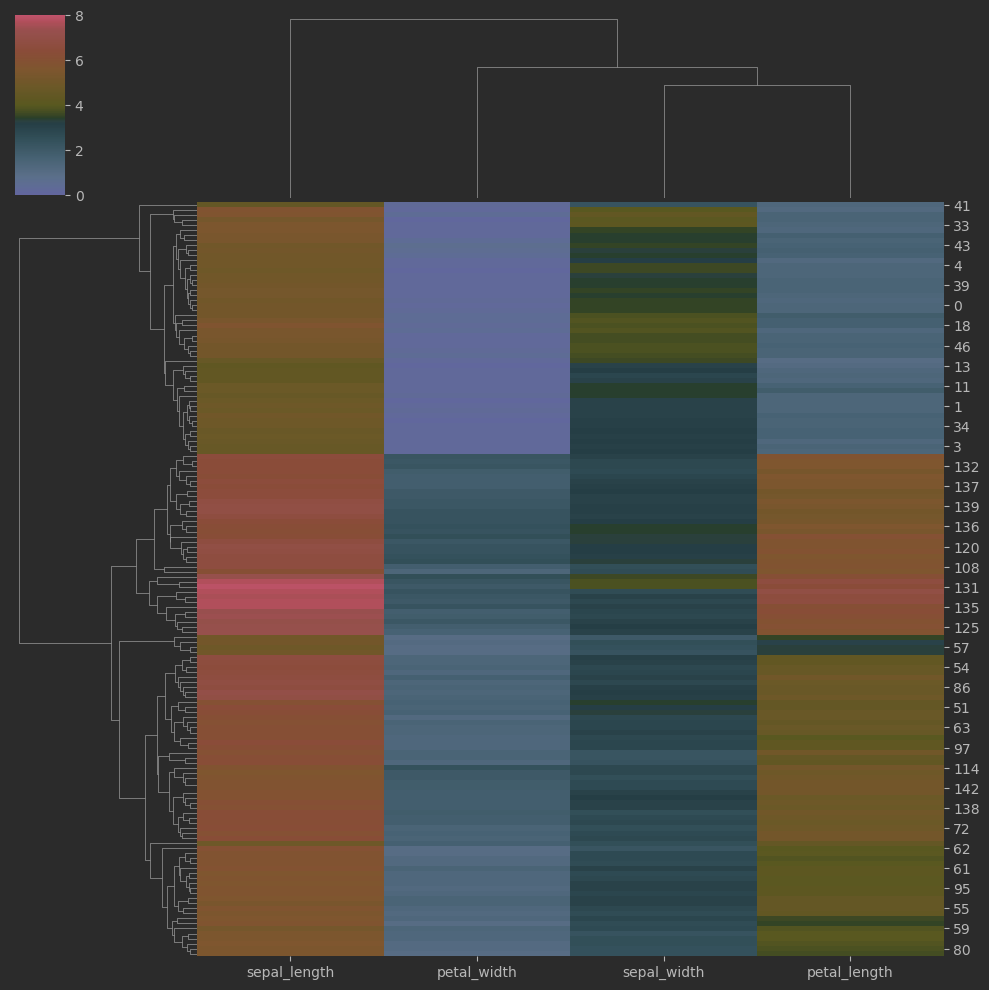
聚类热图

# 聚类热图
sns.clustermap(iris_sns.iloc[:,:-1], cmap = 'RdYlBu_r', vmin = 0, vmax = 8)

成对特征散点图

sns.pairplot(iris_sns)

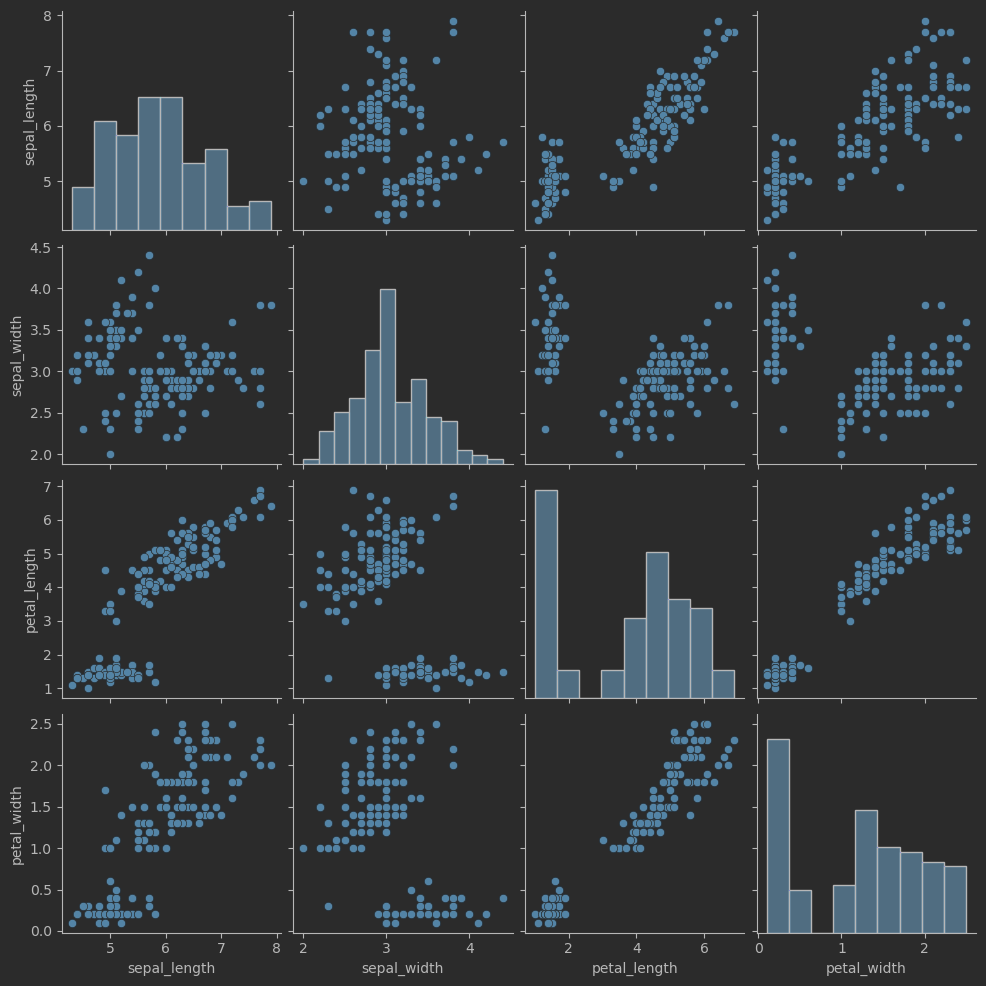
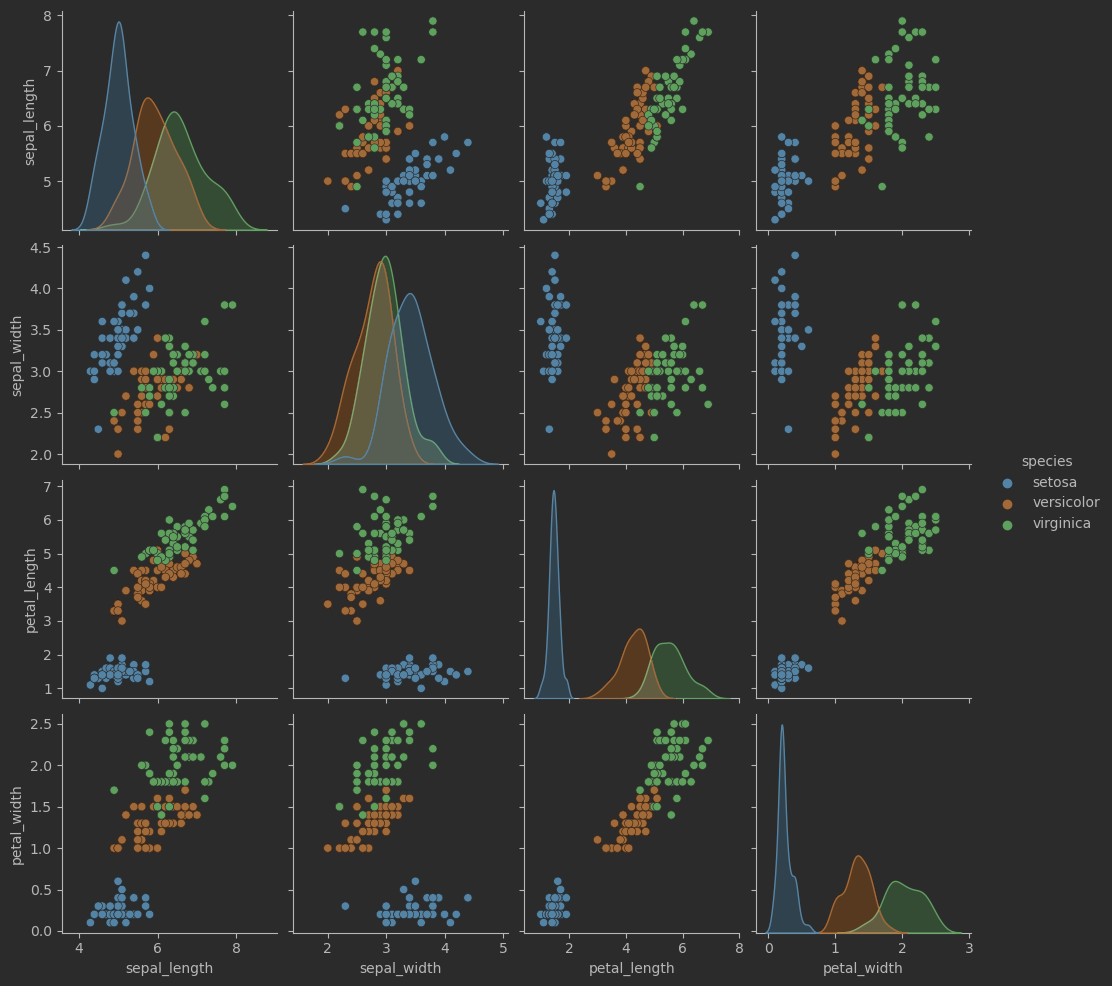
# 绘制成对特征散点图
sns.pairplot(iris_sns, hue = 'species')

效果：

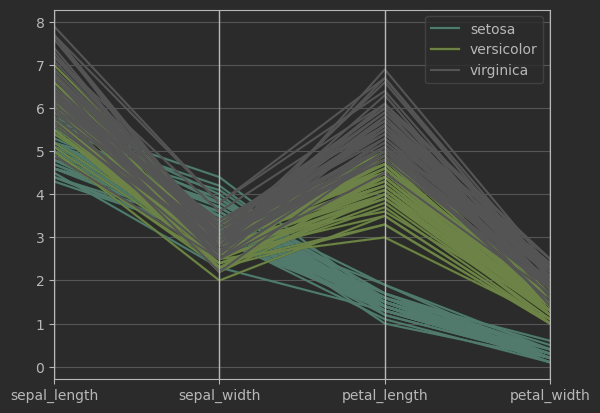
平行坐标图

from pandas.plotting import parallel_coordinates
# 可视化函数来自pandas
parallel_coordinates(iris_sns, 'species', colormap=plt.get_cmap("Set2"))
plt.show()