JavaScript递归
递归是 JavaScript 中一种重要的编程技术,指函数直接或间接调用自身的编程模式。它通过将复杂问题分解为相似的子问题来求解,特别适合处理树形结构、分治算法等场景。
一、递归的核心要素
1.终止条件(基线条件)
防止无限递归的关键
当满足条件时直接返回结果,不再调用自身
示例:阶乘中
n === 1时返回 1
2.递归调用
将问题分解为更小的同类子问题
示例:阶乘中
n * fact(n - 1)
// 阶乘递归实现
function factorial(n) {if (n === 1) return 1; // 终止条件return n * factorial(n - 1); // 递归调用
}
console.log(factorial(5)); // 120 (5*4*3*2*1)
二、经典应用场景
1.数学计算
// 斐波那契数列
function fibonacci(n) {if (n <= 1) return n;return fibonacci(n - 1) + fibonacci(n - 2);
}
console.log(fibonacci(6)); // 8 (0,1,1,2,3,5,8)
2.数据结构遍历
// 深度优先遍历树结构
function traverseTree(node) {console.log(node.value);node.children.forEach(child => traverseTree(child));
}
3.文件/目录处理
// 递归扫描目录(伪代码)
function scanDirectory(dir) {fs.readdir(dir, (err, files) => {files.forEach(file => {const path = `${dir}/${file}`;if (isDirectory(path)) scanDirectory(path); // 递归调用else processFile(path);});});
}
三、递归与循环对比
| 特性 | 递归 | 循环 |
|---|---|---|
| 实现方式 | 函数自我调用 | for/while 重复执行代码块 |
| 状态管理 | 通过参数传递状态 | 修改外部变量 |
| 终止条件 | 基线条件(base case) | 循环条件表达式 |
| 内存占用 | 栈空间累积(可能栈溢出) | 固定内存占用 |
| 代码可读性 | 复杂问题更简洁 | 简单问题更直观 |
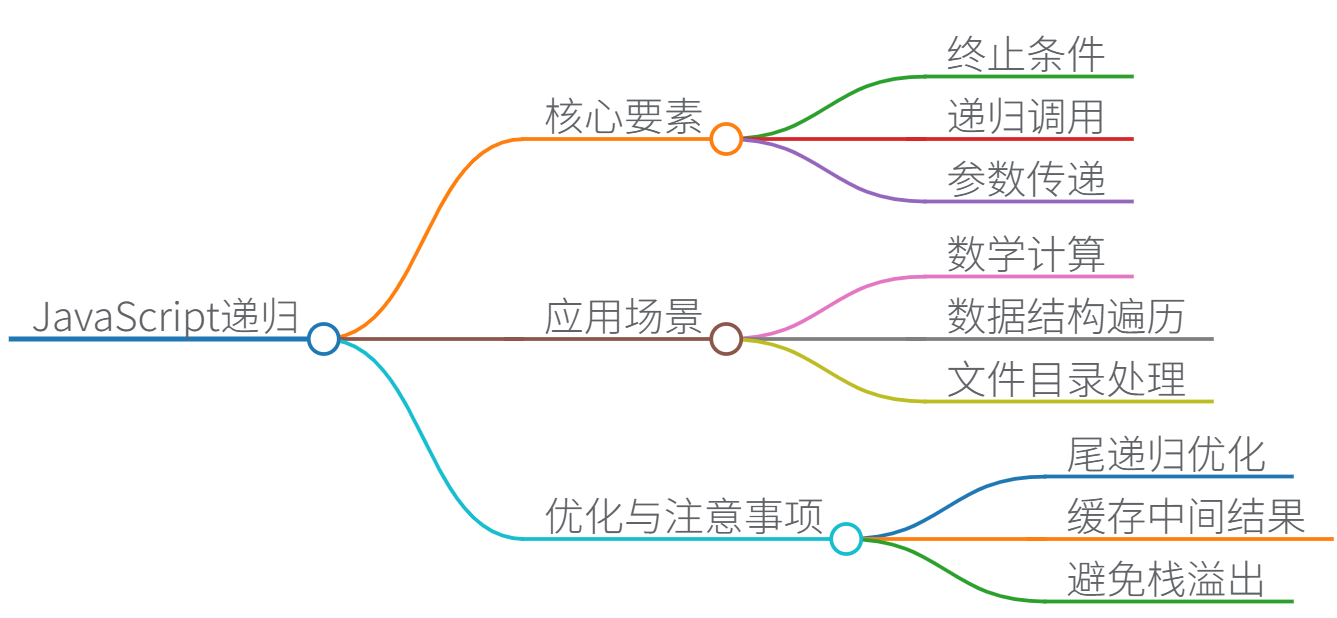
四、递归优化策略
1.尾递归优化
将递归调用放在函数最后一步,避免栈累积:
// 尾递归阶乘
function factorial(n, total = 1) {if (n === 1) return total;return factorial(n - 1, n * total); // 尾调用
}
2.缓存中间结果(Memoization)
避免重复计算:
// 带缓存的斐波那契
const memo = {};
function fibMemo(n) {if (n <= 1) return n;if (memo[n]) return memo[n]; // 读取缓存memo[n] = fibMemo(n - 1) + fibMemo(n - 2); // 存储缓存return memo[n];
}
3.循环替代
对于深度可能过大的场景:
// 循环实现阶乘
function factorialLoop(n) {let result = 1;for (let i = 2; i <= n; i++) {result *= i;}return result;
}
五、使用注意事项
栈溢出风险
JavaScript 引擎有调用栈深度限制(约 1-2 万层),深度递归需谨慎。性能考量
递归调用涉及上下文切换,性能通常低于循环。对于性能敏感场景应进行基准测试。明确终止条件
缺少终止条件会导致无限递归,浏览器可能抛出 “Maximum call stack size exceeded” 错误。
递归的核心价值在于用简洁的代码表达分治逻辑,但需权衡可读性与性能。对于树处理、回溯算法等场景,递归仍是首选方案。
