当前位置：首页 > news >正文

力扣（接雨水）——单调栈

news 2025/8/16 10:47:27

深度解析 LeetCode 42. 接雨水：单调栈的精妙应用

一、题目剖析

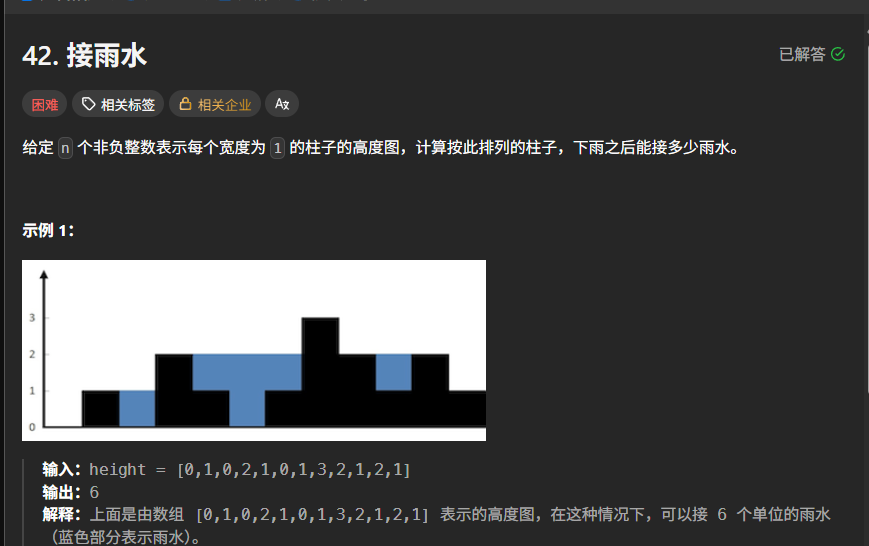
在这里插入图片描述

（一）问题描述

给定表示柱子高度的非负整数数组 height，计算下雨后这些柱子能承接的雨水总量。雨水承接的关键在于找到“凹槽”—— 左右两侧有更高的柱子，中间较低，从而形成储水空间。

（二）核心挑战

凹槽识别：需精准定位所有可能储水的凹槽，判断其左右边界（更高的柱子）和底部（较低的柱子）。
容量计算：每个凹槽的储水量由左右边界的较低高度、底部高度以及凹槽宽度决定，需高效遍历并计算。
时间复杂度优化：避免暴力枚举所有可能的凹槽（时间复杂度过高），需借助单调栈等数据结构，实现线性时间复杂度的解法。

二、算法思想：单调栈的高效应用

（一）单调栈的作用

使用单调递增栈（栈中元素对应的柱子高度单调递增），用于：

追踪凹槽边界：栈底到栈顶，柱子高度递增。当遇到更高的柱子时，可能形成凹槽，栈中低于当前高度的元素可作为凹槽的底部或中间部分。
计算储水容量：通过栈的弹出操作，确定凹槽的左右边界（栈顶弹出后的新栈顶为左边界，当前柱子为右边界）和底部（弹出的元素），进而计算该凹槽的储水量。

（二）栈的操作逻辑

入栈规则：遍历柱子时，若当前柱子高度小于栈顶元素对应的高度，入栈（保持栈的单调递增）；若当前高度大于等于栈顶高度，开始处理栈中的凹槽。
出栈与储水计算：当遇到更高柱子时，持续弹出栈顶元素，直到栈为空或栈顶元素更高。每次弹出时，计算该凹槽的储水量—— 以左右边界的较低高度、底部高度的差值为“有效高度”，乘以凹槽宽度（左右边界间距 - 1 ），累加到总雨水量。

三、代码实现与深度解析

//单调栈：单调递增
class Solution {public int trap(int[] height) {Stack<Integer> st = new Stack<>();int sumRain = 0;//初始化栈的第一个元素st.push(0);for (int i = 1; i < height.length; i++) {//如果当前高度小于栈顶高度，入栈，不形成水坑if (height[i] < height[st.peek()]) {st.push(i);} else {//出栈while (!st.empty() && height[i] >= height[st.peek()]) {int curr = st.pop(); // 凹槽底部下标if (st.empty()) {break; // 无左侧边界，无法储水}int perv = st.peek(); // 左侧更高柱下标int next = i; // 右侧更高柱下标// 计算凹槽宽度和高度sumRain += (next - perv - 1) * (Math.min(height[next], height[perv]) - height[curr]);}//将当前元素入栈st.push(i);}}return sumRain;}
}

（一）代码执行流程

初始化：创建单调递增栈 st，存储柱子下标；sumRain 初始化为 0，记录总储水量。将第一个柱子下标（0 ）入栈，初始化栈结构。
遍历柱子：从第二个柱子（i = 1 ）开始遍历 height 数组：
- 情况 1：当前柱子高度 height[i] < 栈顶下标对应的高度，直接入栈，维持栈的单调递增。
- 情况 2：当前柱子高度 >= 栈顶下标对应的高度，开始处理凹槽：
  - 循环弹出栈顶元素 curr（凹槽底部），直到栈空或栈顶元素更高。
  - 若栈空，说明无左边界，无法储水，跳出循环。
  - 确定凹槽的左边界（新栈顶 prev ）、右边界（i ），计算该凹槽的储水量（有效高度 × 宽度），累加到 sumRain 。
  - 当前柱子下标入栈，继续维持栈的单调递增。
返回结果：遍历结束后，sumRain 即为总接雨水量，返回该值。

（二）关键逻辑拆解

单调栈的维护：栈中存储柱子下标，保证下标对应的柱子高度单调递增。遇到更高柱子时，触发凹槽处理逻辑；否则维持栈的单调性。
凹槽处理：通过弹出栈顶元素，确定凹槽的底部、左右边界。利用左右边界的较低高度与底部高度的差值，计算有效储水高度；通过左右边界下标差，计算凹槽宽度。两者相乘得到该凹槽的储水量。
边界条件处理：栈空时，说明无左边界，无法储水，及时跳出循环，避免无效计算。