KNN算法:从电影分类到鸢尾花识别
在机器学习的众多算法中,K近邻算法(KNN)以其简单易懂、贴近生活的特点,成为入门者的理想学习对象。
一、从电影分类说起:KNN的生活化场景
我们都知道,电影可以大致分为爱情片、动作片等类型,那这些类型是如何区分的呢?答案是通过电影中“打斗镜头次数”和“接吻镜头次数”这两个特征来划分。

表格中列出了6部已知类型的电影数据:
3部爱情片:《California Man》(3次打斗,104次接吻)、《He's Not Really into Dudes》(2次打斗,100次接吻)、《Beautiful Woman》(1次打斗,81次接吻),不难发现爱情片的共同特点是接吻镜头多、打斗镜头少。
3部动作片:《Kevin Longblade》(101次打斗,5次接吻)、《Robo Slayer 3000》(99次打斗,2次接吻)、《Amped II》(98次打斗,2次接吻),动作片则是打斗镜头多、接吻镜头少。
那么“?”这个未知电影(这里先留个悬念,它的类型未知,打斗镜头18次,接吻镜头90次)
正是基于这些已知电影的特征和类型,我们可以思考:如何判断未知电影的类型呢?这就引出了我们今天的主角——KNN算法。
二、KNN算法:“物以类聚”的简单智慧
KNN算法,全称K近邻算法(k-Nearest Neighbor),它的核心思想非常朴素,就像我们常说的“物以类聚,人以群分”。每个样本都可以用它最接近的K个邻近样本的特征来代表,通过这K个邻近样本的类别,就能推断出未知样本的类别。
1. 算法步骤拆解
KNN算法的工作流程可以总结为以下5个步骤:
1. 计算已知类别数据集中所有点与当前未知点之间的距离;
2. 按照距离从小到大的次序进行排序;
3. 选取与当前点距离最小的K个点;
4. 确定这K个点所在类别的出现频率;
5. 返回这K个点中出现频率最高的类别,作为当前未知点的预测分类。
2. K值的关键作用
K值是KNN算法中一个非常重要的超参数,它的取值会直接影响分类结果。通过图示直观地展示了这一点:
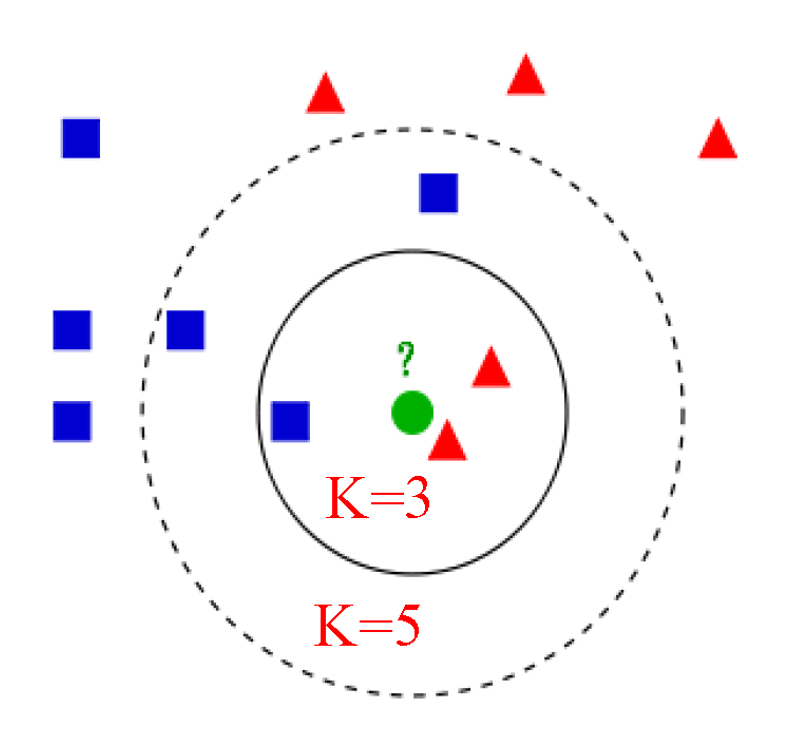
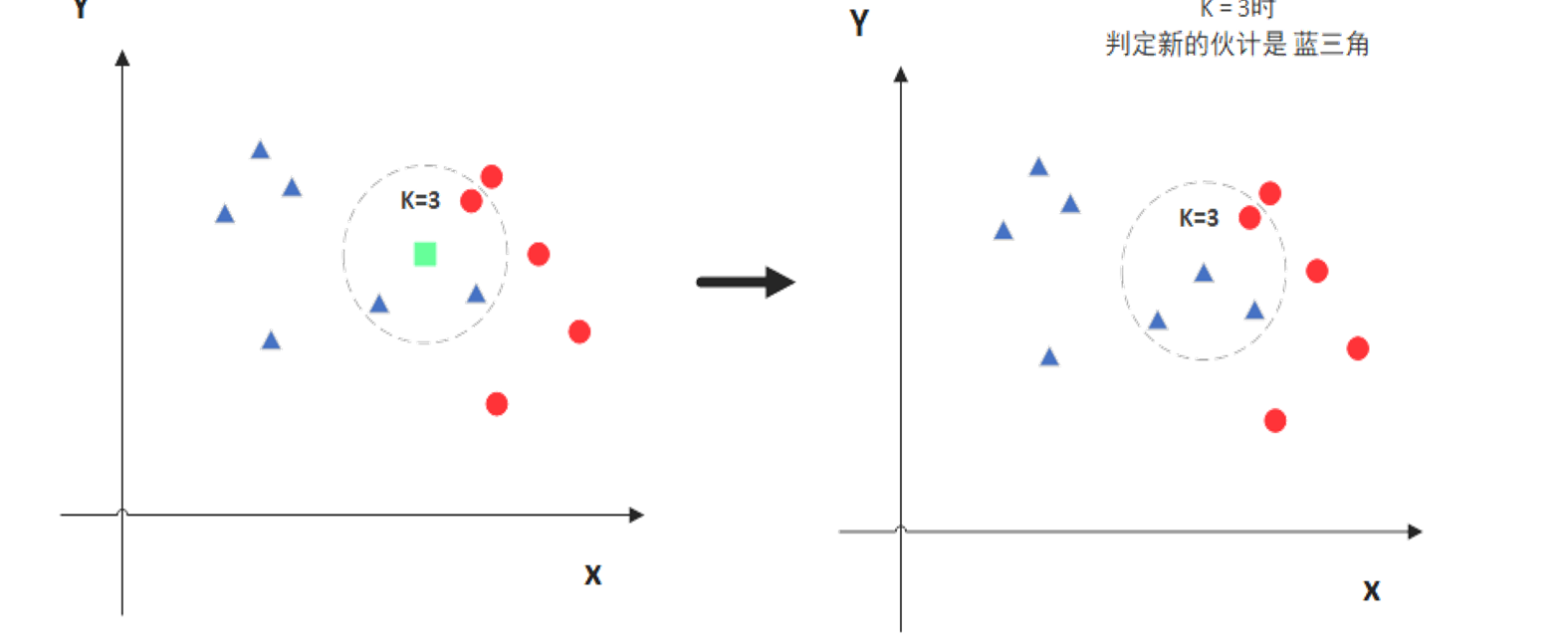
当K=3时,新样本被判定为“蓝三角”对应的类别;
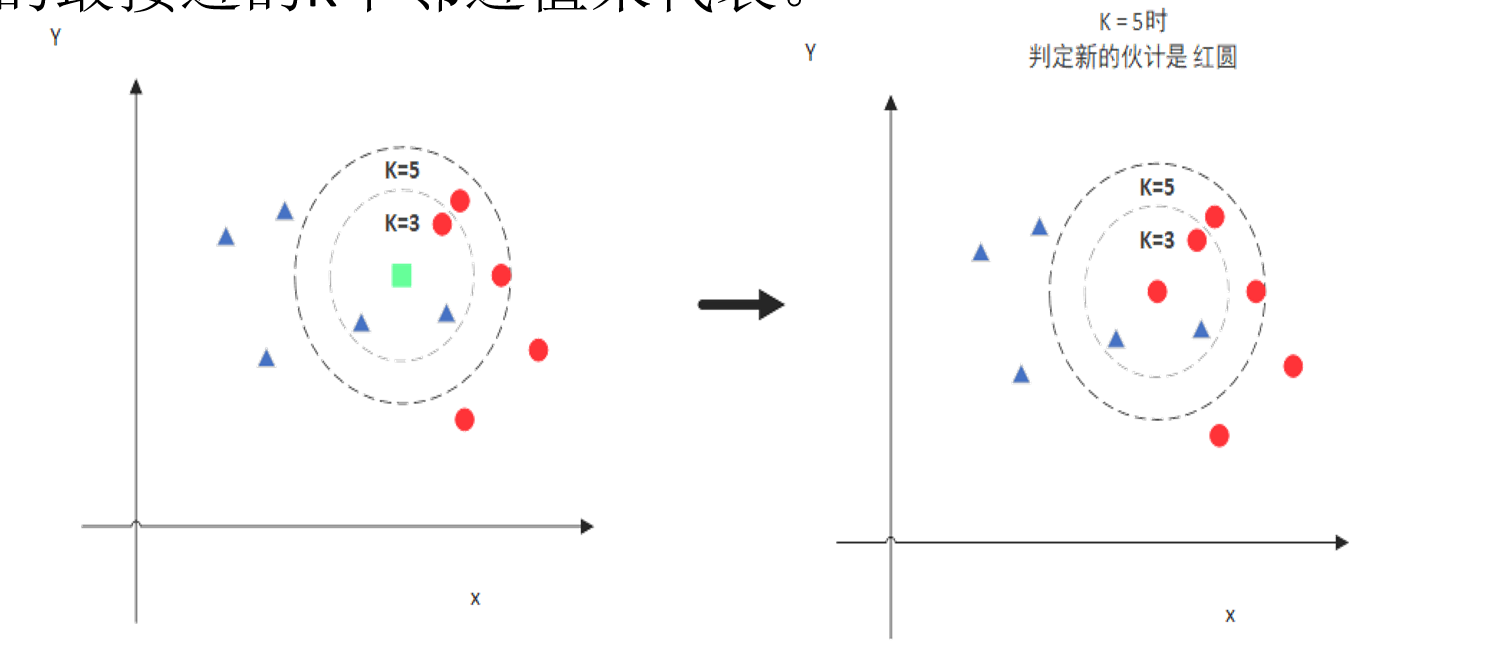
当K=5时,新样本则被判定为“红圆”对应的类别。
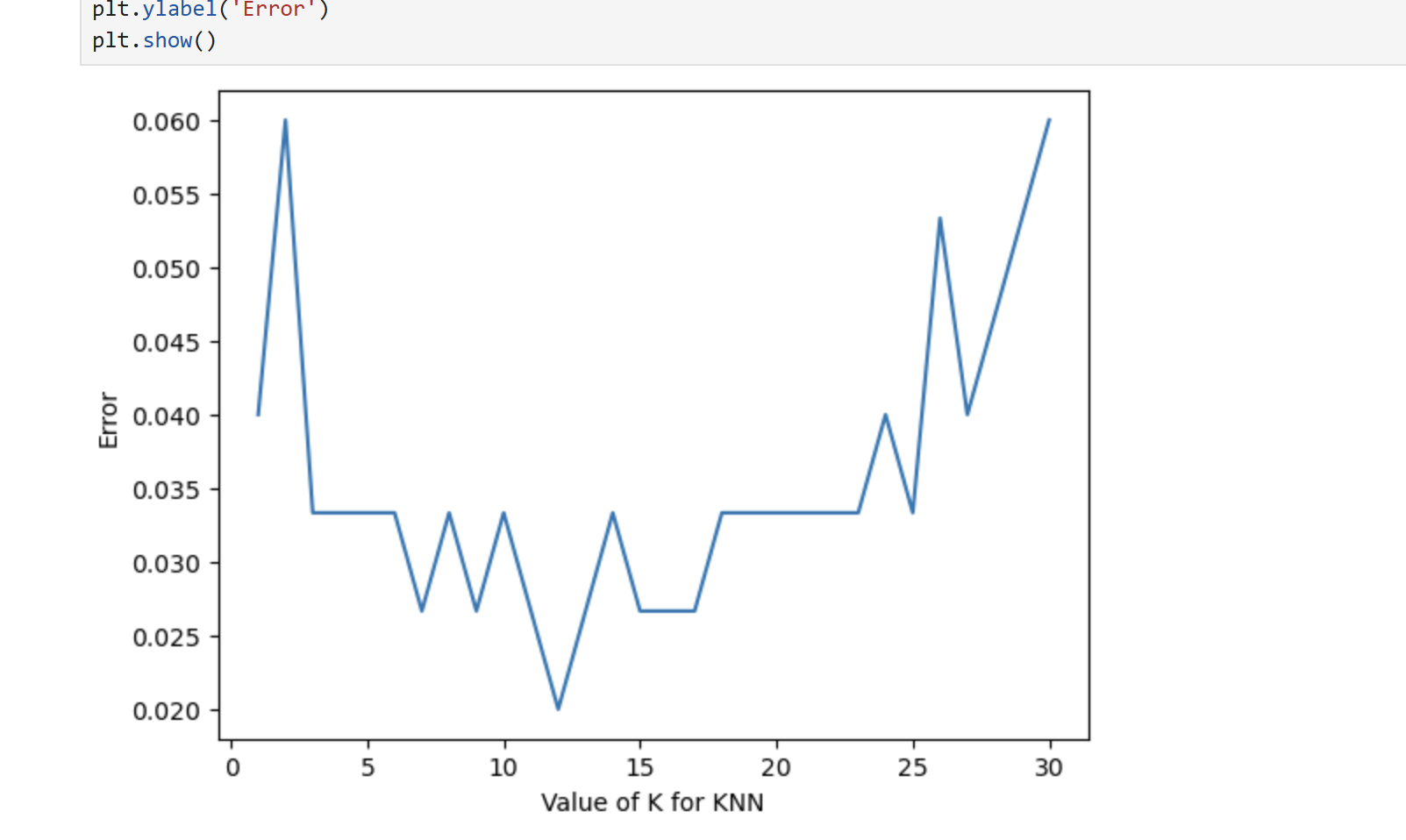
一般来说,K值不宜过大,通常不超过20。K值太小,模型容易受到噪声的影响,出现过拟合;K值太大,又可能模糊类别边界,导致欠拟合。在实际应用中,需要通过多次实验来选择最合适的K值。
三、距离度量:衡量“相似性”的标尺
在KNN算法中,如何衡量两个样本之间的“接近程度”呢?这就需要用到距离度量方法。这里运用到两种常用的距离度量方式:
1. 欧式距离
欧式距离也称欧几里得距离,是最常见的距离度量方式,它衡量的是多维空间中两个点之间的绝对距离。
在二维空间中,两点(x₁,y₁)和(x₂,y₂)之间的欧式距离公式为: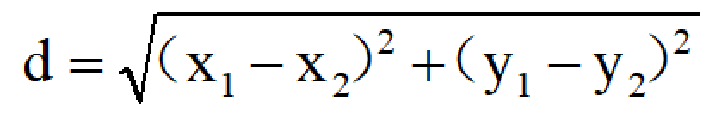
在三维空间中,公式则扩展为: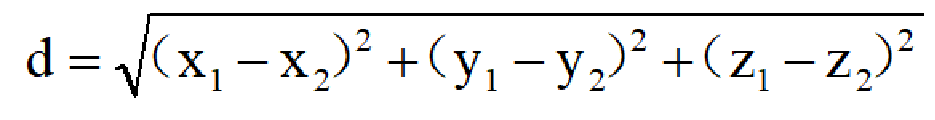
推广到n维空间,欧式距离公式为:(i从1到n)
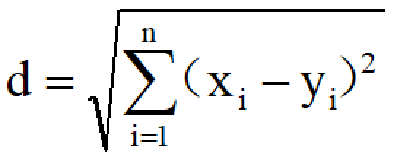
2. 曼哈顿距离
曼哈顿距离是由十九世纪的赫尔曼·闵可夫斯基提出的,它指的是两个点在标准坐标系上的绝对轴距总和,就像出租车在城市中行驶的距离一样,只能沿着直角方向移动。
在平面上,坐标(x₁,y₁)的点与坐标(x₂,y₂)的点之间的曼哈顿距离公式为:
d(i,j)=|X1-X2|+|Y1-Y2|
四、实战演练:KNN的应用案例
1. 鸢尾花分类
鸢尾花数据集是机器学习中的经典数据集,包含了3个品种的鸢尾花:Iris Versicolor、Iris Setosa、Iris Virginica,每个品种有50个样本,每个样本包含4个特征:花萼长度(sepal length)、花萼宽度(sepal width)、花瓣长度(petal length)、花瓣宽度(petal width)(单位:cm)。
基于KNN算法,实现鸢尾花分类的步骤如下:
加载数据集:
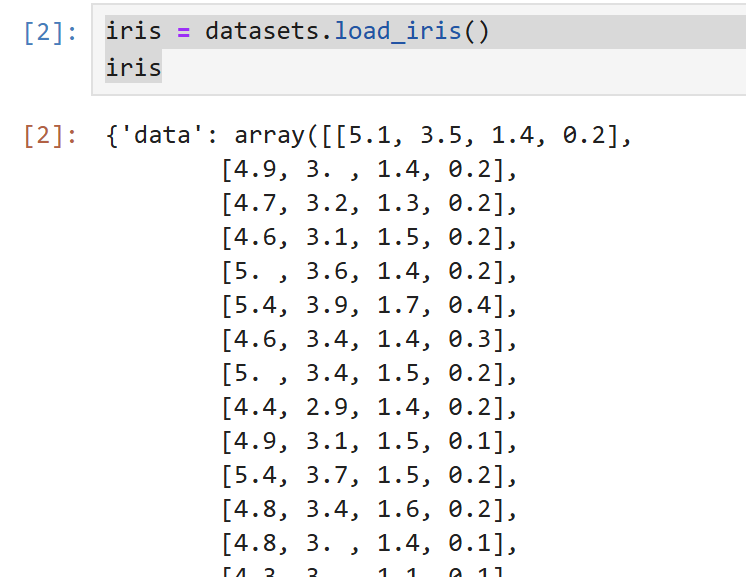
划分训练集和测试集:将数据分为 70% 训练集(用于训练模型)和 30% 测试集(用于评估模型),避免模型 “记住” 训练数据而失去泛化能力。
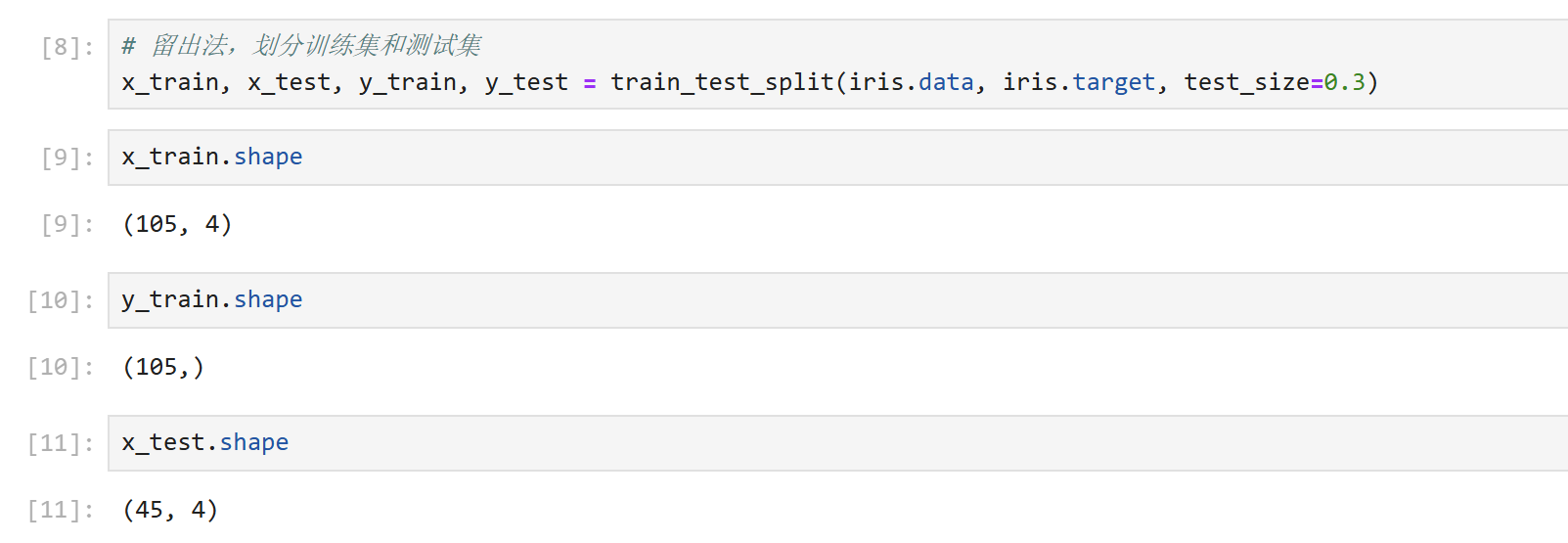
训练模型:创建KNN实例,设置K值为5,距离度量采用欧式距离,然后进行训练:

评估模型:计算训练集和测试集的得分,评估模型的性能:
预测结果:对测试集的样本进行预测:`y_pred = knn.predict(x_test)`
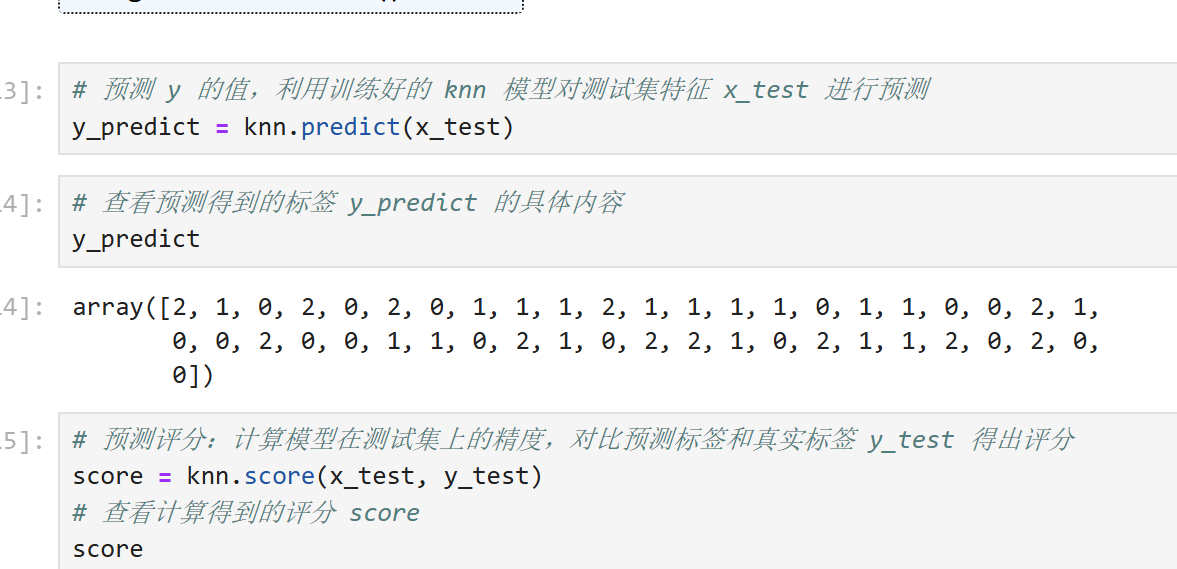
最后得到结果:
2. 未知电影类型判断
回到开篇的电影分类问题,我们可以用KNN算法来判断未知电影的类型。通过计算未知电影与已知电影的距离,选取距离最近的K个电影,根据这K个电影的类型,就能推断出未知电影的类型。
计算未知电影与所有已知电影的距离(以欧式距离为例):
| 电影名称 | 距离计算 | 距离值 | 类型 |
|---|---|---|---|
| Beautiful Woman(爱情片) | (18−1)2+(90−81)2=289+81=370≈19.2 | 19.2 | 爱情片 |
| California Man(爱情片) | (18−3)2+(90−104)2≈20.5 | 20.5 | 爱情片 |
| He's Not Really into Dudes(爱情片) | (18−2)2+(90−100)2=256+100≈18.8 | 18.8 | 爱情片 |
| Kevin Longblade(动作片) | (18−101)2+(90−5)2≈6889+7225≈118.8 | 118.8 | 动作片 |
| Robo Slayer 3000(动作片) | 距离更大(约 117.7) | - | 动作片 |
筛选最近的 3 个邻居:均为爱情片(距离 18.8、19.2、20.5),因此预测未知电影为爱情片。
总结
KNN算法的优势在于简单直观,不需要复杂的模型训练过程,易于理解和实现。但它也有不足之处,比如计算成本较高,因为需要计算未知样本与所有已知样本的距离。通过学习,我们不仅掌握了KNN算法的基本原理和应用方法,更重要的是体会到了机器学习算法与实际生活的紧密联系。
