树形DP详解

今天呢我将给大家讲一个叫做树形DP的东西啊，这是个什么呢，好难猜呀

声明：该文章有可能会重制

本质

树形DP的本质就是树上面的DP，那么树上面该怎么DP呢，大家回顾一下DP的本质，通过前面的状态推到后面的状态，那么树形DP就是根据叶子推断根节点的值的一种DP（问题一般都不是什么单纯的合并点的问题，而是一些复杂的，看着像DP但是数据结构是树的题目），总而言之，树形DP如名字所显示，在树上面进行DP

题目

光讲大家可能听不懂，来一道题大家就明白了。

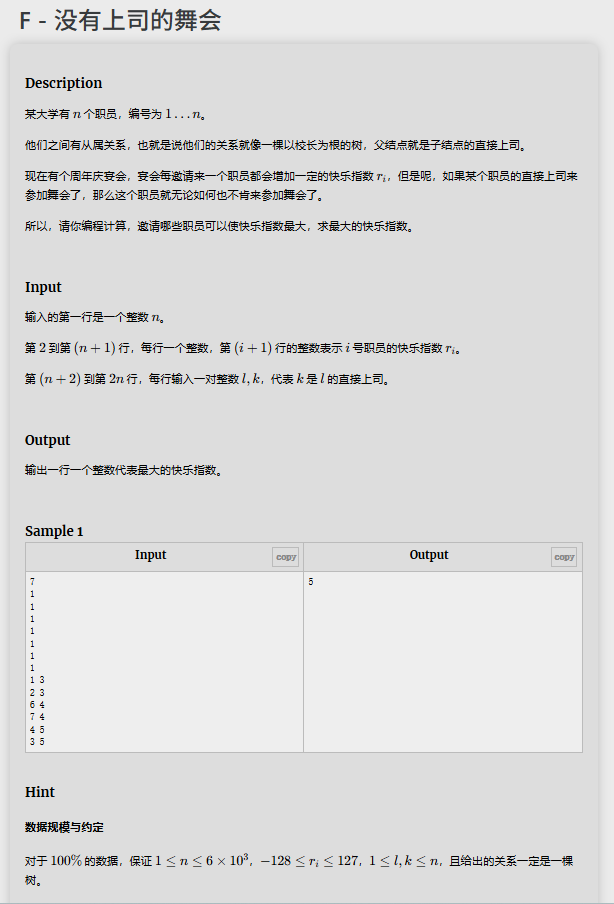
那么这道题求的是最大最小，看着就是DP，又是树，那么答案就出来啦，他是树形DP！！！

那该如何解决呢？首先设dp[节点数][2]，dp[i][0]表示第i个点不参加会有什么情况（下面的点可以参加也可以不参加，取最大值），dp[i][1]表示参加又是什么情况（下面的点只好不参加，取他们0的情况），然后取根节点的0和1的最大值就可以了。

#include<bits/stdc++.h>
#include<vector>
using namespace std;
int n,a[6010],root,dp[6010][2]; 
vector<int> tree[6010];
bool b[6010];
void dfs(int m){dp[m][1]=a[m];for(int v:tree[m]){dfs(v);dp[m][0]+=max(dp[v][0],dp[v][1]);dp[m][1]+=dp[v][0];}
}
int main(){cin>>n;for(int i=1;i<=n;i++){cin>>a[i];}for(int i=1;i<=n-1;i++){int l,k;cin>>l>>k;tree[k].push_back(l);b[l]=1;}for(int i=1;i<=n;i++){if(!b[i]){root=i;break;}}dfs(root);cout<<max(dp[root][0],dp[root][1]);
}

解释完成！