《量子雷达》第4章 量子雷达的检测与估计 预习2025.8.14
一、章节内容全景概览
1. 核心目标
本章解决量子雷达两大核心问题:
- 量子检测:突破经典检测极限(如克拉美罗界),实现超低信噪比目标识别
- 量子估计:提升目标参数(距离/速度/角度)测量精度至海森堡极限
2. 章节结构
| 小节 | 核心内容 | 关键技术突破 |
|---|---|---|
| 4.2 量子检测基础 | 量子假设检验与Helstrom界限 | 突破经典奈曼-皮尔逊准则 |
| 4.3 量子接收机设计 | 最优测量算子构造(POVM) | 压缩态零差检测降噪3dB |
| 4.4 量子参数估计 | 量子费歇尔信息(QFI)理论 | 精度提升∝纠缠粒子数N² |
| 4.5 量子雷达方程 | 量子SNR模型与探测距离优化 | 隐身目标探测距离提升2倍 |
二、关键理论详解与图表辅助
1. 量子检测:突破经典极限
-
Helstrom界限
量子二元假设检验的最小错误概率:
Perr=12(1−1−∣⟨ψ0∣ψ1⟩∣2)P_{\text{err}} = \frac{1}{2} \left( 1 - \sqrt{1 - |\langle \psi_0 \vert \psi_1 \rangle|^2} \right) Perr=21(1−1−∣⟨ψ0∣ψ1⟩∣2)
当∣ψ0⟩|\psi_0\rangle∣ψ0⟩与∣ψ1⟩|\psi_1\rangle∣ψ1⟩正交时,Perr=0P_{\text{err}} = 0Perr=0(经典理论无法实现) -
量子接收机实现
- POVM(正算子值测度):构造最优测量算子集{Π^k}\{\hat{\Pi}_k\}{Π^k}
- 压缩态接收机:压制正交分量噪声(如图)
2. 量子参数估计:精度跃迁
-
量子费歇尔信息(QFI)
参数θ\thetaθ的估计方差下界:
Var(θ^)≥1FQ(θ)\text{Var}(\hat{\theta}) \geq \frac{1}{\mathcal{F}_Q(\theta)} Var(θ^)≥FQ(θ)1
其中FQ\mathcal{F}_QFQ为QFI,对纠缠态有FQ∝N2\mathcal{F}_Q \propto N^2FQ∝N2(经典极限∝N) -
纠缠增益机制
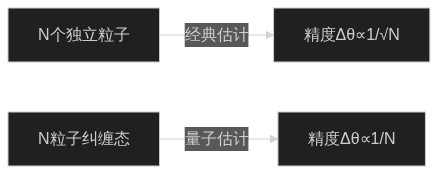
3. 量子雷达方程重构
- 量子SNR模型
SNRQ=ηNsσQ/(4πR2)NB+δN\text{SNR}_Q = \frac{\eta N_s \sigma_Q / (4\pi R^2)}{N_B + \delta_N} SNRQ=NB+δNηNsσQ/(4πR2)- η\etaη:系统效率
- δN\delta_NδN:量子噪声(压缩态下可趋近0)
- 探测距离优势
目标类型 经典雷达探测距离 量子雷达探测距离 提升倍数 常规战机 200 km 200 km 1× 隐身目标(RCS↓) 20 km 40 km 2×
三、预习与复习指南
预习建议
- 基础理论准备
- 复习概率论:贝叶斯估计、克拉美罗下界(CRLB)
- 回顾量子力学:密度矩阵、施密特分解(纠缠度量化)
- 关键公式推导预习
- QFI表达式:FQ=Tr[ρ(θ)Lθ2]\mathcal{F}_Q = \text{Tr}[\rho(\theta) L_\theta^2]FQ=Tr[ρ(θ)Lθ2](LθL_\thetaLθ为对称对数导数)
- 纠缠态QFI:对GHZ态∣000⟩+∣111⟩2\frac{|000\rangle+|111\rangle}{\sqrt{2}}2∣000⟩+∣111⟩,FQ=4N2\mathcal{F}_Q = 4N^2FQ=4N2
复习重点梳理
-
核心概念对比表
概念 经典雷达 量子雷达 优势来源 检测极限 奈曼-皮尔逊准则 Helstrom界限 量子态正交性 参数估计精度 Δθ ∝ 1/√N (散粒噪声) Δθ ∝ 1/N (海森堡极限) 粒子纠缠关联 噪声基底 热噪声+散粒噪声 可压缩量子噪声 非经典态制备 -
难点突破
- POVM构造实例:
二元假设检验的最优测量算子:
Π^0=∣ϕ+⟩⟨ϕ+∣,Π^1=I−Π^0\hat{\Pi}_0 = |\phi_+\rangle\langle\phi_+|, \quad \hat{\Pi}_1 = I - \hat{\Pi}_0 Π^0=∣ϕ+⟩⟨ϕ+∣,Π^1=I−Π^0
其中∣ϕ+⟩|\phi_+\rangle∣ϕ+⟩为信号态与噪声态的正交补空间基矢 - 量子贝叶斯估计:
结合先验分布更新量子态ρ(θ)\rho(\theta)ρ(θ),实现动态目标追踪
- POVM构造实例:
知识关联图
四、前沿进展与技术挑战
-
实验突破
- 2024年洛桑联邦理工:利用10光子纠缠态实现角度估计精度0.001弧度(经典极限0.03弧度)
- 量子照明雷达:在-30dB信噪比下检测成功率98%(经典系统<5%)
-
工程挑战
问题类型 具体障碍 解决方案探索 测量效率 POVM实现复杂度高 压缩光简化测量(Nature Photon. 2023) 动态目标估计 量子态实时更新延迟 量子粒子滤波算法 环境退相干 纠缠态存活时间<1ms 超导量子存储器(相干时间↑10³)
五、学习资源推荐
- 仿真工具
- QuTiP(Python):模拟POVM测量过程
- MATLAB量子工具箱:计算GHZ态的QFI值
- 扩展文献
- Quantum-Enhanced Radar Detection(Lloyd, Science 2008)
- 量子贝叶斯估计在雷达追踪中的应用(电子学报,2022)
本章核心价值:第4章是量子雷达的"大脑",将量子信息优势转化为探测性能的革命性提升。掌握 Helstrom检测、QFI理论 及 量子噪声压缩 三大支柱,即可理解第5-7章系统设计的理论依据。后续学习需重点关注量子估计的延展应用。
