STL——容器——容器适配器
容器适配器
| 适配器 | 默认底层容器 | 提供的抽象接口 | 头文件 |
| stack | deque | 栈(后进先出 LIFO) | <stack> |
| queue | deque | 队列(先进先出 FIFO) | <queue> |
| priority——queue | vector | 优先级队列(堆) | <queue> |
容器适配器(Container Adapter)不是一种新的数据结构,而是一种 “包装/转换”机制:
它在已有的顺序容器(vector / deque / list)之上 加一层接口限制或行为调整,从而得到另一种抽象数据结构。
注意:
容器适配器 没有 迭代器:因为本来就是要对行为 作 限制 才提供了可以使用的接口,用以实现抽象类型(LIFO、FIFO 等 其他 数据限制规则)。
迭代器的意义:迭代器是连接算法与容器的通用“指针-概念” —— 它把“如何遍历”封装起来,让 同一段算法代码 能在 任意容器 上工作,而无需关心容器内部结构。
stack

手撕环节 & 思路
STL手撕通用思路:
1. 抽象 → 2. 骨架 → 3. 填肉 → 4. 异常 → 5. 拷贝 → 6. 迭代器/比较
抽象
限制:后进先出 Last In First Out
实现:容器适配器、底层可以是 vector、list、deque 等序列容器
关键接口:push、pop、top、size、empty
骨架
先把模板头、成员变量、空壳函数写出来
template<class T, class Container = std::deque<T>>
class myStack {
public:void push(const T& val) {}void pop(){}T& top(){}size_t size(){}bool empty(){}private:Container _c;
};填肉
逐个 正向实现 成员函数,之后再考虑 异常安全
template<class T, class Container = std::deque<T>>
class myStack {
public:void push(const T& val) {_c.push_back(val);}void pop(){_c.pop_back();}T& top(){return _c.back();}size_t size(){return _c.size();}bool empty(){return _c.empty();}private:Container _c;
};容器适配器的成员函数实现,几乎完全依赖 底层容器
异常
容器适配器的异常 一般 无需额外处理,交给底层容器
拷贝构造 / 赋值重载 / 构造、析构函数 / 运算符重载......
默认生成的、标准库中的 够用,如需特殊优化再处理
迭代器
容器适配器 不提供 迭代器
普通容器实现迭代器的方式:
1、通常写成 内部类(模板嵌套类型),主流 STL 源码(SGI/LLVM/MSVC)普遍使用 容器内部嵌套的 class iterator/class const_iterator
2、有些实现也可能把迭代器写成独立模板,再 typedef 进容器;
测试
#include"myStack.h"int main() {myStack<int> st;st.push(1);st.push(2);st.push(3);while (!st.empty()) {std::cout << st.top() << ' ';st.pop();}
}
queue
手撕
抽象
容器适配器、FIFO、标准底层容器用 deque
骨架
填肉
#include<iostream>
#include<queue>template<class T, class Container = std::deque<T>>
class myQueue {
public:void push(const T& val){_c.push_back();}void pop(){_c.pop();}T& front(){return _c.front();}T& back(){return _c.back();}size_t size(){return _c.size();}bool empty(){return _c.empty;}private:Container _c;
};......
后续步骤 同 容器适配器 stack
仿函数
仿函数(Functor)= “用起来像函数的对象”
在 C++ 里,它指的是 重载了 operator() 的类/结构体实例。
对象后面跟一对括号就能像普通函数那样被调用,因此得名 “function-like object”。
class Add
{
public:int operator()(int x, int y){return x + y;}
};int main()
{Add add;int a = 6, b = 8;cout << "add(a, b) = " << add(a, b) << endl;cout << "add.operator()(a, b) = " << add.operator()(a, b) << endl;return 0;
}
重载了 operator() 的类,调用时 传参方式也是直接放在括号里,这样使其 对象 调用时与函数格式一样;当然,也可以显式调用。
再套上模板:
template<class T>
class Add
{
public:T operator()(T x, T y){return x + y;}
};int main()
{Add<int> add;int a = 6, b = 8;cout << "add(a, b) = " << add(a, b) << endl;cout << "add.operator()(a, b) = " << add.operator()(a, b) << endl;Add<double> addd;double c = 6.6, d = 8.8;cout << "addd(c, d) = " << addd(c, d) << endl;cout << "addd.operator()(c, d) = " << addd.operator()(c, d) << endl;return 0;
}
仿函数 替代了 函数指针的功能,而且相较 函数指针 更有优势:
1、可带状态——普通函数指针做不到“记住”数据,而仿函数可以拥有成员变量。
2、可以作为模板参数——仿函数可以作为模板参数,在 priority_queue 中会用到。STL 算法中 有 大量使用仿函数的策略( std::sort, std::accumulate, std::priority_queue 的自定义比较器)。
3、内联友好——函数对象通常是轻量级类,编译器易于内联,效率高于函数指针。
注:C++11 起,lambda 表达式会被编译器自动生成一个匿名仿函数类
所以:仿函数 = 重载了 operator() 的类,用起来像函数,却能携带状态和类型信息,是 STL 算法与 lambda 的底层基石。
priority_queue

优先级队列(抽象数据类型),底层默认是个堆(具体数据结构),大堆 —— 因为 类模板参数中有仿函数 less 的原因
标准库中的 优先级队列,默认使用 vector 适配生成
手撕
抽象
底层是堆结构(完全二叉树,父子节点保持大小关系一致),使用 vector 适配
堆结构 意味着:push 操作需要 尾插,并向上调整( O(n*logn) );pop 操作 删除堆顶数据 需要 首尾交换,删掉尾部数据并 向下调整( O(n) )。
骨架
别忘了 在 成员变量中 用 Compare 声明 比较器对象类型 ,我们将用这个比较器 灵活实现 大堆小堆,默认小堆(当然 具体比较逻辑 在 adjust_up、adjust_down 向上调整和向下调整的 函数中实现)
#include<iostream>
#include<vector>template<class T>
class myLess
{
public:bool operator()(const T& x, const T& y) // 实现 () 重载,形成仿函数{}
};template<class T>
class myGreater
{
public:bool operator()(const T& x, const T& y) // 实现 () 重载,形成仿函数{}
};template<class T, class Container = std::vector<T>, class Compare = myLess<T>>
class mmyPriority
{
public:void adjust_up(size_t child) // push 需要向上调整,传入 孩子 下标(即 尾插后的 最后一个元素 下标){}void push(const T& val){}void adjust_down(size_t parent) // pop 需要向下调整,传入 父亲 下标(即 首尾交换过后,堆顶元素下标 0){}void pop() // 删除堆顶元素{}T& top(){}size_t size(){}bool empty(){}
private:Container _c;Compare _com; // 比较器对象,仿函数
};填肉
template<class T>
class myLess
{
public:bool operator()(const T& x, const T& y) // 实现 () 重载,形成仿函数{return x < y;}
};template<class T>
class myGreater
{
public:bool operator()(const T& x, const T& y) // 实现 () 重载,形成仿函数{return x > y;}
};template<class T, class Container = std::vector<T>, class Compare = myLess<T>>
class mmyPriority
{
public:void adjust_up(size_t child) // push 需要向上调整,传入 孩子 下标(即 尾插后的 最后一个元素 下标){}void push(const T& val){_c.push_back(val); // 尾插adjust_up(_c.size() - 1); // 向上调整 最后一个元素}void adjust_down(size_t parent) // pop 需要向下调整,传入 父亲 下标(即 首尾交换过后,堆顶元素下标 0){}void pop() // 删除堆顶元素{std::swap(_c[0], _c[_c.size() - 1]); // 交换 堆顶 堆底 元素,用了 std 提供的全局 swap_c.pop_back(); // 删除 堆底 元素adjust_down(0); // 堆顶元素 向下调整,维持 堆序}const T& top() const{return _c[0];}size_t size() const{return _c.size();}bool empty() const{return _c.empty();}
private:Container _c;Compare _com; // 比较器对象,仿函数
};重点关注 重温 堆 的 向上调整 和 向下调整 实现:
adjust_up 向上调整
对一个堆进行尾插,并传入最后一个元素下标 child,判断是否需要调整:
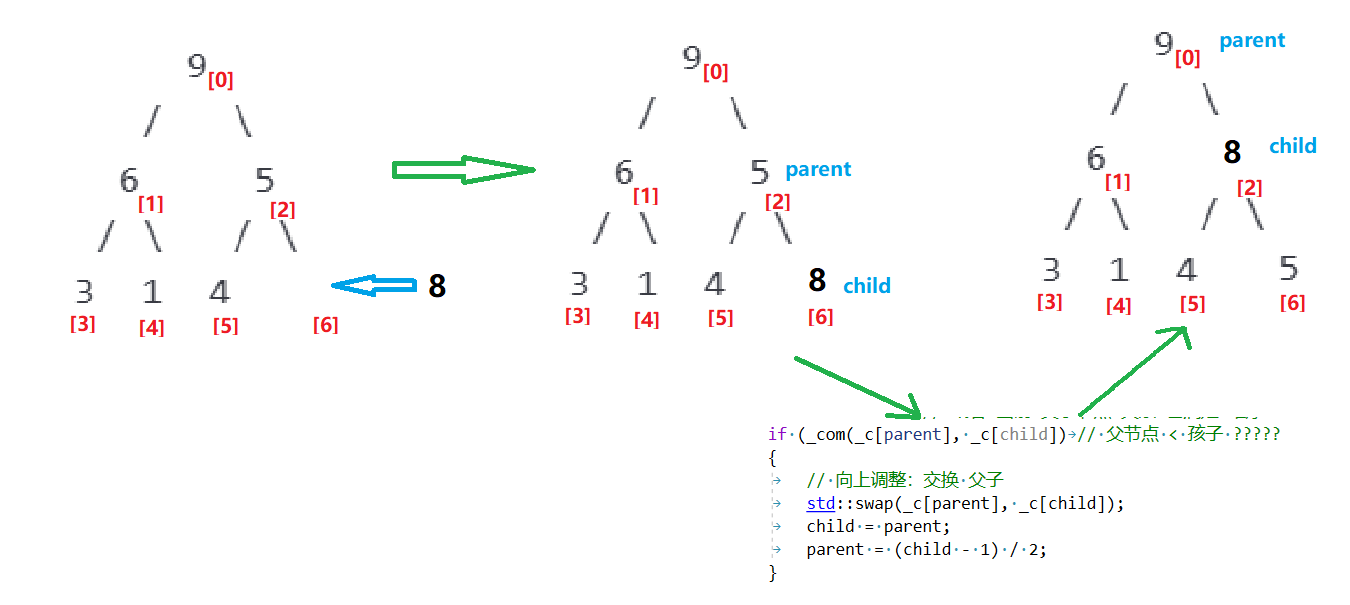
void adjust_up(size_t child) // push 需要向上调整,传入 孩子 下标(即 尾插后的 最后一个元素 下标)
{size_t parent = (child - 1) / 2; // 计算 父节点 下标while (child > 0) // 循环结束条件:孩子节点一直向上调整到了 根 的位置{ // 或者 当前 父子节点 关系 已满足 堆序if (_com(_c[parent], _c[child]) // 父节点 < 孩子 ?????{// 向上调整:交换 父子std::swap(_c[parent], _c[child]);child = parent;parent = (child - 1) / 2;}else{// 已满足堆序break;}}
}adjust_down 向下调整
删除堆顶元素:交换首尾元素后 删掉尾部元素,并将 堆顶元素 向下调整
向下调整:判断父节点 是否已经 大于 左右孩子中的较大者
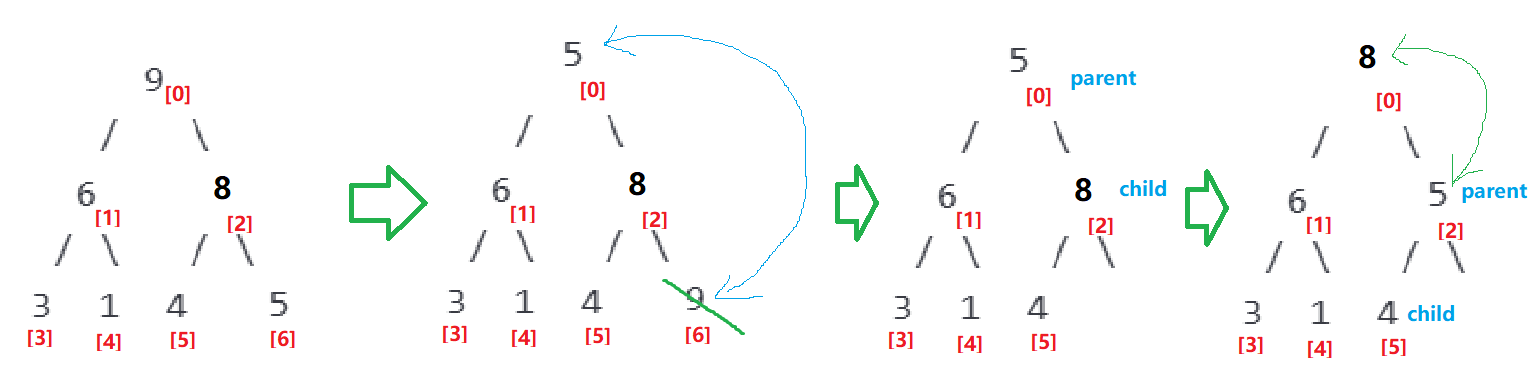
void adjust_down(size_t parent) // pop 需要向下调整,传入 父亲 下标(即 首尾交换过后,堆顶元素下标 0)
{size_t child = parent * 2 + 1; // 左孩子while (child < _c.size()) // 循环结束条件:child 仍在容器范围内{ // 或者 当前 父子节点已满足 堆序if (child + 1 < _c.size() && _com(_c[child], _c[child + 1])) // 如果 右孩子 存在,且 右孩子 > 左孩子{child++; // 让右孩子 成为 最大的孩子,接下来与 父节点 比较,是否需要调整}if (_com(_c[parent], _c[child])) // 父节点 < 孩子 ? 调整 : break{std::swap(_c[parent], _c[child]); // 交换 父子parent = child;child = parent * 2 + 1;}else{break;}}
}其实还有一种 粗暴的写法更为简洁并且 可读性更高:直接 两两判断父节点和两个孩子的关系(如果孩子存在):
void adjust_down(size_t parent)
{size_t n = _c.size();while (true){size_t largest = parent; // 假设 父节点 最大size_t left = 2 * parent + 1;size_t right = 2 * parent + 2;if (left < n && _com(_c[largest], _c[left])) largest = left;if (right < n && _com(_c[largest], _c[right])) largest = right;if (largest == parent) break;std::swap(_c[parent], _c[largest]);parent = largest;}
}异常
有越界访问 或者 堆空时删除的操作,底层容器 vector 中已经处理。
拷贝构造 / 赋值重载 / 构造、析构函数 / 运算符重载......
默认生成的、标准库中的 够用,如需特殊优化再处理
迭代器
容器适配器 不提供 迭代器
优先级队列 限制了 只暴露 操作 首元素(堆顶元素)的接口;如果想要遍历元素 等操作内部任意元素,那么 堆 这种 结构,才会提供这种接口
测试
#include"mmyPriority_queue.h"
using namespace std;void test_priority_queue()
{mmyPriority_queue<int> pq;pq.push(1);pq.push(3);pq.push(5);pq.push(2);pq.push(68);pq.push(99);pq.push(55);pq.push(0);while (!pq.empty()){cout << pq.top() << " ";pq.pop();}cout << endl;
}int main()
{test_priority_queue();return 0;
}
补充:序列容器 deque

双端队列 两端都可以在 O(1) 时间内完成插入/删除,且支持随机访问;
并非 受到队列一样 FIFO 的限制;
内部结构:
分块链表 + 索引表(中央控制器 + 若干固定大小的 buffer)。
逻辑上连续,物理上分块,因此迭代器比 vector 复杂,但依然满足 RandomAccessIterator。
