第5章 学习的机制
主要内容:
理解算法如何从数据中学习
使用微分和梯度下降法,将学习重构为参数估计
了解一个简单学习算法
了解
PyTorch如何支持自动求导
5.1 永恒的建模经验
开普勒考虑了多个可能符合手头数据的候选模型,最终确定为一个椭圆:
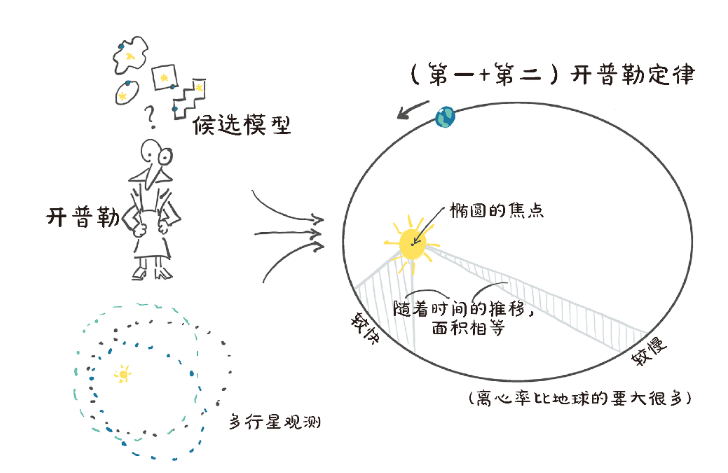
要确定这个,开普勒尝试不同的形状,使用一定数量的观察值来找到曲线,然后利用曲线找到更多位置,在他有观测数据的时候,检查这些计算出的位置是否与观察到的位置一致。
5.2 学习就是参数估计
学习获取数据、选择模型并估计模型的参数,以便它能够对新数据做出良好的预测。
机器学习:
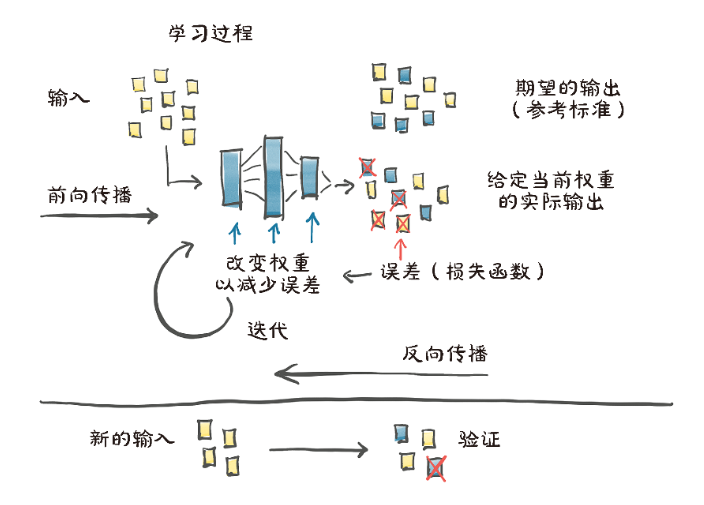
给定输入数据和相应的期望输出(实际数据),以及权重的初始值,给模型输入数据(正向传播),并通过对输出结果与实际数据进行比较来评估误差。为了优化模型参数,即它的权重,权重单位变化后的误差编码(误差相对参数的梯度)是使用复合函数的导数的链式法则计算的(反向传播)。然后,在使误差减小的方向上更新权重值。重复该过程,知道根据未知的数据评估的误差降到可接受的水平。
学习过程的心智模型:
5.2.1 一个热点问题
抛开纷繁难懂的行星运动,把注意力转移到物理学中第2难得问题上:校准仪器。
我们刚从一个地方旅游回来,带回了一个别致的壁挂式模拟温度计。它看起来很棒,而且非常适合我们的客厅,唯一的缺点是不显示单位。
我们将建立一个数据集,以我们选择的单位来表示刻度值和相应的温度值,选择一个模型,迭代地调整它的权重,直到误差的度量足够低,最终能够以我们选择的单位来解释新的刻度值。
5.2.2 收集一些数据
%matplotlib inline
import numpy as np
import torch
torch.set_printoptions(edgeitems=2, linewidth=75)t_c = [0.5, 14.0, 15.0, 28.0, 11.0, 8.0, 3.0, -4.0, 6.0, 13.0, 21.0]
t_u = [35.7, 55.9, 58.2, 81.9, 56.3, 48.9, 33.9, 21.8, 48.4, 60.4, 68.4]
t_c = torch.tensor(t_c)
t_u = torch.tensor(t_u)t_c 值是以摄氏度为单位的温度,而 t_u 值是我们未知的单位。
5.2.3 可视化数据
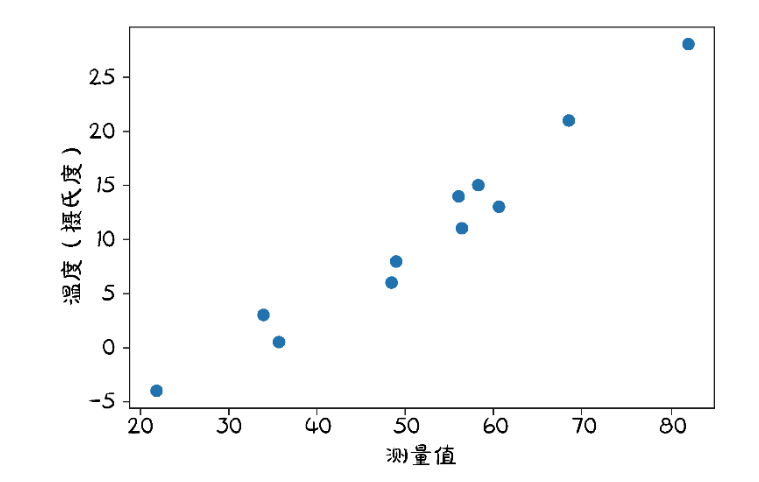
有规律,但是有噪声。
5.2.4 选择线性模型首试
在缺乏进一步了解的情况下,我们假设了一个用于2组测量数据转换的最简单的模型,就像开普勒所做的那样。这2个测量数据集可能是线性相关的——也就是说,将 t_u 乘一个因子,再加一个常数,我们可以得到摄氏温度(忽略一定误差)。
t_c = w * t_u + b将权重和偏置分别命名为 w 和 b ,优化的过程以找到 w 和 b 为目标,使损失函数的值处于最小值。
使用 PyTorch 来完成这个简单的例子,同时我们也意识到训练神经网络本质上是使用几个或一些参数将一个模型变换为更加复杂的模型。
5.3 减少损失是我们想要的
损失函数(或代价函数)是一个计算单个数值的函数,学习过程将试图使其值最小化。损失的计算通常涉及获取一些训练样本的期望输出与输入这些样本时模型实际产生的输出之间的差值。在我们的例子中,它将是模型输出的预测温度t_p与实际测量值之间的差值,即t_p−t_c。
最直接的是:
|t_p−t_c| 和 (t_p−t_c)2
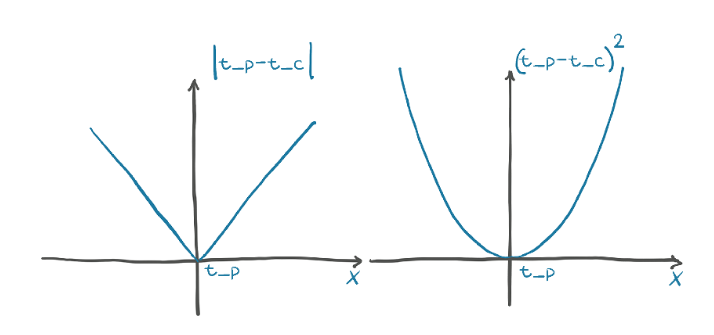
对于两个损失函数,我们注意到误差的平方在最小值附近表现得更好:当 t_p = t_c 时,误差平方损失对 t_p的导数为0。另外,绝对值在我们要收敛的地方有一个不明确的导数。
值得注意的是,平方差比绝对差对错误结果的惩罚更大。通常,有更多轻微错误的结果比有少量严重错误的结果要好,并且平方差有助于根据需要优先处理相关问题。
示例解释:
假设我们有一个预测值 t_p 和一个真实值 t_c。为了简单起见,我们设 t_c = 0,然后观察 t_p 在不同值时,两种损失函数的值和导数。
损失函数定义:
绝对值损失函数:
L1 = |t_p - t_c| = |t_p|平方损失函数:
L2 = (t_p - t_c)^2 = t_p^2
绘图分析:
损失函数值随
t_p的变化
绝对值损失:当
t_p远离0时,损失线性增长;当t_p接近0时,损失逐渐减小到0。平方损失:当
t_p远离0时,损失以平方的速度增长;当t_p接近0时,损失也逐渐减小到0,但曲线更“陡峭”。
导数随
t_p的变化
绝对值损失的导数:
当
t_p > 0时,导数为1。当
t_p < 0时,导数为-1。当
t_p = 0时,导数不明确(或说是不连续的)。
平方损失的导数:
导数为
2 * t_p。当
t_p = 0时,导数为0,且在这个点附近是平滑的。
绝对值损失导数: -1 (t_p < 0) | 1 (t_p > 0)------------0------------平方损失导数: .. .. .(在t_p=0时为0,且平滑)实际应用示例
假设我们有一个回归问题,预测房价。真实房价是100万。
使用平方损失:
如果预测为90万,错误是10万,损失是
(10)^2 = 100(单位:万平方,这里只是示意)。如果预测为50万,错误是50万,损失是
(50)^2 = 2500。平方损失对大错误的惩罚更重。
使用绝对值损失:
如果预测为90万,错误是10万,损失是
|10| = 10。如果预测为50万,错误是50万,损失是
|50| = 50。绝对值损失对所有大小的错误给予相同的线性惩罚。
总结
平方损失:在最小值附近导数平滑,易于优化;对大错误惩罚更重,适合希望减少大错误的场景。
绝对值损失:在最小值附近导数不连续,可能影响优化;对所有错误给予相同的线性惩罚,适合需要均匀处理所有错误的场景。
从问题回到 PyTorch
定义模型:
def model(t_u, w, b):return w * t_u + b我们期望t_u、w和b分别作为输入张量、权重参数和偏置参数。
定义损失函数:
先对其平方元素进行处理,最后通过对得到的张量中的所有元素求平均值得到一个标量损失函数,即均方损失函数。
def loss_fn(t_p, t_c):squared_diffs = (t_p - t_c)**2return squared_diffs.mean()初始化参数,调用模型:
w = torch.ones(())
b = torch.zeros(())t_p = model(t_u, w, b)
t_p# Out
tensor([35.7000, 55.9000, 58.2000, 81.9000, 56.3000, 48.9000, 33.9000,21.8000, 48.4000, 60.4000, 68.4000])检查损失的值:
loss = loss_fn(t_p, t_c)
loss# Out
tensor(1763.8848)如何估计 w 和 b ,以使损失达到最小?
扩展:广播机制
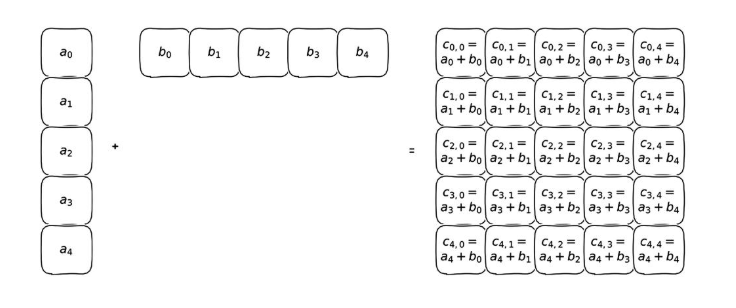
如果一个张量的维度大于另一个张量的维度,那么另一个张量上的所有项将和这些维度上的每一项进行运算。
PyTorch 的广播机制(broadcasting mechanism)允许对不同形状的张量进行二元运算(如加法、减法、乘法、除法等),而不需要显式地调整它们的形状。这种机制通过自动扩展较小张量的形状,使其与较大张量的形状匹配,从而简化运算。
示例:
考虑以下两个张量:
张量
A的形状为(5, 1)张量
B的形状为(1, 5)
假设我们要计算 A + B。
维度对齐:
A的形状是(5, 1),B的形状是(1, 5)。由于
A的第二个维度是1,而B的第二个维度是5,A的第二个维度会被扩展为5。由于
B的第一个维度是1,而A的第一个维度是5,B的第一个维度会被扩展为5。
广播后的形状:
经过广播后,
A和B的形状都变为(5, 5)。
运算:
每个位置上的元素相加,得到结果张量
C,其形状为(5, 5)。
实际应用:
广播机制在深度学习中非常有用,例如:
添加偏置:在神经网络中,偏置项通常是一个一维张量,可以通过广播机制添加到二维的权重矩阵上。
归一化:在数据预处理中,可以通过广播机制对每个样本应用相同的归一化因子。
5.4 沿着梯度下降
根据参数使用梯度下降法来优化损失函数。
心智图像:优化过程的一个卡通描绘,一个人旋转 w 和 b 旋钮,寻找使损失减小的方向。
5.4.1 减小损失
1.梯度下降的核心思想
梯度下降的目标是最小化损失函数(即模型的预测误差)。
损失函数
loss_fn衡量模型预测值与真实值之间的差距。模型参数(如
w和b)需要调整,使得损失函数尽可能小。
梯度下降的做法:
计算损失函数对参数的变化率(梯度)。
沿着梯度反方向调整参数(因为梯度指向损失增大的方向,反方向是损失减小的方向)。
重复这个过程,直到损失足够小或不再变化。
2.数值微分法计算梯度
delta = 0.1 # 一个小数字,用于近似微分# 计算 w 的梯度(损失对 w 的变化率)
loss_rate_of_change_w = \(loss_fn(model(t_u, w + delta, b), t_c) - # w 增加 delta 时的损失loss_fn(model(t_u, w - delta, b), t_c)) / (2.0 * delta) # w 减少 delta 时的损失解释:
(f(x+Δ) - f(x-Δ)) / (2Δ)是中心差分公式,用于近似导数。这里计算的是损失函数对
w的变化率(即梯度)。
3.参数更新
计算梯度后,用学习率(learning_rate)调整参数:
learning_rate = 1e-2 # 通常是一个小数字,如 0.01w = w - learning_rate * loss_rate_of_change_w # 沿梯度反方向更新 w参数更新公式:
w = w - learning_rate * loss_rate_of_change_wloss_rate_of_change_w是损失函数对w的梯度(即变化率)。梯度方向是损失函数增大的方向,因此我们要沿梯度反方向更新参数(即
-号)。学习率乘以梯度,得到一个较小的调整量,确保参数更新不会太大。
数学上,梯度下降的更新公式是:
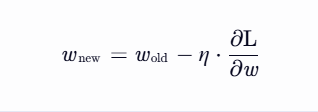
梯度方向是损失函数增大的方向。
我们希望减小损失,所以必须沿梯度反方向更新参数(即
-号)。
4.示例
假设:
当前
w = 1.0梯度
loss_rate_of_change_w = 0.5(意味着如果w增加 1,损失会增加 0.5)学习率
learning_rate = 0.01
更新过程:
w_new = w_old - learning_rate * gradient= 1.0 - 0.01 * 0.5= 1.0 - 0.005= 0.995新的 w 是 0.995,比原来的 1.0 更接近最优解(假设最优解在 w 更小的方向)。
5.总结
学习率控制参数更新的步长,避免跳过最优解或收敛太慢。
梯度方向是损失增大的方向,因此要沿梯度反方向更新参数(
w - ...)。梯度下降的目标是逐步调整参数,使损失最小化。
对 b 采用与 w 相同的处理方式:
loss_rate_of_change_b = \(loss_fn(model(t_u, w, b + delta), t_c) - loss_fn(model(t_u, w, b - delta), t_c)) / (2.0 * delta)b = b - learning_rate * loss_rate_of_change_b6.梯度下降的直观理解
想象你在爬山,目标是下山(最小化损失)。
梯度告诉你当前位置最陡的下山方向。
学习率是你每一步迈多大的步子。
重复这个过程,最终你会到达山底(损失最小值)。
5.4.2 进行分析
当在离散的位置进行评估与对比分析时,估计下降方向的差异:
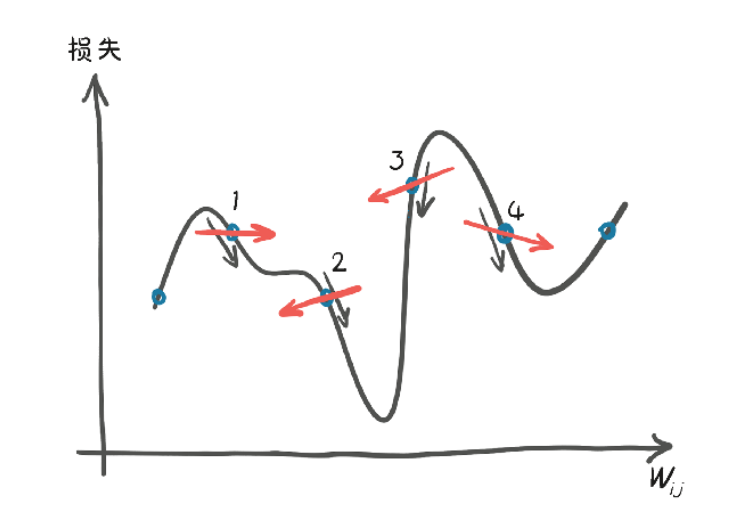
下面是关于如何计算损失函数对模型参数梯度(即导数),以便进行梯度下降优化。
我们需要计算损失函数 loss_fn 对参数 w 和 b 的梯度(即导数),以便知道如何调整参数来减小损失。
数学公式
根据链式法则:
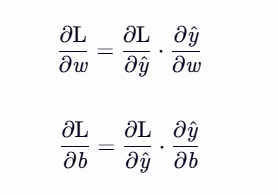
其中:
L 是损失函数(
loss_fn)。y^ 是模型的预测值(
model(t_u, w, b))。
2.代码解析
(1)损失函数 loss_fn
def loss_fn(t_p, t_c):squared_diffs = (t_p - t_c)**2return squared_diffs.mean()(2)损失函数对预测值的导数dloss_fn
def dloss_fn(t_p, t_c):dsq_diffs = 2 * (t_p - t_c) / t_p.size(0) # 均值的导数return dsq_diffs(3)模型
def model(t_u, w, b):return w * t_u + b(4)模型对参数的导数
def dmodel_dw(t_u, w, b):return t_u # ∂ŷ/∂w = t_udef dmodel_db(t_u, w, b):return 1.0 # ∂ŷ/∂b = 1(5)梯度计算函数 grad_fn
def grad_fn(t_u, t_c, t_p, w, b):dloss_dtp = dloss_fn(t_p, t_c) # ∂L/∂ŷdloss_dw = dloss_dtp * dmodel_dw(t_u, w, b) # ∂L/∂w = ∂L/∂ŷ * ∂ŷ/∂wdloss_db = dloss_dtp * dmodel_db(t_u, w, b) # ∂L/∂b = ∂L/∂ŷ * ∂ŷ/∂breturn torch.stack([dloss_dw.sum(), dloss_db.sum()])dloss_dtp:损失对预测值的导数(∂y^∂L)。dloss_dw:损失对w的导数(∂w∂L),由链式法则计算。dloss_db:损失对b的导数(∂b∂L)。torch.stack:将梯度合并成一个张量,方便后续使用。
5.4.3 迭代以适应模型
现在我们已经做好了优化参数的准备。从某参数的假定值开始,我们可以对它应用更新,进行固定次数的迭代,或者直到w和b停止变化为止。有一些让迭代停止的条件,这里我们还是采用固定次数的迭代。
我们称训练迭代为一个迭代周期(epoch),在这个迭代周期,我们更新所有训练样本的参数。
1.梯度下降训练循环
def training_loop(n_epochs, learning_rate, params, t_u, t_c):for epoch in range(1, n_epochs + 1):w, b = paramst_p = model(t_u, w, b) # 正向传播:计算预测值loss = loss_fn(t_p, t_c) # 计算损失grad = grad_fn(t_u, t_c, t_p, w, b) # 反向传播:计算梯度params = params - learning_rate * grad # 更新参数print('Epoch %d, Loss %f' % (epoch, float(loss)))return params正向传播:计算模型预测值
t_p = w * t_u + b。损失计算:计算预测值与真实值的均方误差(MSE)。
反向传播:计算损失对参数
w和b的梯度。参数更新:沿梯度反方向调整参数,学习率控制步长。
2.实验1:学习率过大导致参数爆炸
输出结果
Epoch 1, Loss 1763.884644Params: tensor([-44.1730, -0.8260])Grad: tensor([4517.2969, 82.6000])
Epoch 2, Loss 5802485.500000Params: tensor([2568.4014, 45.1637])Grad: tensor([-261257.4219, -4598.9712])
...
Epoch 10, Loss 90901154706620645225508955521810432.000000Params: tensor([3.2144e+17, 5.6621e+15])问题:学习率
1e-2过大,导致参数更新步长太大,损失和参数值迅速爆炸(变成inf)。原因:梯度值很大(如
4517.2969),乘以学习率后,参数更新量过大,导致模型不稳定。
3.实验2:降低学习率使训练稳定
输出结果:
Epoch 1, Loss 1763.884644Params: tensor([ 0.5483, -0.0083])
Epoch 2, Loss 323.090546Params: tensor([ 0.3623, -0.0118])
...
Epoch 100, Loss 29.022669Params: tensor([ 0.2327, -0.0438])解决方案:将学习率降低到
1e-4。效果:
参数更新步长变小,训练稳定。
损失逐渐减小,最终收敛到某个值(如
29.022669)。
问题:虽然训练稳定,但收敛速度较慢(需要更多迭代)。
4.实验3:输入归一化
t_un = 0.1 * t_u # 归一化输入:将 t_u 缩小 10 倍输出结果:
Epoch 1, Loss 80.364342Params: tensor([1.7761, 0.1064])
Epoch 2, Loss 37.574917Params: tensor([2.0848, 0.1303])
...
Epoch 100, Loss 22.148710Params: tensor([ 2.7553, -2.5162])为什么归一化?
原始输入
t_u的数值较大(如200),导致模型输出t_p = w * t_u + b数值也很大。梯度
∂L/∂w = (2/N) * (t_p - t_c) * t_u也会很大,导致参数更新不稳定。
归一化后:
输入
t_un的数值范围变小(如20.0→2.0)。梯度值变小,参数更新更稳定。
即使学习率调回
1e-2,训练也不会爆炸。
5.长期训练结果
Epoch 5000, Loss 2.927648Params: tensor([ 5.3671, -17.3012])归一化后,模型可以长期训练,损失进一步降低。
5.4.5 再次可视化数据
# In:
%matplotlib inline
from matplotlib import pyplot as pltt_p = model(t_un, *params) ⇽--- 记住,我们正在对归一化的未知部分进行训练。我们也使用参数解包fig = plt.figure(dpi=600)
plt.xlabel("Temperature (°Fahrenheit)")
plt.ylabel("Temperature (°Celsius)")
plt.plot(t_u.numpy(), t_p.detach().numpy()) ⇽--- 但是我们画的是原始的未知数
plt.plot(t_u.numpy(), t_c.numpy(), 'o')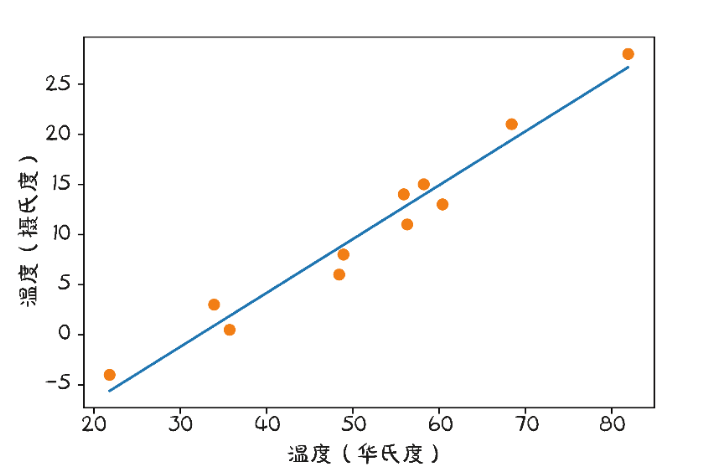
5.5 PyTorch自动求导:反向传播的一切
PyTorch 的自动微分(Autograd)机制,它能够自动计算梯度,无需手动推导。
1.自动微分(Autograd)的核心思想
PyTorch张量可以记录它们的计算历史(即如何从其他张量生成)。如果一个张量设置了
requires_grad=True,PyTorch会跟踪所有涉及该张量的操作,构建一个计算图。调用
.backward()时,PyTorch会反向遍历计算图,自动计算梯度并存储在.grad属性中。
2.代码解析
(1)定义模型和损失函数
def model(t_u, w, b):return w * t_u + bdef loss_fn(t_p, t_c):squared_diffs = (t_p - t_c)**2return squared_diffs.mean()模型:线性回归模型
ŷ = w * x + b。损失函数:均方误差(MSE)。
(2)初始化参数并启用自动微分
params = torch.tensor([1.0, 0.0], requires_grad=True)requires_grad=True告诉PyTorch跟踪涉及params的所有操作,以便后续计算梯度。
(3)计算损失并反向传播
loss = loss_fn(model(t_u, *params), t_c)
loss.backward() # 反向传播,计算梯度
print(params.grad) # 输出梯度loss.backward():反向遍历计算图,计算
loss对params的梯度。梯度存储在
params.grad中。
输出:
tensor([4517.2969, 82.6000])梯度值与之前手动计算的梯度一致,验证了自动微分的正确性。
(4)梯度累加问题
问题:如果多次调用
loss.backward(),梯度会累加(而不是覆盖)。解决方案:在每次迭代前清零梯度:
if params.grad is not None:params.grad.zero_()(5)完整的训练循环
def training_loop(n_epochs, learning_rate, params, t_u, t_c):for epoch in range(1, n_epochs + 1):# 清零梯度if params.grad is not None:params.grad.zero_()# 正向传播t_p = model(t_u, *params)loss = loss_fn(t_p, t_c)# 反向传播loss.backward()# 更新参数(需要暂时关闭梯度计算)with torch.no_grad():params -= learning_rate * params.grad# 打印日志if epoch % 500 == 0:print('Epoch %d, Loss %f' % (epoch, float(loss)))return paramsrequires_grad=True:启用梯度跟踪。loss.backward():反向传播,计算梯度。params.grad.zero_():清零梯度,防止累加。with torch.no_grad()::临时关闭梯度计算,用于参数更新。
(6)运行训练
training_loop(n_epochs=5000,learning_rate=1e-2,params=torch.tensor([1.0, 0.0], requires_grad=True),t_u=t_un, # 归一化后的输入t_c=t_c)输出:
Epoch 500, Loss 7.860116
Epoch 1000, Loss 3.828538
...
Epoch 5000, Loss 2.927647损失逐渐减小,参数收敛到合理值。
5.5.2 优化器
torch模块有一个optim子模块,我们可以在其中找到实现不同优化算法的类。
# In:
import torch.optim as optimdir(optim)# Out:
['ASGD','Adadelta','Adagrad','Adam','Adamax','LBFGS','Optimizer','RMSprop','Rprop','SGD','SparseAdam',
...
]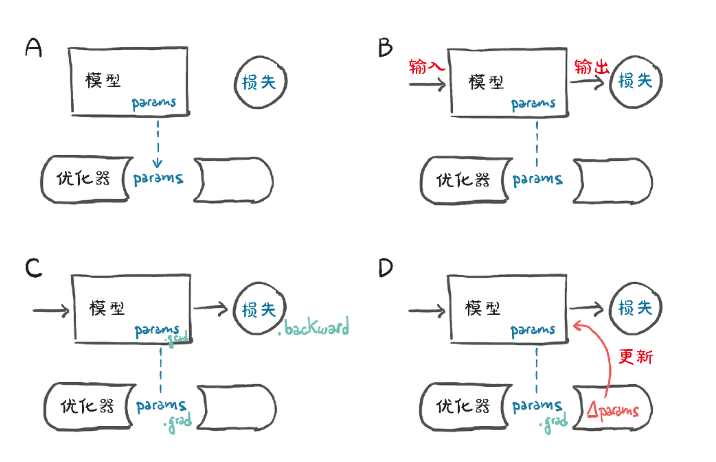
1.优化器的作用
优化器(
Optimizer)的作用是:访问参数的梯度(通过
.grad属性)。根据梯度更新参数,以最小化损失函数。
常见的优化算法:
SGD(随机梯度下降):最基础的优化器,按梯度方向更新参数。
Adam:自适应学习率优化器,结合了动量(
Momentum)和RMSProp的思想。RMSprop:适用于非平稳目标的优化器,常用于 RNN。
2.代码解析
(1)初始化优化器
import torch.optim as optimparams = torch.tensor([1.0, 0.0], requires_grad=True)
learning_rate = 1e-5
optimizer = optim.SGD([params], lr=learning_rate) # 使用 SGD 优化器optim.SGD:接收参数列表(
[params])和学习率(lr)。优化器会跟踪这些参数的梯度,并在
step()时更新它们。
(2)计算损失并反向传播
t_p = model(t_u, *params) # 正向传播
loss = loss_fn(t_p, t_c) # 计算损失
loss.backward() # 反向传播,计算梯度loss.backward():计算损失对参数的梯度,存储在
params.grad中。
(3)优化器更新参数
optimizer.step() # 更新参数:params = params - lr * gradoptimizer.step():
读取
params.grad,按梯度方向更新参数。相当于手动实现:
with torch.no_grad():params -= learning_rate * params.grad(4)清零梯度
optimizer.zero_grad() # 清零梯度,防止累加为什么需要清零梯度?
如果不清零,多次调用
loss.backward()会导致梯度累加(而不是覆盖)。优化器的
zero_grad()方法可以安全地清零梯度。
3.完整的训练循环
def training_loop(n_epochs, optimizer, params, t_u, t_c):for epoch in range(1, n_epochs + 1):# 正向传播t_p = model(t_u, *params)loss = loss_fn(t_p, t_c)# 反向传播前清零梯度optimizer.zero_grad()loss.backward()# 更新参数optimizer.step()# 打印日志if epoch % 500 == 0:print('Epoch %d, Loss %f' % (epoch, float(loss)))return params关键步骤:
清零梯度(
optimizer.zero_grad())。正向传播(计算预测值和损失)。
反向传播(计算梯度,
loss.backward())。更新参数(
optimizer.step())。
5.5.3 训练、验证和过拟合
1.评估训练损失
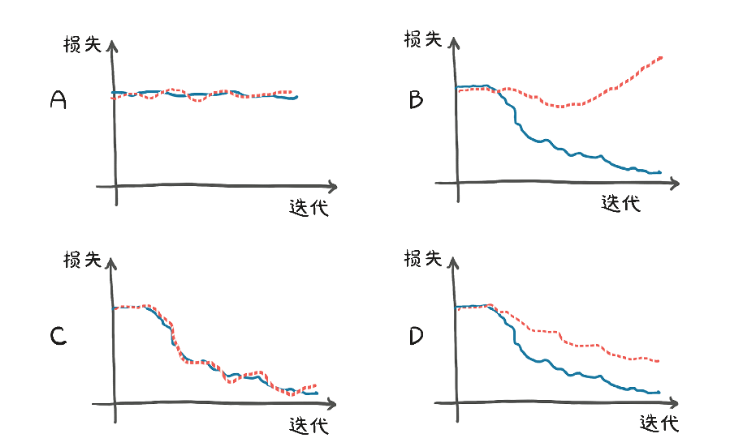
训练损失会告诉我们,我们的模型是否能够完全拟合训练集,换句话说,我们的模型是否有足够的能力处理数据中的相关信息。
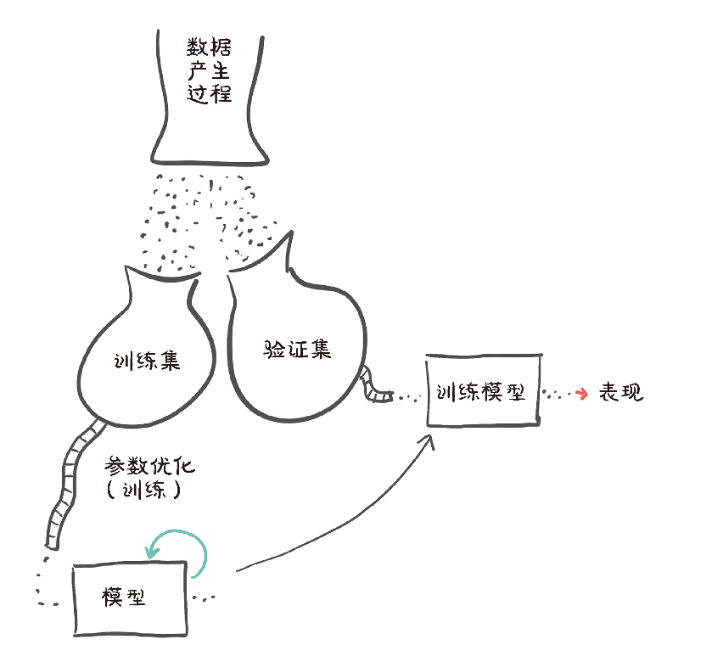
深度神经网络可以潜在地近似复杂的函数,前提是神经元的数量和参数足够多。参数的树木越少,我们的网络所能近似的函数的形状就越简单。所以,规则1:如果训练损失没有减少,一种可能是因为模型对数据来说太简单了。
2.推广到验证集
如果在验证集中评估的损失没有随着训练集的增加而减少,这意味着我们的模型正在改进它在训练过程中看到的样本拟合度,但是它不能推广到这个精确数据集之外的样本。规则2:如果训练损失和验证损失发散,则表明出现了过拟合现象。
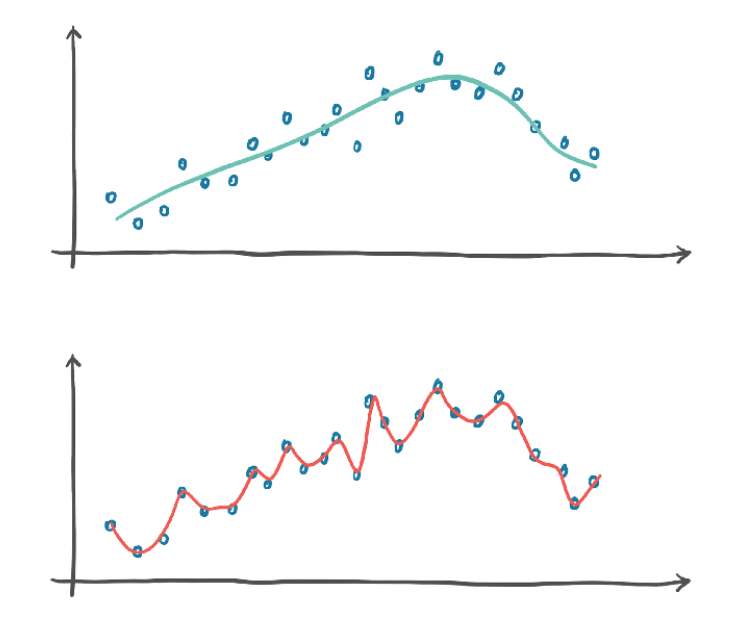
一方面,我们需要模型有足够的能力来拟合训练集。另一方面,我们需要避免模型过拟合。因此,为神经网络模型选择合适的参数的过程分2步:增大参数直到拟合,然后缩小参数直到停止过拟合。
3.分割数据集
把一个张量元素打乱,等于将其元素索引重排列:
# In[12]:
n_samples = t_u.shape[0]
n_val = int(0.2 * n_samples)shuffled_indices = torch.randperm(n_samples)train_indices = shuffled_indices[:-n_val]
val_indices = shuffled_indices[-n_val:]train_indices, val_indices ⇽--- 由于这些值是随机的,所以如果你得到的值与这里打印的值不一样,也不要感到惊讶# Out[12]:
(tensor([9, 6, 5, 8, 4, 7, 0, 1, 3]), tensor([ 2, 10]))得到了索引张量,可以使用索引张量从数据张量开始构建训练集和验证集:
# In[13]:
train_t_u = t_u[train_indices]
train_t_c = t_c[train_indices]val_t_u = t_u[val_indices]
val_t_c = t_c[val_indices]train_t_un = 0.1 * train_t_u
val_t_un = 0.1 * val_t_u训练循环实际上没有改变,只是额外评估每个迭代周期的验证损失,判断是否过拟合:
# In[14]:
def training_loop(n_epochs, optimizer, params, train_t_u, val_t_u,train_t_c, val_t_c):for epoch in range(1, n_epochs + 1):train_t_p = model(train_t_u, *params) ⇽--- train_loss = loss_fn(train_t_p, train_t_c)val_t_p = model(val_t_u, *params) ⇽--- 除了train_*和val_*,这2行代码是相同的val_loss = loss_fn(val_t_p, val_t_c)optimizer.zero_grad()train_loss.backward() ⇽--- 注意,这里没有val_loss.backward(),因为我们不想在验证集上训练模型optimizer.step()if epoch <= 3 or epoch % 500 == 0:print(f"Epoch {epoch}, Training loss {train_loss.item():.4f},"f" Validation loss {val_loss.item():.4f}")return params# In[15]:
params = torch.tensor([1.0, 0.0], requires_grad=True)
learning_rate = 1e-2
optimizer = optim.SGD([params], lr=learning_rate)training_loop(n_epochs = 3000,optimizer = optimizer,params = params,train_t_u = train_t_un, ⇽--- val_t_u = val_t_un,train_t_c = train_t_c, ⇽--- 由于我们再次使用SGD,我们又回到了使用归一化输入val_t_c = val_t_c)# Out[15]:
Epoch 1, Training loss 66.5811, Validation loss 142.3890
Epoch 2, Training loss 38.8626, Validation loss 64.0434
Epoch 3, Training loss 33.3475, Validation loss 39.4590
Epoch 500, Training loss 7.1454, Validation loss 9.1252
Epoch 1000, Training loss 3.5940, Validation loss 5.3110
Epoch 1500, Training loss 3.0942, Validation loss 4.1611
Epoch 2000, Training loss 3.0238, Validation loss 3.7693
Epoch 2500, Training loss 3.0139, Validation loss 3.6279
Epoch 3000, Training loss 3.0125, Validation loss 3.5756tensor([ 5.1964, -16.7512], requires_grad=True)可能出现的训练和验证情况: