深层神经网络

目录

1  深层神经网络

2  深度网络中的前向传播

3  正确处理矩阵尺寸

4  为什么要深度表征？

5  构建深度神经网络模块

6  前向传播和后向传播

7  参数与超参数

8  神经元和大脑

---

1  深层神经网络

        下图的 logistic regression可以说是一个浅层模型；但是对于深层神经网络没有明确的定义，一个隐藏层可以说是深层网络，5个隐藏层也可以说是深层网络。我们在说层数的时候，通常不把输入层计算在内，只考虑隐藏层的层数和输出层。

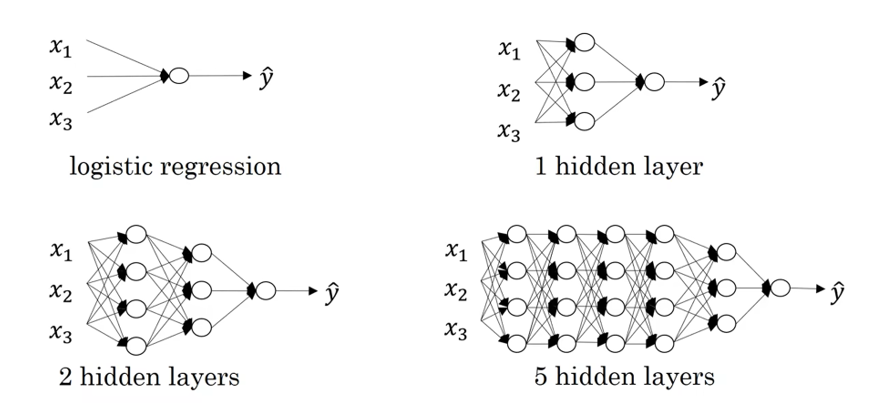
        技术层面上说，逻辑回归是单层神经网络。在有些场景，人们发现只有深层神经网络才可以发挥作用，虽然处理任何具体问题的时候都会很难预先准确地判断需要多深的神经网络，所以可以在一开始先试试逻辑回归是否适合是非常合理的做法，然后试一下两层。

        这是一个四层的神经网络，其中有三个隐藏层和一个输出层，隐藏层中的神经单元数目分别是5,5,3。

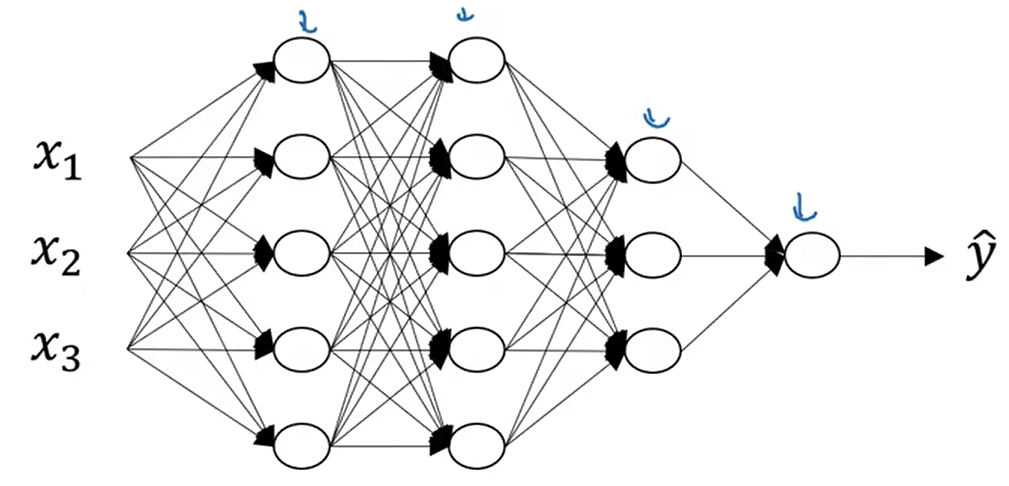
         我们用L来表示神经网络的层数，对这个图来说L=4；

        表示第i层上的神经单元数，对于第一层表示第一层隐藏层有5个神经单元，表示第二层隐藏层有5个神经单元，表示第三层隐藏层有3个神经单元，表示输出层有1个神经单元。对于输入层；

        用表示第i层的激活函数，在前向传播中要计算的；

        表示在中计算的权重；表示在中计算的权重；

        输入特征用x表示，但x也是第0层的激活函数，那么；

        输出层的，也就是说等于预测输出

2  深度网络中的前向传播

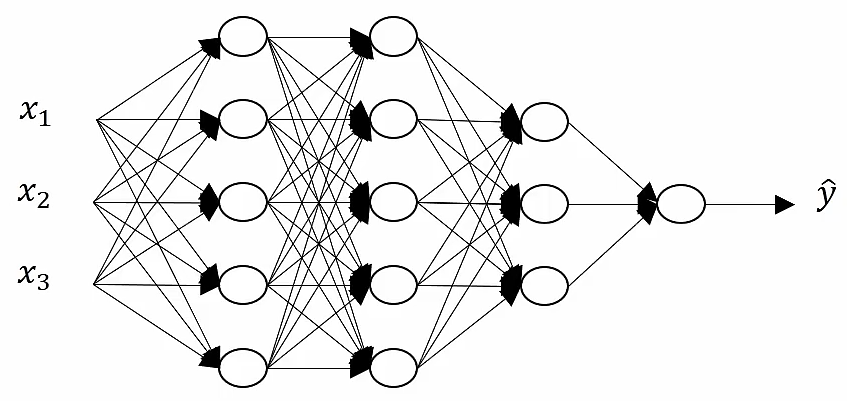
        假设给定一个单一的训练样本x，计算第一个隐藏层的激活函数， ；第二层的激活函数：，；第三层的激活函数：，；输出层的计算是：，

        对于L层的神经网络的最后一层输出公式就是：，

        对于整个训练集也可以这样计算，但只不过每层的z和a是一个按列堆叠的矩阵

3  正确处理矩阵尺寸

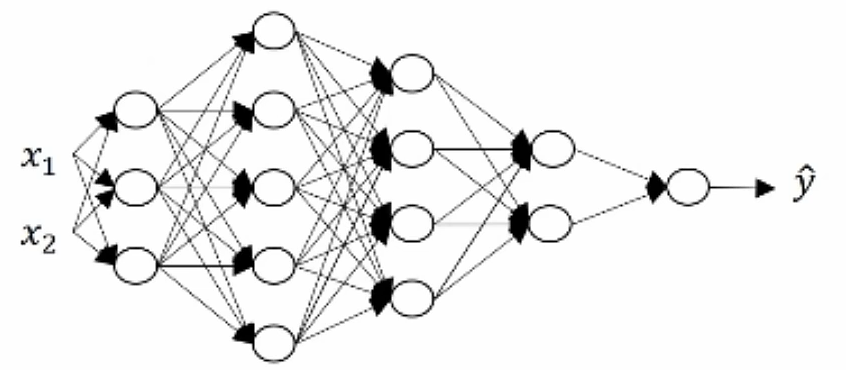
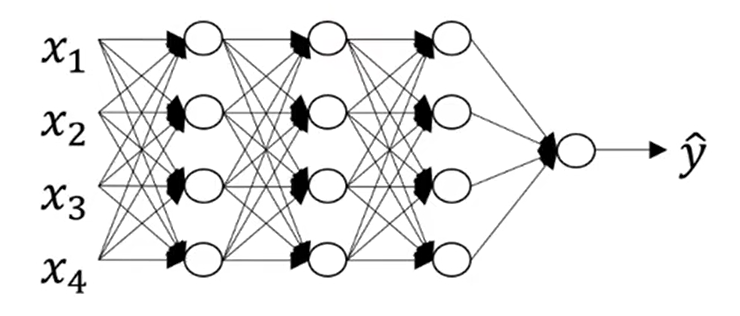
        这是一个5层神经网络，其中4层隐藏层，1层输出层。采用前向传播时，

        对于单样本，我们思考一下z,w和x的维度，z是第一层激活函数向量，z的维度是(3,1)，也就是()，即(特征数，样本数)；x有两个输入特征，所以x的维度是(2,1)，也就是()；w的维度是(3,2)，也就是()  ，即（神经元数，特征数）。

        当有m个训练样本时，。w的维度是(3,2)  () ；x的维度是(2,m)，()；z的维度是(3,m) ()

4  为什么要深度表征？

        我们都听说过深度学习对于很多问题都很有效，而它们不仅仅需要是大型的神经网络。具体而言，它们需要是深度的或者是有很多隐藏层的。我们看几个例子感受下。

        如果我们搭建一个系统用于面部识别，那么神经网络就可以在此运用。输入一张面部图片，那么神经网络的第一层可以被我们认为是一个特征检测器。 

        在这个例子中，我会建一个大约具有20个隐藏神经元的神经网络，看看是怎么针对这张图进行计算的，隐藏单元就是图中的这些小方块。

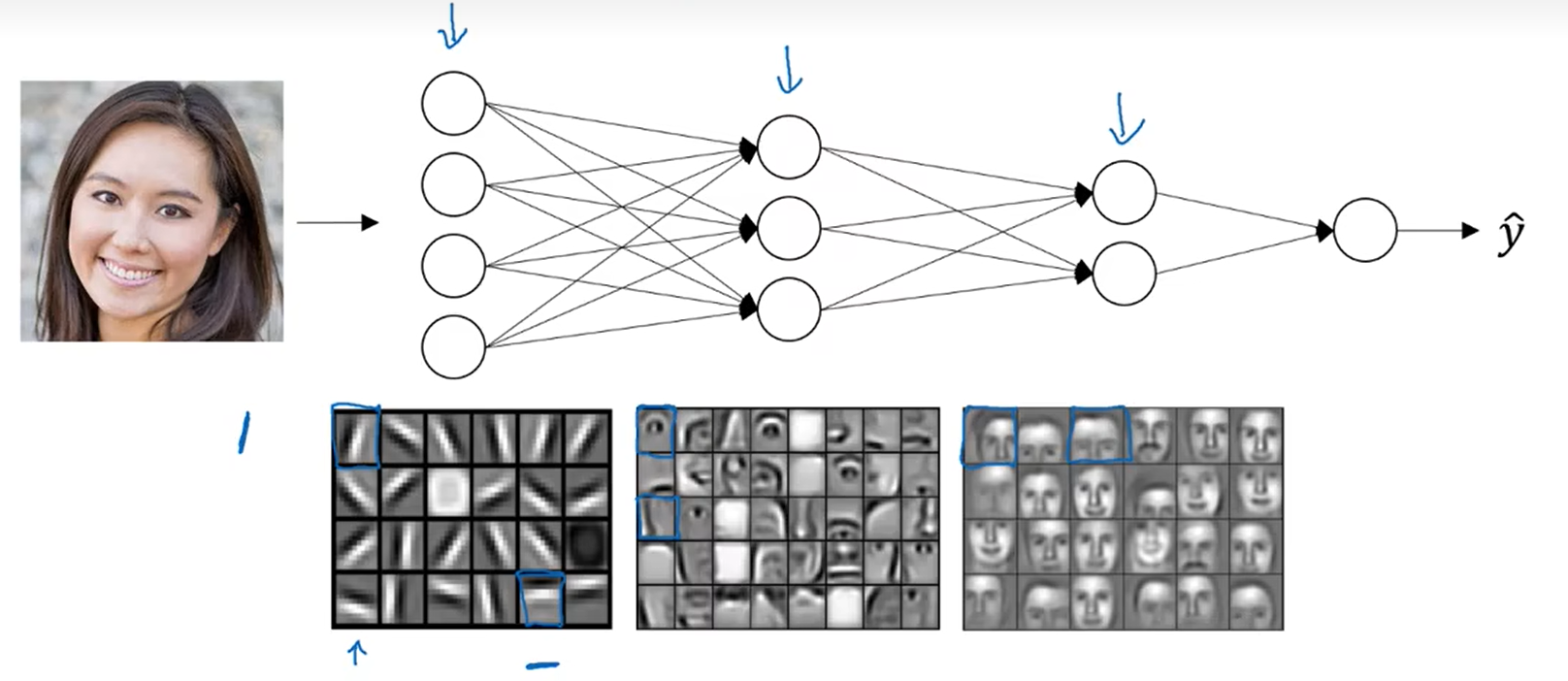
        图中的每个小方块就是一个隐藏单元，它会去找图片里边缘的方向，形式上我们认为神经网络的第一层就好比看一张图片，并尝试找出这张图片的边缘部分；我们可以把照片里组成边缘的像素放在一起看，然后可以别探测到的边缘组成面部的不同部分，比如说可能有一个神经元会去找眼睛的部分，另一个神经元可能找鼻子的部分，把这些边缘结合在一起，就可以开始检测人脸的不同部分；最后再把这些部分放在一起，就可以识别或是探测不同的人脸了。

        你可以直觉上把这种神经网络的前几层当做探测简单的函数，之后再把他们跟后几层结合起来，那么总体上就可以学习到更复杂的函数。

        边缘探测器是针对照片中很小的面积，面部探测器就会针对大一些的面积。但是主要的概念是：一般你会从比较小的细节入手，比如边缘，然后再一步步到更大更复杂的区域，比如一只眼睛或是一个鼻子；再把眼睛鼻子装在一起，组成更复杂的部分。这种从简单到复杂的金字塔状表示方法也可以应用在图像或是人脸以外的其他数据上，比如语音识别系统需要解决的就是如何可视化语音，你输入一个音频片段，神经网络的第一层可能就会先开始试着探测比较低频次的音频波形的一些特征（音频高低、音色等），然后把这些波形组合在一起，就能去探测声音的基本单元·（音位：单词的发音）；把音位组合起来就能识别音频中的单词，单词再结合就能识别词组，再到完整的句子。

        神经网络的很多隐藏层，前几层能学习到一些低层次的简单特征（比如图像单元的边缘等），等到后几层把简单特征结合起来去探测更复杂的东西（探测面部、探测单词、短语、句子等）。

        另外一个关于神经网络为什么有效的理论来源于电路理论，它和你能够用电路元件计算哪些函数有着分不开的联系。根据不同的基本逻辑门（与、或、非门）。在非正式情况下，这些函数都可以用相对较小（隐藏单元的数量相对较小）但很深的神经网络来计算。即：用含有多个隐藏层的神经网络计算，每层需要的神经元数目较少。如果只有一层隐藏层，那么这层需要大量的结点才能完成这个算法。

5  构建深度神经网络模块

        这是一个层数较少的神经网络，我们从第二层隐藏层入手。L层你有参数和；正向传播的激活函数输入是前一层的，输出是；，，并且把的值缓存。

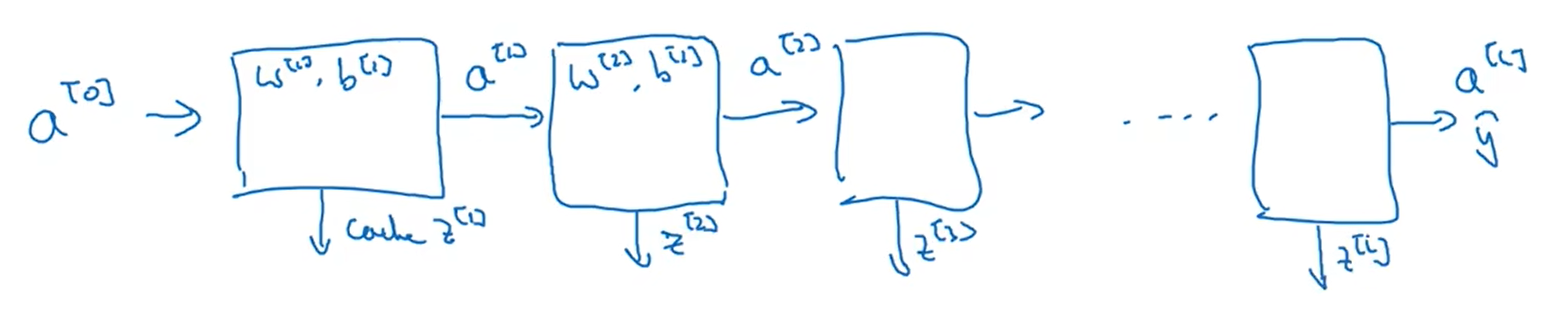
        把放入第一层并用和计算第一层的激活函数，并缓存值；之后在第二层里用到和计算出，并缓存值；根据这样一步步计算，最后计算出最终的输出，这就是正向传播的步骤。

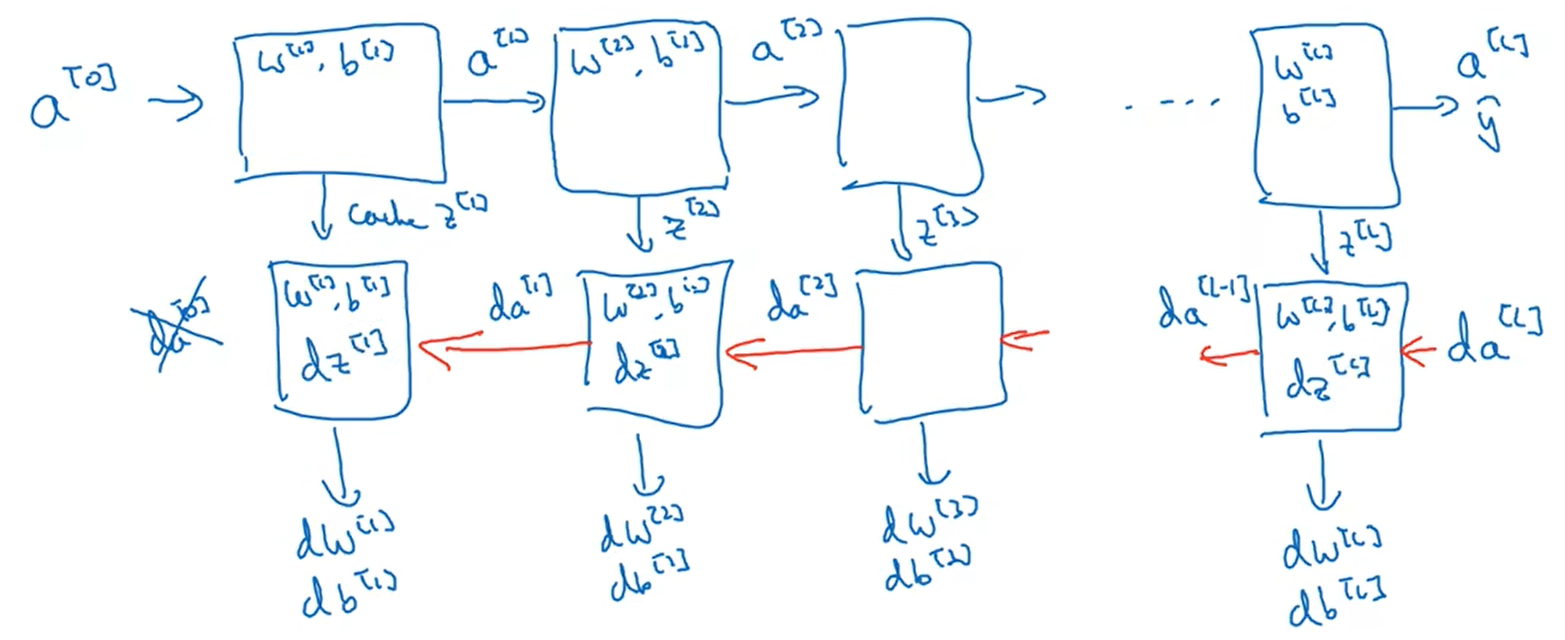
        对于反向传播的步骤而言，我们需要计算一系列的反向迭代。输入以及缓存的值，输出、和

6  参数与超参数

        想让神经网络运行地更有效，我们需要好好地设置参数和超参数。

        在神经网络中，我们常见的参数就是w和b，而在整个学习算法的模型中，还有另一些参数需要输入到学习算法中（比如学习率和梯度下降算法中的迭代次数、隐藏层数、隐藏单元数、激活函数），这些参数实际上控制了最后参数w和b值。

        实际上，深度学习有很多不同的超参数，深度学习应用领域还是很经验性的过程，你很难确定超参数的最优值应该是什么，所以通常你需要尝试不同的值，看效果的好坏，再考虑是否调整。

7  神经元和大脑

        神经网络最初的被发明动机是：编写能够模仿人类或生物大脑学习或思考的软件。尽管今天，神经网络有时也被称为人工神经网络，但是已经与我们任何一个人可能认为的大脑实际工作和学习方式大不相同。

        这是一张展示大脑中神经元外观的示意图。神经元接收来自其他神经元的电脉冲信号，并进行计算，把信息传输给其他神经元；而这个上层神经元的输出又成为下层神经元的输入，进过处理，又传输信息给其他神经元。

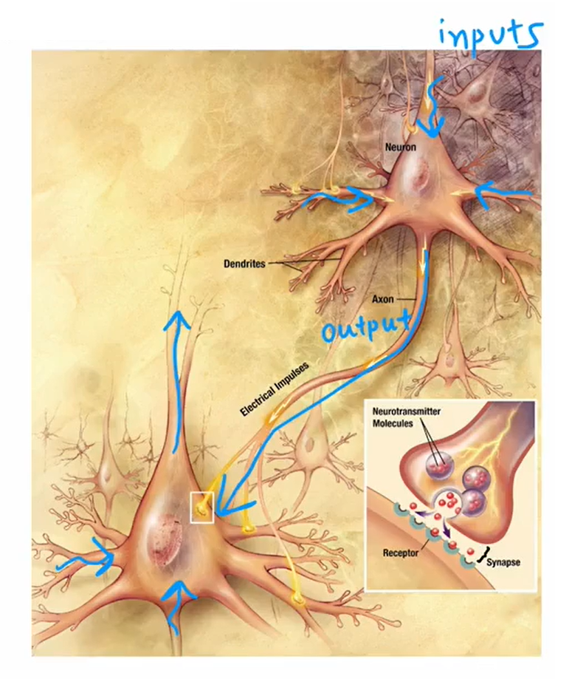
  这是一个简化的生物神经元示意图。一个神经元包含一个细胞体，神经元有不同的输入。在生物神经元中，输入线被称为树突，它会通过输出线像其他神经元发送电脉冲，输出线被称为轴突。这个神经元随后可能会发送电脉冲，成为另一个神经元的输入。

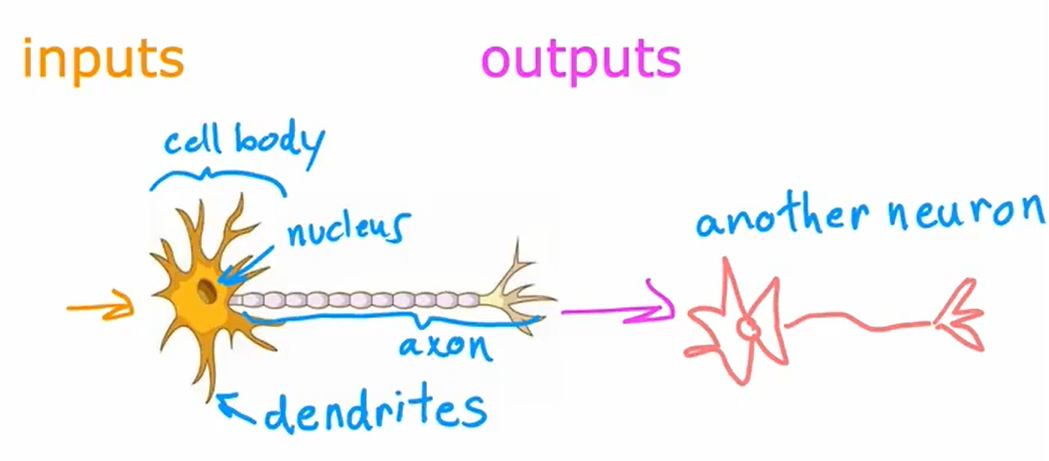
        人工神经网络使用了一个非常简化的数学模型来模拟生物神经元的功能。 下图用小圆表示神经元：

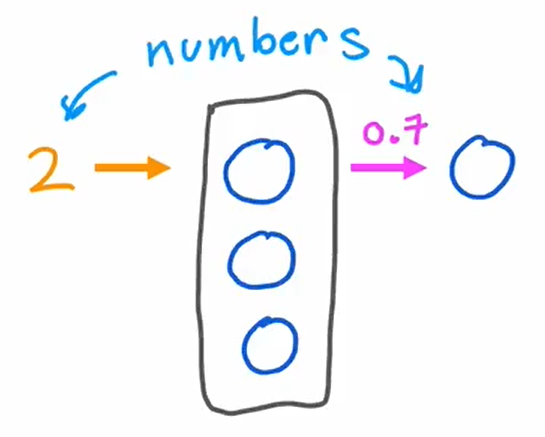
        信息输入到神经元进行计算，再经过激活函数进行处理，之后，它要么到达目的地，要么进入另一个神经元。

        当今大多数深度学习的研究几乎没有直接从神经科学中获得灵感。斯图尔特·罗素和彼得·诺维格在 他们的经典人工智能教科书 Artificial Intelligence:A Modern Approach (Russell and Norvig, 2016) 中说：虽然飞机可能受到鸟类的启发，但几个世纪以来，鸟类学并不是航空创新的主要驱动力。同样地，如今在深度学习中的灵感同样或更多地来自数学、统计学和计算机科学。