各种 dp 刷题下

6.#8518 杰瑞征途 / 洛谷 P4072 征途

题意

Pine 开始了从 $S$ 地到 $T$ 地的征途。从 $S$ 地到 $T$ 地的路可以划分成 $n$ 段，相邻两段路的分界点设有休息站。Pine 计划用 $m$ 天到达 $T$ 地。除第 $m$ 天外，每一天晚上 Pine 都必须在休息站过夜。所以，一段路必须在同一天中走完。

Pine 希望每一天走的路长度尽可能相近，所以他希望每一天走的路的长度的方差尽可能小。帮助 Pine 求出最小方差是多少。

设方差是 $v$，可以证明，$v\times m^2$ 是一个整数。为了避免精度误差，输出结果时输出 $v\times m^2$。

$1\le n\le 3000$，保证从 $S$ 到 $T$ 的总路程不超过 $3\times 10^4$，$2\le m\le n$，每段路的长度为不超过 $3\times 10^4$ 的正整数。

思路

先转化一下方差：$s^2=-\frac{{\left(\sum _{i=1}^m{x}_i\right)}^2}{m^2}+\frac{\sum _{i=1}^m{x}_i^2}{m}$。乘上 $m^2$ 就是：
$$-{\left(\sum _{i=1}^m{x}_i\right)}^2+m\left(\sum _{i=1}^m{x}_i^2\right)$$

式子左边是个定值，因此 dp 做右边。设 $f_{i,j}$ 表示第 $i$ 天走完了前 $j$ 段，每段路径和的各自平方之和的最小值，形如 $\sum _{t=1}^j{x}_t^2$。不妨设 $s_i={\sum }_{t=1}^i{a}_t$，有转移：
fi,j=min⁡{fi−1,k+(sj−sk)2}f_{i,j}=\min\{f_{i-1,k}+(s_j-s_k)^2\}fi,j​=min{fi−1,k​+(sj​−sk​)2}

初始化 $f_{1,i}=s_i^2$。

这个转移是 $O(n^2)$ 的，可以斜率优化整一整。枚举 $i,j$，设 $k1<k2$ 且 $k2$ 优于 $k1$：
$$f_{i-1,k1}+s_j^2+s_{k1}^2-2s_j{s}_{k1}>f_{i-1,k2}+s_j^2+s_{k2}^2-2s_j{s}_{k2}$$

$$\frac{f_{i-1,k1}-f_{i-1,k2}+s_{k1}^2-s_{k2}^2}{s_{k1}-s_{k2}}<2s_j$$

是 $slope<x_i$ 的形式，维护单调递增斜率，最优决策取队首。

记得对每个 $j$ 计算完之后，清空单调队列。

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define dd double
const ll N=3005;
ll n,m;
ll a[N],s[N];
ll f[N][N],q[N];
ll _2(ll x)
{return x*x;
}
double slope(ll i,ll j1,ll j2)
{return (dd)(f[i][j1]-f[i][j2]+_2(s[j1])-_2(s[j2]))/(dd)(s[j1]-s[j2]);
}
int main()
{scanf("%lld%lld",&n,&m);for(int i=1;i<=n;i++){scanf("%lld",&a[i]);s[i]=s[i-1]+a[i];}for(int i=1;i<=n;i++)f[1][i]=_2(s[i]);for(int i=2;i<=m;i++){ll hh=1,tt=0;for(int j=1;j<=n;j++){while(hh<tt&&slope(i-1,q[hh],q[hh+1])<=2*s[j])hh++;f[i][j]=f[i-1][q[hh]]+_2(s[j]-s[q[hh]]);while(hh<tt&&slope(i-1,q[tt],j)<slope(i-1,q[tt-1],q[tt]))tt--;q[++tt]=j;}}printf("%lld",m*f[m][n]-_2(s[n]));return 0;
}

7.#2576 斜率

题意

平面中有 $n$ 个点 $(x_i,y_i)$，有 $m$ 条直线，它们的斜率 $k_j$ 已经确定。对于 $m$ 条直线需要在给定的 $n$ 个点中，选出一个点 $(x,y)$，使 $kx+y$ 最大。

思路

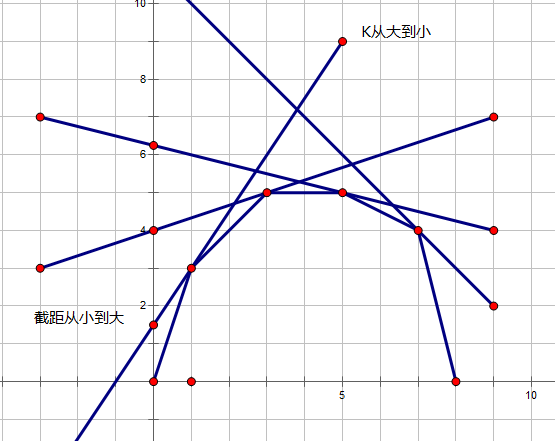
看表达式：$kx+y$——如果把 $k$ 取相反数，那么就是直线的表达式，求截距。那么就只要维护一个上凸包即可——因为题目中的式子，所以在图中的斜率正负是相反的，即维护斜率递减。

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define dd double
const ll N=1e5+9;
ll n,m;
struct point
{ll x,y;
}p[N],stk[N];
ll top;
bool cmp1(point x,point y)
{if(x.x!=y.x)return x.x<y.x;return x.y<y.y;
}
struct kk
{ll k,id;
}a[N];
bool cmp2(kk x,kk y)
{return x.k<y.k;
}
bool check(point x,point y,point z)
{return (y.y-x.y)*(z.x-y.x)<=(z.y-y.y)*(y.x-x.x);
}
ll cal(ll id,ll k)
{return k*stk[id].x+stk[id].y;
}
ll ans[N];
int main()
{scanf("%lld%lld",&n,&m);for(int i=1;i<=n;i++){ll x,y;scanf("%lld%lld",&x,&y);p[i]=(point){x,y};}for(int i=1;i<=m;i++){ll k;scanf("%lld",&k);a[i]=(kk){k,i};}sort(p+1,p+n+1,cmp1);sort(a+1,a+m+1,cmp2);stk[++top]=p[1];stk[++top]=p[2];for(int i=3;i<=n;i++){while(top>1&&check(stk[top-1],stk[top],p[i]))top--;stk[++top]=p[i];}ll pos=1;for(int i=1;i<=m;i++){while(pos<top&&cal(pos,a[i].k)<=cal(pos+1,a[i].k))pos++;ans[a[i].id]=cal(pos,a[i].k);}for(int i=1;i<=m;i++)printf("%lld\n",ans[i]); return 0;
}

8.#3074 米仓 / 洛谷 P5844 IOI2011 Ricehub

9.#6448 挖油 / SP4305 AE3A

10.#3035 过河 / 洛谷 P1052 过河

我的博客，nflsoi 7.26

11. #3716 基站选址 / 洛谷 P2605 ZJOI2010 基站选址

题意

有 $N$ 个村庄坐落在一条直线上，第 $i(i>1)$ 个村庄距离第 $1$ 个村庄的距离为 $D_i$。需要在这些村庄中建立不超过 $K$ 个通讯基站，在第 $i$ 个村庄建立基站的费用为 $C_i$。如果在距离第 $i$ 个村庄不超过 $S_i$ 的范围内建立了一个通讯基站，那么就村庄被基站覆盖了。如果第 $i$ 个村庄没有被覆盖，则需要向他们补偿，费用为 $W_i$。现在的问题是，选择基站的位置，使得总费用最小。

$K\le N$，$K\le 100$，$N\le 2\times 10^4$，$D_i\le 10^9$，$C_i\le 10^4$，$S_i\le 10^9$，$W_i\le 10^4$。

思路

设 $f_{i,j}$ 表示，在前 $i$ 个村庄建立了 $j$ 个基站，$i$ 必须建的最小费用。那么：
fi,j=min⁡j−1≤k<i{fk,j−1+costk,i}+cif_{i,j}=\min_{j-1\le k<i}\{f_{k,j-1}+cost_{k,i}\}+c_ifi,j​=j−1≤k<imin​{fk,j−1​+costk,i​}+ci​

其中 $cos{t}_{k,i}$ 表示，在 $k$ 村到 $i$ 村之间不建基站，将会产生的赔偿费用。这一题的时间瓶颈也就在计算这个 $cost$。

考虑如何让一个村产生赔偿费用：维护 $s{t}_i,e{n}_i$ 表示，能够覆盖 $i$ 的基站之中的最左站和最右站（容易二分 lower_bound 维护）。$\forall e{n}_k=i$，如果没有一个基站建在其中一个 $k$ 上，$i$ 前面就没有一个基站能够覆盖它，将会产生 $w_i$ 费用；以及前面不建和不在 $i$ 建，就会产生 $\sum w_k$ 的费用。

那么用一个 vector 存下这些 $e{n}_k=i$ 的 $k$ 村。这时回到式子，首先降维将 $j$ 省去，考虑用线段树维护 $f_k+cos{t}_{k,i}$，查询最小值并修改。

枚举基站个数 $j$ 和基站建设位置 $i$。初始时将 $j-1$ 个基站时的 $f_{\mathrm{1...}n}$ 扔上线段树；每次转移 $f_i$ 时，查询最小的 $f_k+cos{t}_{k,i}$，再加上 $c_i$；维护时，对于所有 $e{n}_k=i$，将 $1\sim s{t}_k-1$ 加上 $w_k$，表示不在 $i$ 建基站，这些 $k$ 村会产生的赔偿费用，为 $\min$ 取在不选 $i$ 的维护，增加 $cost$。

时间复杂度 $O(kn\log n)$，我的思路和实现参考了这篇和这篇题解。

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define ls u<<1
#define rs u<<1|1
const ll N=2e4+9,inf=3e14;
ll n,k;
ll d[N],c[N],s[N],w[N];
ll st[N],en[N];
ll f[N];
vector<ll>vec[N];
//不在buc(i)里的元素(<i)建基站，就覆盖不到i 
struct SegT
{struct node{ll mi;ll tag;}T[N<<2];void pushup(ll u){T[u].mi=min(T[ls].mi,T[rs].mi);}void modi(ll u,ll tg){T[u].mi+=tg;T[u].tag+=tg;}void pushdown(ll u,ll l,ll r){modi(ls,T[u].tag);modi(rs,T[u].tag);T[u].tag=0;}void build(ll u,ll l,ll r){T[u].mi=T[u].tag=0;if(l==r){T[u].mi=f[l];return;}ll mid=(l+r)>>1;build(ls,l,mid);build(rs,mid+1,r);pushup(u);}void modify(ll u,ll l,ll r,ll ql,ll qr,ll k){if(qr<l||r<ql)return;if(ql<=l&&r<=qr){T[u].mi+=k;T[u].tag+=k;return;}pushdown(u,l,r);ll mid=(l+r)>>1;if(ql<=mid)modify(ls,l,mid,ql,qr,k);if(qr>mid)modify(rs,mid+1,r,ql,qr,k);pushup(u);}ll query(ll u,ll l,ll r,ll ql,ll qr){if(qr<ql)return inf;if(ql<=l&&r<=qr)return T[u].mi;pushdown(u,l,r);ll mid=(l+r)>>1,ret=inf;if(ql<=mid)ret=min(ret,query(ls,l,mid,ql,qr));if(qr>mid)ret=min(ret,query(rs,mid+1,r,ql,qr));return ret;}
}A;
int main()
{scanf("%lld%lld",&n,&k);for(int i=2;i<=n;i++)scanf("%lld",&d[i]);for(int i=1;i<=n;i++)scanf("%lld",&c[i]);for(int i=1;i<=n;i++)scanf("%lld",&s[i]);for(int i=1;i<=n;i++)scanf("%lld",&w[i]);d[++n]=inf;w[n]=inf;for(int i=1;i<=n;i++){st[i]=lower_bound(d+1,d+n+1,d[i]-s[i])-d;en[i]=lower_bound(d+1,d+n+1,d[i]+s[i])-d;if(d[en[i]]>d[i]+s[i])en[i]--;vec[en[i]].push_back(i);}ll cur=0;for(int i=1;i<=n;i++)//初始化：只在i修基站 {f[i]=cur+c[i];for(auto x:vec[i])cur+=w[x];}ll ans=inf,sum=0;for(int i=1;i<n;i++)sum+=w[i];ans=min(ans,sum);for(int j=1;j<=k;j++)//基站个数,k实际为k+1 {A.build(1,1,n);for(int i=1;i<=n;i++){f[i]=A.query(1,1,n,1,i-1)+c[i];for(auto x:vec[i])A.modify(1,1,n,1,st[x]-1,w[x]);}ans=min(ans,f[n]);//n实际为n+1，取了f(1~n)的最小值 }printf("%lld",ans);return 0;
}

12.#10927 划分区间 / CF833B The Bakery

题意

将一个长度为 $n$ 的序列分为 $m$ 段，使得总价值最大。一段区间的价值表示为区间内不同数字的个数。

$1\le n\le 35000$，$1\le m\le 50$。

思路

设 $f_{i,j}$ 表示，前 $i$ 个数被分割 $j$ 次的最大价值。那么找一个决策点：
fi,j=max⁡k≤i{fk−1,j−1+cntk,i}f_{i,j}=\max_{k\le i}\{f_{k-1,j-1}+cnt_{k,i}\}fi,j​=k≤imax​{fk−1,j−1​+cntk,i​}

其中 $cn{t}_{l,r}$ 表示区间内不同数字的个数。如何快速取 $\max$ 和一并统计 $cn{t}_{k,i}$ 的值？其实这是一个区间最大值，考虑用线段树维护 $f_{k-1,j-1}+cn{t}_{k,i}$，那么只需要想怎么在线段树上，在加进一个 $a_i$ 时修改一段贡献了。

我们不难维护对于每个 $a_i$，它的上一个出现的位置 $pr{e}_i$，在区间 $(pr{e}_i,i]$ 中 $a_i$ 只出现一次，那么 $a_i$ 对 $(pr{e}_i,i]$ 的贡献 $+1$。在线段树上 pre[a[i]]+1,i 区间 $+1$ 即可。

枚举分割次数 $j$，根据转移式子，每次“分割”前先在线段树上初始化 $f_{i-1,j-1}$。

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define ls u<<1
#define rs u<<1|1
const ll N=4e5+9,inf=3e14;
ll n,k;
ll a[N],pre[N],pos[N];
ll f[N][52];
struct SegT
{struct node{ll ma;ll tag;}T[N<<2];void pushup(ll u){T[u].ma=max(T[ls].ma,T[rs].ma);}void modi(ll u,ll tg){T[u].ma+=tg;T[u].tag+=tg;}void pushdown(ll u,ll l,ll r){modi(ls,T[u].tag);modi(rs,T[u].tag);T[u].tag=0;}void build(ll u,ll l,ll r,ll j){T[u]={0,0};if(l==r){T[u].ma=f[l-1][j];return;}ll mid=(l+r)>>1;build(ls,l,mid,j);build(rs,mid+1,r,j);pushup(u);}void modify(ll u,ll l,ll r,ll ql,ll qr,ll k){if(qr<l||r<ql)return;if(ql<=l&&r<=qr){T[u].ma+=k;T[u].tag+=k;return;}pushdown(u,l,r);ll mid=(l+r)>>1;if(ql<=mid)modify(ls,l,mid,ql,qr,k);if(qr>mid)modify(rs,mid+1,r,ql,qr,k);pushup(u);}ll query(ll u,ll l,ll r,ll ql,ll qr){if(ql<=l&&r<=qr)return T[u].ma;pushdown(u,l,r);ll mid=(l+r)>>1,ret=-inf;if(ql<=mid)ret=max(ret,query(ls,l,mid,ql,qr));if(qr>mid)ret=max(ret,query(rs,mid+1,r,ql,qr));return ret;}
}A;
int main()
{scanf("%lld%lld",&n,&k);for(int i=1;i<=n;i++){scanf("%lld",&a[i]);pre[i]=pos[a[i]];pos[a[i]]=i;}for(int j=1;j<=k;j++){A.build(1,1,n,j-1);for(int i=1;i<=n;i++){A.modify(1,1,n,pre[i]+1,i,1);f[i][j]=A.query(1,1,n,1,i);}}printf("%lld",f[n][k]);return 0;
}

13.洛谷 P11233 CSPS2024 染色

题意

给定一个长度为 $n$ 的正整数数组 $A$，其中所有数从左至右排成一排。

你需要将 $A$ 中的每个数染成红色或蓝色之一，然后按如下方式计算最终得分：

设 $C$ 为长度为 $n$ 的整数数组，对于 $A$ 中的每个数 $A_i$（$1\le i\le n$）：

• 如果 $A_i$ 左侧没有与其同色的数，则令 $C_i=0$。
• 否则，记其左侧与其最靠近的同色数为 $A_j$，若 $A_i=A_j$，则令 $C_i=A_i$，否则令 $C_i=0$。

你的最终得分为 $C$ 中所有整数的和，即 $\sum _{i=1}^n{C}_i$。你需要最大化最终得分，请求出最终得分的最大值。

$n\le 2\times 10^5$，$a_i\le 10^6$。

思路

上一年 $O(n^2)$ 都不会写，真的很笨诶……，不过如果想到 $O(n^2)$ 感觉正解也很好想，不过当时都快急哭了没办法冷静下来。

我们不难维护数 $a_i$ 上一次出现位置 $pr{e}_{a_i}$，我们想要把 $pr{e}_{a_i}$ 和 $i$ 涂成一个颜色，然后 $(pr{e}_{a_i},i)$ 涂成另外一种颜色，再加上区间 $(pr{e}_{a_i},i)$ 全部涂成一种颜色会产生多少贡献以及 $a_i$。

设 $f_i$ 表示，以 $i$ 为结尾的序列的最大价值。我们考虑从 $f_{pr{e}_{a_i}}$ 转移过来，预处理 $g_{l,r}$ 表示区间 $[l,r]$ 全部涂成一种颜色产生总贡献，可以先考虑枚举 $[l,r]$，$O(n^2)$ 计算。

for(int i=1;i<=n;i++)
{for(int j=i+1;j<=n;j++){g[i][j]=g[i][j-1];if(a[j]==a[j-1])g[i][j]+=a[j];//区间(i,j)全部涂红产生的贡献 }
}

转移式即：
$$f_i=\max (f_{i-1},f_{pr{e}_{a_i}}+g_{pr{e}_{a_i}+1,i-1}+a_i)$$

但是带入样例检验，我们发现第 $3$ 组数据错输出 $6$，少了来自 $2$ 的贡献。这是为什么呢？我们发现，在做 $f_{pr{e}_{a_i}+1}$ 的转移时，$pr{e}_{a_i}$ 和 $pr{e}_{a_i}+1$ 两个位置染成了不同颜色，现在也如此：所以 $f_{pr{e}_{a_i}+1}$ 在当前情况是合法的，要算上：
$$f_i=\max (f_{i-1},\max (f_{pr{e}_{a_i}},f_{pr{e}_{a_i}+1})+g_{pr{e}_{a_i}+1,i-1}+a_i)$$

又因为做 $f_{pr{e}_{a_i}+1}$ 时已经和 $f_{pr{e}_{a_i}}$ 取过 $\max$ 了，于是 $\max (f_{pr{e}_{a_i}},f_{pr{e}_{a_i}+1})=f_{pr{e}_{a_i}+1}$。

现在是 $O(n^2)$ 的，瓶颈居然不在转移而在预处理 $g$——其实只要把 $g$ 转化成前缀和形式，就可以 $O(n)$ 了。

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll N=2000+9,M=1e6+9;
ll Q,n;
ll a[N];
ll pre[M],f[N],g[N][N];
void clean()
{memset(g,0,sizeof(g));memset(f,0,sizeof(f));memset(pre,0,sizeof(pre));
}
int main()
{scanf("%lld",&Q);while(Q--){scanf("%lld",&n);for(int i=1;i<=n;i++)scanf("%lld",&a[i]);for(int i=1;i<=n;i++){for(int j=i+1;j<=n;j++){g[i][j]=g[i][j-1];if(a[j]==a[j-1])g[i][j]+=a[j];//区间(i,j)全部涂红产生的贡献 }}ll ans=0;for(int i=1;i<=n;i++){f[i]=f[i-1];if(pre[a[i]])f[i]=max(f[i],max(f[pre[a[i]]],f[pre[a[i]]+1])+g[pre[a[i]]+1][i-1]+a[i]);ans=max(ans,f[i]);pre[a[i]]=i;}printf("%lld\n",ans);clean();}return 0;
}