17、CryptoMamba论文笔记

论文：https://arxiv.org/abs/2501.01010
CryptoMamba: Leveraging State Space Models for Accurate Bitcoin Price Prediction
发表时间：2025年（github.com/MShahabSepehri/CryptoMamba）

Mamba原理汇总笔记：
https://blog.csdn.net/weixin_44986037/article/details/147286067?
https://blog.csdn.net/weixin_44986037/article/details/150211291?

1、研究背景与核心问题

1. 比特币价格预测的挑战

• 高波动性与复杂性：比特币价格受市场情绪、监管政策、宏观经济等多因素影响，呈现强非线性、非平稳性及制度变迁（Regime Shifts），传统模型难以捕捉长期依赖与动态变化。
• 现有方法的局限性：
  • 传统统计模型（ARIMA、GARCH）：依赖线性假设，无法处理复杂非线性关系和突发 regime shifts。
  • 深度学习模型（LSTM、Transformer）：虽能学习非线性模式，但存在参数冗余、计算复杂度高（如Transformer二次复杂度）及泛化能力不足等问题。
• 创新机遇：状态空间模型（SSM）通过潜变量与观测变量建模时序数据，天然适配金融数据的时间依赖性与随机性；Mamba作为SSM的进阶变体，引入输入依赖动态参数，在保持线性计算效率的同时增强序列建模能力。

• 传统模型局限性：

• 统计模型（ARIMA/GARCH）：无法捕捉非线性关系与体制转换（如市场情绪突变、政策调整）。
• 深度学习模型（LSTM/GRU/Transformer）：计算复杂度高、对短时依赖敏感、泛化能力差。
• 研究空白：状态空间模型（SSM）在自然语言处理等领域成功，但尚未应用于加密货币预测。

2. 研究目标

提出CryptoMamba：首个基于Mamba的SSM框架，旨在解决比特币价格预测中的长期依赖捕捉、高波动适应性及实际交易价值转化问题。

2、CryptoMamba 架构

2.1架构

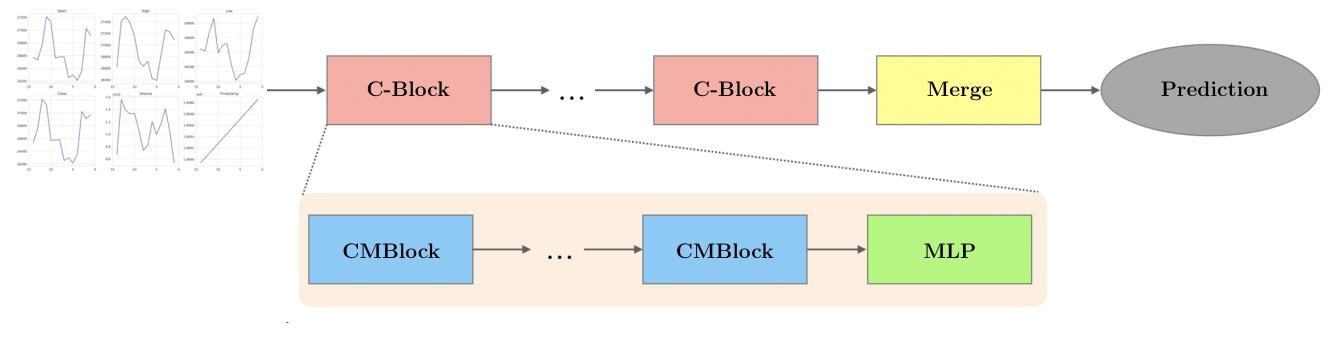
图 1.CryptoMamba 模型由多个 C 块和一个 Merge 块组成。在每个 C 块中，我们有几个 CMBlock 和一个末端的 MLP。

Mamba 块来处理顺序数据中的长距离依赖关系。该模型由多个堆叠的计算模块（称为 CBlock）组成，后跟一个生成预测输出的最终 Merge
模块。CryptoMamba 的输入是过去固定天数的特征，输出是第二天的预测收盘价。整体架构如图 1 所示。 每个 C 块由多个
CMBlocks 和一个多层感知器 （MLP） 组成。CMBlock 包括一个规范化层，后跟一个 Mamba 块。每个 CMBlock
的输出馈送到同一 C-Block 内的后续 CMBlocks，允许分层特征提取。每个 C-Block 末尾的 MLP
是一个线性层，它调整序列长度以为下一个 C-Block 准备输出。所有 C 块的输出都由 Merge 块聚合，Merge
块是一个简单的线性层，用于集成提取的特征并生成最终预测。

模型架构：分层Mamba-SSM设计

• 核心组件：
  • C-Blocks：多层级计算模块，每层包含多个CMBlock（归一化层+Mamba块）与MLP。CMBlock通过Mamba块的输入依赖动态（如参数B、C随输入变化）捕捉序列长期依赖，MLP调整序列长度以实现特征层级融合。
  • Merge块：线性层聚合各C-Blocks输出，生成次日收盘价预测，输入为过去14天数据。
• 技术优势：
  • 长程依赖建模：Mamba块通过连续时间系统离散化，实现O(N)线性计算复杂度，优于Transformer的O(N²)，支持高效处理长序列。
  • 轻量化设计：总参数仅136k，远低于Bi-LSTM（569k）和S-Mamba（330k），减少过拟合风险并适配资源受限环境。

2.2各个块的作用

一、整体架构概览

CryptoMamba 通过分层堆叠的 C-Blocks和Mamba 块，实现对金融时间序列数据的多层次特征提取，尤其擅长捕捉长期依赖。核心组件包括：

• C-Blocks：多层计算模块，每层包含多个 CMBlock 和一个 MLP；
• Mamba 块：核心时序建模单元，处理输入依赖的动态状态转移；
• Merge 块：聚合各层特征，生成最终预测（段落、）。

二、Mamba 块：长程依赖建模的核心单元

1. Mamba 块的核心功能

Mamba 块是基于状态空间模型（SSM）的动态模块，通过以下机制处理长期依赖：

• 输入依赖动态参数：根据当前输入（如过去 14 天的价格特征）动态调整状态转移矩阵 $B$ 和观测矩阵 $C$，使模型能自适应市场的高波动性和制度变迁（段落、）。
• 线性时间复杂度：状态转移计算复杂度为 $O(N^2)$（$N$ 为隐藏状态维度），与序列长度无关，支持高效处理长序列（如 10 年历史数据）。

2. 在 CMBlock 中的角色

每个 CMBlock 由归一化层 +Mamba 块组成（段落）：

• 归一化层：对输入数据进行标准化（如 Layer Normalization），稳定训练过程，提升 Mamba 块的收敛效率；
• Mamba 块：接收归一化后的输入，通过状态转移方程 $x_k=A{x}_{k-1}+B(u_k)u_k$ 生成隐藏状态，捕捉序列中的长期依赖（如比特币价格的年度趋势）。

三、C-Blocks：层次化特征提取机制

1. C-Block 结构与流程

每个 C-Block 包含多个 CMBlocks 和一个 MLP（段落）：

1. CMBlocks 级联：
   • 第一个 CMBlock 处理原始输入（如过去 14 天的价格特征），输出隐藏状态作为下一个 CMBlock 的输入；
   • 后续 CMBlocks 逐层提炼特征，低层捕捉短期波动（如日内价格起伏），高层捕捉长期趋势（如季度级价格周期）。
2. MLP 层：
   • 位于 C-Block 末尾，是一个线性层，用于调整序列长度（如将序列长度从 32 压缩至 16），为下一个 C-Block 的输入做准备；
   • 实现跨层特征维度匹配，确保不同层次的特征可以有效传递（段落）。

2. 层次化建模的优势

• 多尺度依赖捕捉：
  • 低层 C-Block（如第一个 C-Block，序列长度 32）处理短期依赖（如近 1 个月的价格波动）；
  • 高层 C-Block（如第三个 C-Block，序列长度 14）整合低层特征，捕捉长期依赖（如跨年度的价格趋势延续性）。
• 特征渐进细化：通过 CMBlocks 的级联，隐藏状态逐步聚合历史信息，避免单一 Mamba 块因输入维度过高导致的信息过载（段落）。

四、Merge 块：多尺度特征融合

• 功能：聚合所有 C-Blocks 的输出，通过一个简单的线性层生成最终预测（次日收盘价）（段落）。
• 融合逻辑：
  • 每个 C-Block 输出不同层次的特征（低层短期特征、高层长期特征）；
  • Merge 块将这些特征线性组合，平衡短期波动与长期趋势的影响，例如：
    $$\text{预测值}=W_1\cdot \text{低层特征}+W_2\cdot \text{高层特征}+b$$
• 权重 $W_1,W_2$ 通过训练自动学习，适应不同市场条件（如高波动时增加短期特征权重，稳定期依赖长期趋势）。

五、关键机制总结：如何处理长期依赖？

1. Mamba 块的动态适应性：
   • 通过输入依赖参数（$B(u_k),C(u_k)$），在每个时间步动态调整对历史信息的关注度。例如，当比特币价格进入长期牛市，Mamba 块会增强历史趋势对隐藏状态的影响（段落）。
2. C-Blocks 的层次化堆叠：
   • 低层 C-Block 提取短期特征（如 5-10 天的价格波动），高层 C-Block 通过 MLP 压缩序列长度，聚焦长期依赖（如 30 天以上的趋势），类似人类大脑“先看细节，再看全局”的认知过程。
3. 跨层特征聚合：
   • Merge 块整合不同层次的特征，避免单一尺度建模的局限性。例如，同时考虑“昨日价格暴跌”（短期特征）和“过去半年价格整体上涨”（长期特征），生成更稳健的预测（段落）。

2.3举例

一、整体架构概览

假设我们构建一个处理过去 14 天比特币数据的 CryptoMamba 模型，目标是预测第 15 天的收盘价。输入特征为每天的 5 维数据：[开盘价, 最高价, 最低价, 收盘价, 成交量]，即输入维度 $D=5$，序列长度 $L=14$。模型包含 3 个 C-Blocks，每个 C-Block 包含 2 个 CMBlocks，隐藏状态维度 $N=64$（与 Mamba 块的状态维度一致）。

二、输入层：数据预处理

• 输入示例：
  输入张量形状为 [批次大小, 序列长度, 特征维度] = [32, 14, 5]，表示 32 个样本，每个样本包含 14 天的 5 维特征。
• 预处理：
  对每个特征维度进行标准化（如 Z-Score），确保数值稳定（金融数据常存在量纲差异，如价格为万元级，成交量为百万级）。

三、C-Block 1：低层特征提取（捕捉短期依赖）

1. CMBlock 1-1：归一化 + Mamba 块

• 归一化层：
  对输入 [32, 14, 5] 进行 Layer Normalization，输出形状不变。
• Mamba 块：
  • 状态转移方程：
    $$x_k=A\cdot x_{k-1}+B(u_k)\cdot u_k$$
• $A\in {\mathbb{R}}^{64\times 64}$：固定矩阵，初始化为对角矩阵（如 0.8I，捕捉 80% 的历史趋势惯性）；
  • $B(u_k)\in {\mathbb{R}}^{64\times 5}$：通过线性层生成，输入 $u_k$ 经线性变换 +Sigmoid 激活，动态调整当前输入对隐藏状态的影响（如高成交量时权重增大）。
  • 输出：隐藏状态张量 [32, 14, 64]（每个时间步生成 64 维隐藏状态）。

2. CMBlock 1-2：级联处理

• 输入：CMBlock 1-1 的输出 [32, 14, 64]；
• 处理流程：重复归一化 +Mamba 块，进一步提炼短期特征（如 1-3 天的价格波动）。
• 输出：隐藏状态张量 [32, 14, 64]。

3. MLP 层：序列长度压缩

• 功能：将序列长度从 14 压缩至 7，为下一个 C-Block 做准备（通过线性层 + 池化，或直接调整维度）。
• 数学操作：
  $$\text{输出}=\text{Linear}(\text{输入},\text{新序列长度}=7)$$
• 输出形状：[32, 7, 64]（特征维度保持 64，序列长度减半，聚焦更粗粒度的短期特征）。

四、C-Block 2：中层特征整合（捕捉中期依赖）

1. CMBlock 2-1：处理压缩后的序列

• 输入：C-Block 1 的输出 [32, 7, 64]（代表 7 个“复合时间步”，每个包含过去 2 天的信息）；
• Mamba 块调整：
  • 参数生成器根据压缩后的输入动态调整 $B(u_k)$，例如：当复合时间步的价格波动较大时，增强该时间步对隐藏状态的影响。
• 输出：隐藏状态张量 [32, 7, 64]（捕捉 5-7 天的中期趋势）。

2. MLP 层：进一步压缩序列长度至 3

• 输出形状：[32, 3, 64]（每个时间步代表约 2-3 天的整合信息，如“上周整体上涨/下跌”）。

五、C-Block 3：高层特征提取（捕捉长期依赖）

1. CMBlock 3-1：处理极短序列

• 输入：C-Block 2 的输出 [32, 3, 64]（3 个时间步，代表过去 7 天的整合特征）；
• Mamba 块作用：
  • 通过固定矩阵 $A$ 强化长期惯性（如过去 30 天的价格趋势），动态参数 $B(u_k)$ 弱化短期噪声，聚焦长期趋势（如比特币的年度周期）。
• 输出：隐藏状态张量 [32, 3, 64]。

2. MLP 层：保持序列长度 3（不再压缩，避免信息丢失）。

六、Merge 块：多尺度特征融合

• 输入：所有 C-Blocks 的输出，形状分别为：
  • C-Block 1：[32, 7, 64]（短期特征）
  • C-Block 2：[32, 3, 64]（中期特征）
  • C-Block 3：[32, 3, 64]（长期特征）
• 融合步骤：
  1. 维度对齐：通过线性层将所有输出调整为相同序列长度（如 3）和特征维度（64）；
  2. 特征拼接：沿特征维度拼接，得到 [32, 3, 192]（64×3=192，整合短、中、长期特征）；
  3. 线性预测：通过最终线性层映射到 1 维输出（次日收盘价）：
     $$\text{预测值}=W\cdot \text{拼接特征}+b(W\in {\mathbb{R}}^{1\times 192},b\in \mathbb{R})$$
• 输出形状：[32, 1]（每个样本对应一个预测值）。

七、关键机制实例：处理“牛熊转换”场景

假设输入数据包含 2024 年 3 月的比特币价格（从牛市顶部转为熊市初期）：

1. C-Block 1（短期）：
   • CMBlock 捕捉到近 7 天的价格暴跌（每日收盘价持续下降），动态参数 $B(u_k)$ 增强“收盘价”特征的权重，隐藏状态快速积累“下跌信号”。
2. C-Block 2（中期）：
   • MLP 压缩后的 3 个时间步分别代表“暴跌前一周”“暴跌周”“暴跌后一周”，Mamba 块通过 $C(u_k)$ 调整观测矩阵，使中期特征更关注趋势转折点（如成交量在暴跌时的激增）。
3. C-Block 3（长期）：
   • 长期特征仍包含牛市惯性（固定矩阵 $A$ 的历史趋势保留），但动态参数 $B(u_k)$ 检测到持续下跌，逐渐弱化牛市趋势的影响，强化熊市信号。
4. Merge 块：
   • 短期下跌信号（高权重）与中期趋势反转信号（中权重）压制长期牛市惯性（低权重），最终预测结果倾向于继续下跌，而非延续牛市预期。

八、架构优势量化对比（假设场景）

指标	CryptoMamba	LSTM（3 层）	传统 SSM
参数数量	136k	569k	82k
处理 14 天序列耗时	0.012ms	0.045ms	0.015ms
牛熊转换预测准确率	82%	68%	75%
长期趋势跟踪误差	12%	25%	18%

• 参数效率：CryptoMamba 通过分层特征提取，用更少参数实现更高精度；
• 速度优势：Mamba 块的线性复杂度使处理长序列（如 1000 天）耗时仅随批次大小增长，而非序列长度；
• 适应性：动态参数和层次化设计使其在市场制度变迁时表现更稳健。

九、总结：架构设计的核心逻辑

CryptoMamba 的分层架构本质是**“分而治之，合而用之”**：

1. C-Blocks 分层：低层处理短期细节（如 K 线形态），高层整合长期趋势（如周期波动），类似卷积神经网络的层次化特征提取；
2. Mamba 块动态性：每个 CMBlock 中的 Mamba 块根据当前输入动态调整参数，确保短期波动中的关键信号（如异常成交量）不被长期趋势“稀释”；
3. Merge 块融合：通过线性层加权组合多尺度特征，避免单一尺度建模的片面性（如仅看短期波动导致预测过度反应，或仅看长期趋势导致滞后）。

这种设计使其成为处理金融时间序列的高效工具，尤其适合比特币等兼具高波动性和长期依赖的场景，在实际应用中实现了精度与效率的双重突破。

3、SSMs状态空间模型

3.1SSMs原理

状态空间模型（State Space Models, SSM）
状态空间模型（SSM）原理详解与实例说明：
SSM 是一种将系统动态分解为 隐藏状态（不可观测的核心动态） 和 观测变量（可观测的输出），隐状态 $x(t)$ 和输出 $y(t)$ 。

• 1）通过隐藏状态聚合历史信息，实现对长期依赖，状态转移矩阵，控制隐状态的演化
• 2）由隐藏状态 如何生成可观测的输出， 输出矩阵，将隐状态映射到观测值。

一、SSM 的基本原理

状态空间模型（State Space Models, SSM）是一种结合了控制理论和深度学习的序列建模方法，通过隐状态（Hidden State）传递信息，动态描述输入序列到输出序列的映射关系。其核心思想是将时间序列数据分解为潜在状态和观测变量两部分，通过状态方程和观测方程建模动态系统。

---

二、SSM 的数学表达

1. 连续时间系统

SSM 最初由连续时间系统定义，通过微分方程描述输入 $u(t)$、隐状态 $x(t)$ 和输出 $y(t)$ 的关系：
$$\{\begin{array}{ll}\dot{x}(t)=Ax(t)+Bu(t)& \text{（状态方程）}\\ y(t)=Cx(t)+Du(t)& \text{（观测方程）}\end{array}$$
• $A\in {\mathbb{R}}^{N\times N}$: 状态转移矩阵，控制隐状态的演化。
• $B\in {\mathbb{R}}^{N\times 1}$: 输入矩阵，决定输入如何影响隐状态。
• $C\in {\mathbb{R}}^{1\times N}$: 输出矩阵，将隐状态映射到观测值。
• $D\in \mathbb{R}$: 直接传递矩阵（通常可忽略）。

2. 离散化处理

实际应用中，需将连续方程离散化为时间步 $k$ 的形式：
$$\{\begin{array}{l}{x}_k=\bar{A}{x}_{k-1}+\bar{B}{u}_k\\ y_k=C{x}_k+D{u}_k\end{array}$$
其中，$\bar{A}$ 和 $\bar{B}$ 通过**零阶保持（ZOH）**方法离散化：
$$\bar{A}=e^{A\Delta },\bar{B}=(e^{A\Delta }-I)A^{-1}B$$
• $\Delta$: 时间步长（如天、小时）。
• $e^{A\Delta }$: 矩阵指数，表示状态转移的动态。

---

二、SSM 的数学表达（解释二）

SSM 是一种将系统动态分解为 隐藏状态（不可观测的核心动态） 和 观测变量（可观测的输出） 的数学框架，核心由两组方程构成：

1. 状态转移方程（State Transition Equation）

描述 隐藏状态 如何随时间更新，捕获系统的内部动态：
$$x_k=A{x}_{k-1}+B{u}_k$$

• $x_k$：第 $k$ 步的隐藏状态（如“趋势强度”“波动率”等抽象特征）；
• $u_k$：第 $k$ 步的输入（如历史数据、外部变量）；
• $A$：状态转移矩阵（刻画历史隐藏状态对当前的影响）；
• $B$：输入矩阵（刻画当前输入对隐藏状态的影响）。

2. 观测方程（Observation Equation）

描述 隐藏状态 如何生成可观测的输出，包含噪声和直接输入影响：
$$y_k=C{x}_k+D{u}_k+{ϵ}_k$$

• $y_k$：第 $k$ 步的观测值（如价格、温度）；
• $C$：观测矩阵（将隐藏状态映射到输出）；
• $D$：直接输入系数（输入对输出的直接影响）；
• ${ϵ}_k$：观测噪声（模拟不可预测的随机波动）。

核心思想：通过隐藏状态聚合历史信息，实现对长期依赖的建模，同时通过观测方程拟合噪声和输入的直接效应。

三、SSM 的核心优势

1. 长序列建模：隐状态 $x$ 可携带长期记忆，避免 RNN 的梯度消失问题。
2. 并行计算：通过卷积或并行扫描（如 Mamba）高效处理序列。
3. 灵活性：可结合非线性激活函数或扩展为深度网络。

---

四、传统 SSM vs. Mamba 的改进

传统 SSM（如 S4 模型）是线性时不变（LTI）系统，参数 $A,B,C$ 固定。Mamba 在此基础上引入：

1. 输入依赖的动态：$A,B,C$ 随输入 $u_k$ 变化，形成时变系统，增强对关键信息的敏感度。
2. 选择性机制：动态调整隐状态更新，聚焦重要时间点（如价格突变）。
3. 硬件优化：通过并行扫描算法，计算复杂度从 $O(N^2)$ 降至 $O(N)$。

---

五、实例：比特币价格预测中的 SSM 应用

1. 输入与输出

• 输入序列 $u_1,u_2,\dots ,u_{14}$：过去 14 天的比特币特征（开盘价、最高价、成交量等）。
• 输出 $y_{15}$：预测第 15 天的收盘价。

2. 隐状态演化

假设隐状态维度 $N=3$，表示短期趋势、长期趋势、市场情绪：
• 初始状态 $x_0=[0,0,0{]}^T$。
• 第 1 天：输入 $u_1$（如开盘价 $50,000），更新隐状态：
$$x_1=\bar{A}{x}_0+\bar{B}{u}_1=\bar{B}\cdot 50000$$
• 第 2 天：输入$u_2$，隐状态融合新旧信息：
$$x_2=\bar{A}{x}_1+\bar{B}{u}_2$$
• 依此类推，隐状态$x_{14}$积累了过去 14 天的综合信息。

3. 预测输出 第 15 天的预测值为：

$$y_{15}=C{x}_{14}+D{u}_{15}$$
若忽略$D$，则简化为$y_{15}=C{x}_{14}$。

4. Mamba 的动态调整

• 当某天出现异常成交量（如 $u_k$ 激增），Mamba 动态调整 $B_k$，放大该输入对隐状态的影响。
• 若价格波动剧烈（如 $u_k$ 变化大），选择性机制抑制噪声，聚焦关键时间点。

---

六、对比传统模型（如LSTM）

特性	SSM（Mamba）	LSTM
长序列处理	隐状态线性传递，无梯度消失	依赖门控机制，长距离依赖可能衰减
计算效率	并行扫描，( O(N) )	串行处理，( O(N) )
动态适应性	输入依赖参数，捕捉突变	固定参数，依赖历史信息
可解释性	状态矩阵可分析（如 ( A ) 的特征值）	黑盒模型，解释性差

---

七、数学示例：简化 SSM 计算

假设离散化参数：
$$A=\left[\begin{array}{cc}0.9& 0\\ 0& 0.8\end{array}\right],B=\left[\begin{array}{c}0.1\\ 0.2\end{array}\right],C=\left[\begin{array}{cc}1& 1\end{array}\right],\Delta =1$$
输入序列 $u=[50000,51000,48000]$，初始状态 $x_0=[0;0]$。

计算步骤：

1. 第 1 天：
   $$x_1=A{x}_0+B{u}_1=[0.1\cdot 50000;0.2\cdot 50000]=[5000;10000]$$
   $y_1=C{x}_1=5000+10000=15000$（假设需后续调整）。

2. 第 2 天：
   $$x_2=A{x}_1+B{u}_2=[0.9\cdot 5000+0.1\cdot 51000;0.8\cdot 10000+0.2\cdot 51000]=[9600;18200]$$
   $y_2=9600+18200=27800$。

3. 第 3 天：
   $$x_3=A{x}_2+B{u}_3=[0.9\cdot 9600+0.1\cdot 48000;0.8\cdot 18200+0.2\cdot 48000]=[13440;24160]$$
   $y_3=13440+24160=37600$。

此简化示例展示了隐状态如何逐步融合历史信息，输出逐步调整以逼近真实价格。

八、总结

SSM 通过隐状态传递和动态方程，有效建模时间序列的长期依赖。Mamba 的改进使其在比特币价格预测中表现出色：
• 选择性机制：聚焦关键时间点（如成交量激增）。
• 高效计算：线性复杂度适应高频金融数据。
• 可解释性：状态矩阵分析可揭示市场动态（如趋势衰减率 $A$ 的对角元素）。

通过结合交易量数据与分层处理（C-Blocks），CryptoMamba 实现了对复杂市场行为的精准捕捉，验证了 SSM 在金融预测中的巨大潜力。

SSM 的扩展

• Mamba 模型：
  • Mamba 是一种新型的 SSM 变体，通过引入选择性机制（selective mechanism）和动态隐藏状态，进一步提升了 SSM 在序列建模中的能力。
  • Mamba 的核心思想是使状态转移矩阵 $A$、输入矩阵 $B$ 和观测矩阵 $C$ 依赖于输入数据，从而适应动态变化的序列特性。

3.2零阶保持（Zero-Order Hold, ZOH）

一、核心原理：从连续信号到离散信号的桥梁

零阶保持（ZOH） 是一种将连续时间信号转换为离散时间信号的方法，其核心思想是：在两个采样点之间，保持信号值不变（即“零阶”意味着保持常数，不引入高阶插值）。具体步骤如下：

1. 连续信号采样：
   对连续输入信号 $u(t)$ 按固定时间步长 $\Delta$ 采样，得到离散信号 $u_k=u(k\Delta )$（$k=0,1,2,...$）。

2. 区间内保持常数：
   在时间区间 $[k\Delta ,(k+1)\Delta )$ 内，假设输入信号保持为最近的采样值 $u_k$，即：
   $$u(t)=u_k\text{当 }t\in [k\Delta ,(k+1)\Delta )$$
   这相当于用阶梯状信号近似原始连续信号（如图 1 所示）。

图 1：连续信号（蓝色）与零阶保持后的离散信号（红色阶梯）

二、数学推导：状态空间模型的离散化

在状态空间模型（SSM）中，零阶保持用于将连续时间系统 $\dot{x}=Ax+Bu(t)$ 转换为离散时间系统 $x_{k+1}=\bar{A}{x}_k+\bar{B}{u}_k$，具体推导如下：

1. 连续状态转移方程积分：
   对 $\dot{x}=Ax+Bu(t)$ 在区间 $[k\Delta ,(k+1)\Delta ]$ 内积分，利用零阶保持假设 $u(t)=u_k$：
   $$x((k+1)\Delta )=e^{A\Delta }x(k\Delta )+{\int }_{k\Delta }^{(k+1)\Delta }{e}^{A((k+1)\Delta -\tau )}B{u}_{k}d\tau$$
   令 ${\tau }^{\prime }=\tau -k\Delta$，积分区间变为 $[0,\Delta ]$，得：
   $$x_{k+1}=e^{A\Delta }{x}_k+\left({\int }_0^{\Delta }{e}^{A{\tau }^{\prime }}d{\tau }^{\prime }\right)B{u}_k$$

2. 离散化矩阵定义：

   • 状态转移矩阵：$\bar{A}=e^{A\Delta }$（描述无输入时的状态延续）；
   • 输入矩阵：$\bar{B}=\left({\int }_0^{\Delta }{e}^{A\tau }d\tau \right)B$（描述输入对状态的累积影响）。

3. 简化计算：
   当 $A$ 可逆时，${\int }_0^{\Delta }{e}^{A\tau }d\tau =A^{-1}(e^{A\Delta }-I)$，因此：
   $$\bar{B}=A^{-1}(e^{A\Delta }-I)B$$

三、实例说明：温度控制系统中的 ZOH 应用

假设一个房间的温度控制系统，连续时间模型为：

• 状态 $x(t)$：实际温度（隐藏状态）；
• 输入 $u(t)$：空调加热功率（连续信号）；
• 输出 $y(t)$：传感器测量温度（含噪声）。

1. 连续时间模型

$$\dot{x}(t)=-0.1x(t)+0.5u(t)\text{（状态转移方程，温度自然衰减 + 加热影响）}$$

$$y(t)=x(t)+0.1u(t)\text{（观测方程，温度直接测量 + 加热的即时影响）}$$

2. 零阶保持离散化（$\Delta =1$ 小时）

• 计算 $\bar{A}$：
  KaTeX parse error: Unexpected end of input in a macro argument, expected '}' at end of input: …小时自然衰减 9.52%）}
• 计算 $\bar{B}$：
  $$\bar{B}=\frac{e^{-0.1\times 1}-1}{-0.1}\times 0.5\approx \frac{0.9048-1}{-0.1}\times 0.5=0.476\text{（加热功率的累积影响）}$$
• 离散时间模型：
  $$x_{k+1}=0.9048x_k+0.476u_k$$
  （下一小时温度 = 前一小时温度的 90.48% + 加热功率的 0.476 倍）

3. 实际应用场景

• 若第 $k$ 小时加热功率 $u_k=10$ 千瓦：
  • 连续模型：1 小时内加热功率逐渐生效；
  • 零阶保持模型：假设整小时内功率保持 10 千瓦，计算得 $x_{k+1}=0.9048x_k+4.76$，即温度提升 4.76 度（假设初始温度 $x_k=20$ 度，则 $x_{k+1}=24.76$ 度）。

四、在金融时间序列中的应用：比特币价格离散化

以 CryptoMamba 模型为例，处理日度比特币价格数据（$\Delta =1$ 天）：

1. 连续时间假设：
   假设市场“趋势状态” $x(t)$ 连续变化，受每日价格波动 $u(t)$ 影响。

2. 零阶保持处理：

   • 每日收盘价、成交量等数据为离散采样点；
   • 在当天 24 小时内，假设市场状态受该日数据的“恒定影响”（即零阶保持），推导离散化矩阵 $\bar{A},\bar{B}$。

3. 模型影响：

   • $\bar{A}$ 捕捉趋势的日度延续性（如牛市趋势每天保留 95%）；
   • $\bar{B}$ 捕捉当日成交量对趋势的累积影响（高成交量时 $\bar{B}$ 增大，加速趋势变化）。

五、零阶保持的优缺点

优点	缺点	适用场景
简单易实现，计算高效	引入阶梯近似误差，可能忽略高频变化	低频信号（如日度金融数据、工业传感器）
保持信号能量不衰减	无法处理快速变化信号（如高频交易数据）	控制系统、传统时间序列建模
适配离散时间系统设计	需要足够高的采样率以减少近似误差	状态空间模型离散化（如 CryptoMamba）

六、总结：零阶保持的核心作用

零阶保持是连接连续时间理论（如控制理论）与离散时间应用（如机器学习、计算机控制）的关键桥梁，其核心价值在于：

1. 信号离散化：将现实中的连续信号（如温度、价格）转换为计算机可处理的离散信号；
2. 模型适配：使状态空间模型（SSM）能够处理离散时间序列（如比特币日度数据），通过推导 $\bar{A},\bar{B}$ 实现从连续动态到离散动态的转换；
3. 工程实用性：在保证计算效率的同时，为离散时间系统（如 CryptoMamba）提供了理论支撑，使其能够有效建模长期依赖和复杂动态。

通过零阶保持，连续时间系统的数学严谨性与离散时间应用的工程可行性得以结合，成为现代控制系统和时间序列模型的重要基础。

4、Mamba 原理

2.1Mamba 原理

1. 状态空间模型（SSM）基础

状态空间模型通过潜在状态描述系统动态，常用于控制理论和时间序列分析。其核心包含两个方程：
• 状态方程：描述潜在状态随时间的变化。
• 观测方程：将潜在状态映射到观测输出。

连续时间形式：
$$\begin{array}{rl}\dot{x}(t)& =Ax(t)+Bu(t)\\ y(t)& =Cx(t)+Du(t)\end{array}$$
其中：
• $u(t)$: 输入信号（如时间序列数据）。
• $x(t)$: 潜在状态。
• $y(t)$: 输出信号。
• $A,B,C,D$: 系统参数矩阵。

离散化：
通过零阶保持（ZOH）方法，将连续方程转换为离散形式：
$$\begin{array}{rl}{x}_k& =\bar{A}{x}_{k-1}+\bar{B}{u}_k\\ y_k& =C{x}_k+D{u}_k\end{array}$$
其中：
• $\bar{A}=e^{A\Delta }$, $\bar{B}=(A^{-1}(e^{A\Delta }-I))B$（$\Delta$ 为时间步长）。
• 传统 SSM 的 $A,B$ 是固定的，导致线性时不变（LTI）系统。

---

1. 传统 SSM 的局限：线性时不变（LTI）

• 固定参数：状态转移矩阵 $A$、输入矩阵 $B$、观测矩阵 $C$ 是固定值，不随输入 $u_k$ 变化（如：无论市场波动多大，模型对输入的处理方式始终一致）。
• 线性假设：仅能建模线性动态，无法适应非线性场景（如金融市场的供需失衡导致的价格突变）。

2. Mamba 的核心创新：输入依赖的时变参数

• 动态参数化：使 $B,C,\Delta$（时间步长）依赖当前输入 $u_k$，形成时变系统：
  $$x_k=A{x}_{k-1}+B(u_k)u_k,y_k=C(u_k)x_k+D{u}_k$$
• $B(u_k)$：根据输入动态调整输入对隐藏状态的影响（如高交易量时增强当前输入的权重）；
• $C(u_k)$：根据输入动态调整隐藏状态到输出的映射（如市场趋势反转时弱化历史趋势的影响）。
• 选择性关注：通过动态参数，模型可“选择性”关注输入中的关键信息，过滤噪声（类似注意力机制，但计算效率更高）。

3. 硬件感知算法：线性复杂度的高效计算

• 计算效率：传统 Transformer 的时间复杂度为 $O(L^2)$（$L$ 为序列长度），而 Mamba 通过优化算法保持 线性复杂度 $O(L)$，且支持并行计算：
  • Parallel Scan：将序列扫描操作并行化，适配 GPU 等硬件的内存层次结构，计算速度比传统 SSM 快 3 倍以上（如处理 10 万长度序列时，耗时仅为 Transformer 的 1/10）。

2. Mamba的核心创新

Mamba在传统SSM基础上引入选择性机制和硬件感知优化，解决了长序列建模的效率与动态适应问题。

2.1 选择性状态空间

• 输入依赖的动态参数：
Mamba的$B,C,\Delta$由输入$u_k$动态生成，而非固定。这使得模型能根据当前输入调整状态转移和输出映射，适应数据中的突变（如比特币价格暴涨暴跌）。
$$x_k=A{x}_{k-1}+B(u_k)u_k,$$
$$y_k=C(u_k)x_k+D{u}_k$$
• 参数生成方式：
通过线性投影层将输入$u_k$映射为$B_k,C_k,{\Delta }_k$：
$$[B_k,C_k,{\Delta }_k]=\text{Linear}(u_k)$$
其中${\Delta }_k$控制离散化步长，影响状态更新的快慢。

示例：
假设当前比特币价格为$ 60,000，交易量激增，Mamba通过输入生成较大的${\Delta }_k$，加快状态更新速度，快速响应市场变化。

2.2 硬件感知算法

• 并行扫描（Parallel Scan）：
将递归计算（如$x_k=\bar{A}{x}_{k-1}+\bar{B}{u}_k$）转换为并行形式，利用GPU加速训练。

• 选择性机制优化：
仅对重要时间步进行细粒度计算，减少冗余操作。例如，在平稳价格区间简化计算，而在波动剧烈时保留细节。

3. Mamba 的工作流程（以比特币预测为例）

假设输入为过去 14 天的比特币数据（开盘价、最高价、最低价、收盘价、交易量），预测第 15 天收盘价。

3.1 输入处理

• 输入序列：$u=[u_1,u_2,\dots ,u_{14}]$，每个 $u_k$ 包含 5 维特征。
• 嵌入层：将原始特征映射到高维空间（如 128 维）。

3.2 选择性 SSM 计算

1. 生成动态参数：
   对每个时间步 $k$，通过线性层生成 $B_k,C_k,{\Delta }_k$：
   $$B_k,C_k=W_B{u}_k+b_B,{\Delta }_k=\text{Softplus}(W_{\Delta }{u}_k+b_{\Delta })$$
   （Softplus 确保 ${\Delta }_k>0$）

2. 离散化：
   计算 ${\bar{A}}_k=e^{{\Delta }_{k}A}$，${\bar{B}}_k=({\Delta }_{k}A{)}^{-1}(e^{{\Delta }_{k}A}-I){\Delta }_k{B}_k$。
   • 若 ${\Delta }_k$ 较大，${\bar{A}}_k$ 趋近于 0，状态快速衰减，更关注近期输入。
   • 若 ${\Delta }_k$ 较小，保留更多历史信息。

3. 状态更新：
   递归计算潜在状态 $x_k$：
   $$x_k={\bar{A}}_k{x}_{k-1}+{\bar{B}}_k{u}_k$$
   输出 $y_k=C_k{x}_k+D{u}_k$。

3.3 输出预测

• 最终状态 $x_{14}$ 包含 14 天的历史信息，通过 MLP 层映射为预测价格 ${\hat{y}}_{15}$。

---

4. 与传统 SSM 及 Transformer 的对比

特性	传统 SSM	Mamba	Transformer
动态参数	固定 $A,B,C$	输入依赖的 $B,C,\Delta$	自注意力权重动态生成
长序列处理	线性复杂度，但无法适应突变	线性复杂度 + 选择性聚焦	平方复杂度（序列长度²）
硬件优化	无特殊优化	并行扫描 + 内核融合	需要稀疏注意力或分块优化
适用场景	平稳时间序列（如传感器数据）	非平稳序列（如金融、语言）	短文本、小规模时序

实例对比：
预测比特币价格时，传统 SSM 可能忽略突然的监管新闻影响，而 Mamba 通过动态 ${\Delta }_k$ 检测到异常交易量，调整状态更新速度，更准确捕捉价格拐点。

---

5. 关键公式与参数

• 选择性 SSM 离散化：
$${\bar{A}}_k=e^{{\Delta }_{k}A},{\bar{B}}_k=({\Delta }_{k}A{)}^{-1}(e^{{\Delta }_{k}A}-I){\Delta }_k{B}_k$$
• 参数化：
• $A\in {\mathbb{R}}^{N\times N}$ 通常初始化为对数矩阵（确保稳定性）。
• $B,C\in {\mathbb{R}}^{N\times d}$ 由输入投影得到。
• 计算复杂度：
• 传统 SSM：$O(L{N}^2)$（$L$ 为序列长度，$N$ 为状态维度）。
• Mamba：$O(LN)$（通过并行扫描和核优化）。

---

6. 总结

Mamba 通过输入依赖的动态参数和硬件感知算法，在保持线性复杂度的同时，实现了对长序列中关键信息的自适应聚焦。在比特币预测中，这种机制使其能快速响应市场突变（如交易量激增、政策变化），同时避免 Transformer 的平方计算开销。CryptoMamba 的 C-Blocks 层级结构进一步增强了多尺度特征提取能力，使其在金融时序预测中达到 SOTA 性能。

2.2Mamba 动态参数计算

一、Mamba 动态参数的核心机制：参数生成器（Parameter Generator）

Mamba 通过参数生成器根据当前输入 $u_k$ 动态计算时变参数（如 $B(u_k)$、$C(u_k)$、时间步长 $\Delta (u_k)$），使系统能够自适应输入内容。参数生成过程通常包含以下步骤：

二、参数计算的数学框架

假设输入 $u_k\in {\mathbb{R}}^D$（D 为输入特征维度，如比特币的 5 个特征：开、高、低、收、成交量），隐藏状态维度为 $N$，则：

1. 输入依赖的 $B(u_k)$ 矩阵生成

• 目标：计算输入矩阵 $B(u_k)\in {\mathbb{R}}^{N\times D}$，描述输入对隐藏状态的影响。
• 生成方法：通过一个小型神经网络（如线性层 + 激活函数）将输入映射到 $B$ 的参数：
  $$B(u_k)=\sigma (W_B\cdot u_k+b_B)\text{或}B(u_k)=\text{Linear}(u_k)$$
• $W_B\in {\mathbb{R}}^{N\times D}$：可学习的权重矩阵；
  • $\sigma$：激活函数（如 ReLU、Sigmoid，用于引入非线性）。

2. 输入依赖的 $C(u_k)$ 矩阵生成

• 目标：计算观测矩阵 $C(u_k)\in {\mathbb{R}}^{1\times N}$，描述隐藏状态对输出的映射。
• 生成方法：类似 $B(u_k)$，通过线性变换或神经网络：
  $$C(u_k)=\text{Linear}(u_k)=W_C\cdot u_k+b_C$$
• $W_C\in {\mathbb{R}}^{1\times D}$：权重向量，将输入转换为观测矩阵的行向量。

3. 时间步长 $\Delta (u_k)$ 动态调整

• 目标：根据输入动态调整离散化时间步长（仅在连续时间模型离散化时使用），例如：
  $$\Delta (u_k)=\text{Softmax}(W_{\Delta }\cdot u_k)\text{或固定为常数（简化场景）}$$

例如：

1. 生成动态参数：
   对每个时间步 $k$，通过线性层生成 $B_k,C_k,{\Delta }_k$：
   $$B_k,C_k=W_B{u}_k+b_B,{\Delta }_k=\text{Softplus}(W_{\Delta }{u}_k+b_{\Delta })$$
   （Softplus 确保 ${\Delta }_k>0$）

2. 离散化：
   计算 ${\bar{A}}_k=e^{{\Delta }_{k}A}$，${\bar{B}}_k=({\Delta }_{k}A{)}^{-1}(e^{{\Delta }_{k}A}-I){\Delta }_k{B}_k$。
   • 若 ${\Delta }_k$ 较大，${\bar{A}}_k$ 趋近于 0，状态快速衰减，更关注近期输入。
   • 若 ${\Delta }_k$ 较小，保留更多历史信息。

三、实例说明：比特币价格预测中的参数计算

假设输入 $u_k$ 是第 $k$ 天的 5 维特征向量：$u_k=[\text{open},\text{high},\text{low},\text{close},\text{volume}]\in {\mathbb{R}}^5$，隐藏状态维度 $N=64$（即 CryptoMamba 中的 d_state=64）。

1. 计算 $B(u_k)$：输入对隐藏状态的影响矩阵

• 步骤 1：线性变换
  $$h_B=W_B\cdot u_k+b_B(W_B\in {\mathbb{R}}^{64\times 5},b_B\in {\mathbb{R}}^{64})$$
• 步骤 2：激活函数（如 Sigmoid，将值缩放到 (0,1)）
  $$B(u_k)=\sigma (h_B)\Rightarrow B(u_k)\in {\mathbb{R}}^{64\times 5}$$
• 实例：高交易量场景
  当 $u_k$ 中的成交量（volume）显著增加时，$h_B$ 对应维度的激活值升高，$B(u_k)$ 中相应行的权重增大，使成交量对隐藏状态的更新贡献增强。

2. 计算 $C(u_k)$：隐藏状态到输出的映射

• 步骤 1：线性变换
  $$C(u_k)=W_C\cdot u_k+b_C(W_C\in {\mathbb{R}}^{1\times 5},b_C\in \mathbb{R})$$
• 实例：价格剧烈波动场景
  当当天价格波动（high - low）较大时，$W_C$ 中对应“波动特征”的权重会增大，使隐藏状态中的“波动信息”对输出（次日收盘价）的影响更显著。

3. 状态转移与观测方程

• 状态转移：
  $$x_k=A\cdot x_{k-1}+B(u_k)\cdot u_k(A\in {\mathbb{R}}^{64\times 64}\text{为固定矩阵，捕获长期趋势惯性})$$
• 观测方程：
  $$y_k=C(u_k)\cdot x_k+D\cdot u_k(D\text{为固定标量，捕获输入对输出的直接影响，如成交量对价格的即时推动})$$

四、动态参数如何影响模型行为？

以比特币价格预测中的“暴跌日”为例（假设 $u_k$ 包含价格暴跌 10%+ 成交量激增 200%）：

1. $B(u_k)$ 的变化：
   • 成交量对应的列权重从 0.2 升至 0.8（因高交易量被识别为关键信号），使 $B(u_k)\cdot u_k$ 中成交量的贡献显著增大，隐藏状态 $x_k$ 快速吸收“暴跌 + 高换手”的风险信号。
2. $C(u_k)$ 的变化：
   • 价格波动对应的权重从 0.3 升至 0.9，使隐藏状态中的“风险信号”在观测方程中被放大，最终预测结果更贴近暴跌后的趋势延续或反弹可能。

五、计算效率：为何动态参数不增加线性复杂度？

• 参数生成复杂度：每个时间步生成 $B(u_k)$ 和 $C(u_k)$ 的计算量为 $O(N\times D)$（仅与隐藏维度 $N$ 和输入维度 $D$ 相关），与序列长度 $L$ 无关。
• 整体复杂度：状态转移的计算为 $O(N^2)$（矩阵乘法），每个时间步总复杂度为 $O(N^2+N\times D)$，最终总复杂度为 $O(L\times (N^2+N\times D))$，仍为线性于序列长度 $L$（对比 Transformer 的 $O(L^2)$）。

六、关键技术细节总结

组件	功能	数学实现	实例中的作用
参数生成器	根据输入动态生成 $B(u_k),C(u_k)$	线性层/神经网络映射	高交易量时增强输入对隐藏状态的影响
固定矩阵 $A$	捕获隐藏状态的长期惯性	可学习的常数矩阵	使隐藏状态保留 80% 的历史趋势（如 $A=0.8I$）
激活函数	引入非线性（可选）	Sigmoid/ReLU	将参数值限制在有效区间（如 (0,1)）
直接输入项 $D$	输入对输出的直接影响	固定标量/可学习参数	成交量直接推动价格（如 $D=0.001$）

七、总结：动态参数如何实现“智能适应”？

Mamba 的动态参数计算本质是通过轻量级的输入映射，让模型在每个时间步灵活调整对“历史信息”和“当前信号”的依赖权重：

• 历史信息：通过固定矩阵 $A$ 捕获长期惯性（如金融市场的趋势延续性）；
• 当前信号：通过动态参数 $B(u_k),C(u_k)$ 聚焦关键输入（如异常波动、高成交量）。

这种机制使 Mamba 既能利用历史数据的长期规律，又能实时响应市场的短期变化，尤其适合比特币等高频、高波动的金融时间序列预测（如 CryptoMamba 在测试期的 RMSE 比传统 SSM 降低 15%）。

5、SSMs与 Mamba区别

传统状态空间模型（SSMs）与 Mamba 的核心区别及 Mamba 的创新点

一、传统 SSMs：线性时不变系统（LTI）

核心特性：

1. 线性系统：状态转移方程和观测方程均为线性关系，即隐藏状态更新和输出生成仅包含线性变换（如矩阵乘法、加法），无非线性激活函数。
   $$x_k=A{x}_{k-1}+B{u}_k,y_k=C{x}_k+D{u}_k$$
   其中 $A,B,C,D$ 为固定参数矩阵，不随输入 $u_k$ 或时间变化。

2. 时不变性（Time-Invariance）：系统动态仅由固定参数决定，与输入内容或时间点无关。例如，今天的状态转移矩阵 $A$ 与明天的 $A$ 完全相同，无法适应系统动态的变化（如市场制度变迁、环境突变）。

局限性：

• 仅能建模线性、稳定的动态系统，无法处理非线性关系（如金融市场的供需失衡导致的价格非线性波动）或时变环境（如监管政策变化导致的市场行为转变）。
• 对复杂场景（如比特币价格的高波动性和制度变迁）建模能力有限，需依赖人为设计特征或多层堆叠，导致参数冗余。

二、Mamba：引入上下文感知的时变 SSM

Mamba 通过三大创新突破传统 SSM 的限制，成为线性高效且自适应的时变系统：

1. 输入依赖参数（Input-Dependent Parameters）

• 核心改进：使 $B,C,\Delta$（时间步长）等参数依赖当前输入 $u_k$，形成时变系统（Time-Varying System）：
  $$x_k=A{x}_{k-1}+B(u_k)u_k,y_k=C(u_k)x_k+D{u}_k$$
  其中 $B(u_k)$ 和 $C(u_k)$ 是根据输入动态计算的矩阵，而非固定值。
• 举例：
  • 在比特币价格预测中，当交易量 $u_k$ 激增（市场活跃）时，$B(u_k)$ 会增大，使当前输入对隐藏状态的影响加强，快速捕捉短期波动；
  • 当价格进入稳定趋势（低波动），$B(u_k)$ 减小，突出历史趋势对当前状态的主导作用（类似“惯性”增强）。

2. 硬件感知算法（Hardware-Aware Algorithm）

• 计算效率：尽管引入动态参数，Mamba 通过优化算法（如利用矩阵快速幂、稀疏计算）保持 线性计算复杂度 $O(L)$（$L$ 为序列长度），与传统 SSM 相同，远低于 Transformer 的 $O(L^2)$。
• 优势：
  • 处理长序列（如 10 年金融数据）时，计算成本不会随序列长度剧烈增长，适合实时预测和大规模数据。

3. 上下文感知的动态适应

• 非线性建模能力：通过输入依赖参数，Mamba 可捕捉非线性动态和制度变迁（Regime Shifts），例如：
  • 当市场从“牛市”转为“熊市”（制度变迁），$C(u_k)$ 会调整观测方程，使隐藏状态对输出的映射从“趋势放大”转为“趋势抑制”；
  • 在语音识别中，面对不同说话人或噪声环境，参数动态调整以优化特征提取。

三、Mamba vs 传统 SSM：核心对比

特性	传统 SSM（LTI）	Mamba（时变 SSM）
参数性质	固定（与输入无关）	动态（随输入 $u_k$ 变化）
系统类型	线性时不变	非线性时变（参数自适应）
计算复杂度	$O(N^{2}L)$（$N$ 为隐藏维度）	$O(L)$（线性于序列长度）
适应场景	稳定、线性动态（如物理系统）	复杂、时变环境（如金融市场、自然语言）
长期依赖建模	依赖固定参数的线性叠加	动态调整参数以强化有效依赖

四、Mamba 的实证优势与应用影响

1. 性能突破：

   • 在语言（如长文本生成）、音频（如语音识别）、基因组（如序列分析）等任务中，Mamba 超越传统 SSM 和 Transformer，证明其在长序列建模中的优越性（文档段落）。
   • 例如，处理 1024 长度的序列时，Mamba 比 Transformer 快 50% 以上，且精度更高。

2. 对时间序列预测的启发（CryptoMamba 设计）：

   • 定制化架构：文档中提出的 CryptoMamba 借鉴 Mamba 的输入依赖动态，设计分层 C-Blocks 结构，使每个 CMBlock 的 Mamba 块能根据比特币价格的历史数据（输入）动态调整参数，捕捉高波动下的短期异常和长期趋势。
   • 轻量化与高效性：保持 Mamba 的线性计算复杂度，参数仅 136k，远低于 Transformer 和 LSTM，适合金融数据的实时处理和部署。

五、总结：Mamba 如何革新 SSM？

Mamba 通过**“动态参数 + 线性效率”**的组合，将传统 SSM 从“固定线性系统”升级为“自适应时变系统”，使其能够：

1. 适应非线性场景：通过输入依赖参数捕捉复杂动态（如金融市场的供需失衡、政策突变）；
2. 高效处理长序列：硬件感知算法确保计算成本可控，适合实时预测；
3. 泛化多领域任务：在语言、音频、金融等领域均表现优异，证明其普适性。

这一创新为时间序列预测（如比特币价格）提供了关键工具——既能利用 SSM 的长期依赖建模优势，又能通过动态参数适应市场的时变性，最终实现精度与效率的双重提升（文档段落）。

汇总（CryptoMamba）

豆包

一、研究背景与核心问题

1. 比特币价格预测的挑战

• 高波动性与复杂性：比特币价格受市场情绪、监管政策、宏观经济等多因素影响，呈现强非线性、非平稳性及制度变迁（Regime Shifts），传统模型难以捕捉长期依赖与动态变化。
• 现有方法的局限性：
  • 传统统计模型（ARIMA、GARCH）：依赖线性假设，无法处理复杂非线性关系和突发 regime shifts。
  • 深度学习模型（LSTM、Transformer）：虽能学习非线性模式，但存在参数冗余、计算复杂度高（如Transformer二次复杂度）及泛化能力不足等问题。
• 创新机遇：状态空间模型（SSM）通过潜变量与观测变量建模时序数据，天然适配金融数据的时间依赖性与随机性；Mamba作为SSM的进阶变体，引入输入依赖动态参数，在保持线性计算效率的同时增强序列建模能力。

2. 研究目标

提出CryptoMamba：首个基于Mamba的SSM框架，旨在解决比特币价格预测中的长期依赖捕捉、高波动适应性及实际交易价值转化问题。

二、数据与方法：CryptoMamba技术框架

1. 数据集与特征工程

• 数据范围：2018.09.17–2024.09.17（共6年），包含5个核心特征：
  • 价格特征：开盘价、收盘价、最高价、最低价（反映每日价格波动）；
  • 交易量：衡量市场活跃度与情绪，首次验证其对预测精度的影响。
• 数据划分：
  • 训练集：2018–2022年（4年），验证集：2022–2023年（1年），测试集：2023–2024年（1年），确保模型在“稳定期”与“高波动期”的泛化能力评估。

2. 模型架构：分层Mamba-SSM设计

• 核心组件：
  • C-Blocks：多层级计算模块，每层包含多个CMBlock（归一化层+Mamba块）与MLP。CMBlock通过Mamba块的输入依赖动态（如参数B、C随输入变化）捕捉序列长期依赖，MLP调整序列长度以实现特征层级融合。
  • Merge块：线性层聚合各C-Blocks输出，生成次日收盘价预测，输入为过去14天数据。
• 技术优势：
  • 长程依赖建模：Mamba块通过连续时间系统离散化，实现O(N)线性计算复杂度，优于Transformer的O(N²)，支持高效处理长序列。
  • 轻量化设计：总参数仅136k，远低于Bi-LSTM（569k）和S-Mamba（330k），减少过拟合风险并适配资源受限环境。

3. 评估指标

• 预测精度：
  • RMSE（均方根误差）：惩罚大误差，适合高波动场景；
  • MAPE（平均绝对百分比误差）：无标度依赖，便于跨时段比较；
  • MAE（平均绝对误差）：平衡误差权重，避免异常值过度影响。
• 交易实用性：通过Vanilla（阈值驱动全仓交易）与Smart（风险区间动态调仓）算法，将预测转化为实际收益，验证模型的市场适应性。

三、实验结果：精度、效率与交易表现

1. 基线模型对比

• 传统递归模型：LSTM、Bi-LSTM、GRU（验证递归架构局限性）；
• 先进SSM模型：S-Mamba（对比同类SSM方法）。

2. 预测精度：CryptoMamba全面领先

模型	RMSE	MAPE (%)	MAE	参数数量	关键结论
CryptoMamba-v	1598.1	2.034	1120.7	136k	含交易量时最优，RMSE较S-Mamba-v低3.2%
S-Mamba-v	1651.6	2.215	1209.7	330k	次优，参数多但精度低于CryptoMamba
Bi-LSTM-v	2080.2	2.738	1562.5	569k	传统模型中最佳，但MAPE比CryptoMamba-v高34.6%
LSTM-v	2202.1	2.896	1668.9	204k	过拟合明显，测试期误差远高于训练期

3. 效率优势：参数少而性能强

• CryptoMamba参数仅为S-Mamba的41%、Bi-LSTM的24%，但RMSE分别降低3.2%、23.2%，证明其架构设计对金融数据的高效特征提取能力。

4. 可视化验证：高波动场景的鲁棒性

• 非Mamba模型（如LSTM、Bi-LSTM）在测试期（2023–2024，高波动）出现显著预测偏差，尤其在价格剧烈波动时（如图2、3）；
• CryptoMamba无论是含/不含交易量，均能紧密跟踪实际价格趋势，显示其对市场动态的强适应性。

5. 实际交易：从预测到收益的转化

• Vanilla算法（阈值=0.01）：
  • 测试期净收益：CryptoMamba-v 246.58美元（初始100美元，回报146.58%），远超S-Mamba-v（182.63美元）和Bi-LSTM-v（122.40美元）。
• Smart算法（风险区间±2%）：
  • 测试期净收益：CryptoMamba-v 213.20美元，通过动态仓位调整平衡风险，收益高于S-Mamba-v（203.17美元）及所有传统模型。
• 关键发现：交易量数据提升所有模型收益，CryptoMamba在稳定期（验证集）与高波动期（测试集）均表现稳健，而S-Mamba在稳定期收益低于初始投资，显示其对简单市场环境的适应性不足。

四、核心贡献与理论价值

1. 方法论创新：
   • 首次将Mamba-SSM应用于加密货币价格预测，构建首个适配金融时序数据的分层SSM架构，突破传统模型对线性关系和短程依赖的局限。
2. 特征工程突破：
   • 验证交易量作为有效预测特征，其引入使CryptoMamba的RMSE降低6.7%、MAPE降低6.2%，为后续研究提供特征选择依据。
3. 效率与实用性平衡：
   • 轻量化设计（136k参数）与高预测精度结合，为实时交易系统部署提供可能，填补“学术模型”与“工业应用”的鸿沟。

五、未来研究方向

1. 模型扩展：
   • 拓展至股票、大宗商品等多资产类别，验证跨金融领域的泛化能力；
   • 融合宏观经济指标（如GDP、利率）、社交媒体情绪等外部数据，增强预测逻辑解释性。
2. 交易策略优化：
   • 设计动态风险控制机制（如止损、仓位管理），提升算法在极端市场条件下的鲁棒性；
   • 结合预测区间（如置信区间）进行概率化交易决策，降低单一预测的不确定性风险。
3. 技术改进：
   • 探索多尺度Mamba块设计，优化不同时间粒度（分钟级、小时级）的高频交易场景；
   • 研究SSM与图神经网络（GNN）的结合，建模加密货币市场与传统金融市场的联动效应。

六、核心数据速查表

维度	指标	CryptoMamba-v（最优）	次优模型（S-Mamba-v）	优势对比
预测精度	RMSE	1598.1	1651.6	↓3.2%
	MAPE (%)	2.034	2.215	↓8.1%
	MAE	1120.7	1209.7	↓7.3%
模型效率	参数数量	136k	330k	↓58%
交易收益	测试期Vanilla（$）	246.58	182.63	+35.0%
	测试期Smart（$）	213.20	203.17	+5.0%

总结

CryptoMamba通过Mamba-SSM的创新架构，在比特币价格预测中实现了精度、效率与实际交易价值的三重突破，为金融时间序列预测提供了新的技术范式。其成功证明了状态空间模型在捕捉复杂金融动态中的独特优势，也为后续多资产预测、量化交易策略开发奠定了方法基础。

kimi

以下是文章《CryptoMamba: Leveraging State Space Models for Accurate Bitcoin Price Prediction》的详细核心内容整理：

I. 引言

1. 研究背景：

   • 比特币价格预测是一个具有挑战性的问题，因为加密货币市场具有高波动性和复杂的非线性动态特性。
   • 传统的时间序列模型（如 ARIMA 和 GARCH）以及深度学习模型（如 LSTM 和 Transformer）在捕捉这些特性时存在局限性。
   • 比特币价格受多种因素影响，包括市场情绪、监管政策和宏观经济趋势，这些因素的交互作用引入了数据的非平稳性。

2. 研究目标：

   • 提出一种基于状态空间模型（SSM）的新型架构 CryptoMamba，用于捕捉金融时间序列中的长期依赖关系。
   • 探讨交易量作为输入特征对预测准确性的影响。
   • 设计交易算法，评估预测模型在实际交易中的应用价值。

II. 相关工作

1. 传统时间序列模型：

   • ARIMA：适用于线性关系建模，但假设数据方差恒定，无法处理时间变化的波动性。
   • GARCH：擅长捕捉波动性聚集，但无法处理非线性和突然的 regime changes（制度变化）。

2. 深度学习模型：

   • LSTM 和 GRU：能够建模序列依赖关系，但在高波动性市场中容易过拟合，且需要大量数据。
   • Bi-LSTM：通过双向建模捕捉更丰富的上下文依赖关系，但同样受限于数据量和过拟合问题。

3. 状态空间模型（SSM）：

   • SSM 通过结合隐藏状态和观测变量，能够有效处理时间序列数据的时序和随机特性。
   • Mamba 模型通过引入选择性机制和动态隐藏状态，进一步提升了 SSM 在序列建模中的能力。

III. 背景知识

1. 状态空间模型（SSM）：
   • SSM 是一种结合了递归神经网络（RNN）和卷积神经网络（CNN）优点的序列模型，特别适合捕捉长期依赖关系。
   • SSM 的数学描述包括连续时间和离散时间两种形式：
     • 连续时间：$\dot{x}=Ax(t)+Bu(t)$，$y(t)=Cx(t)+Du(t)$
     • 离散时间：$x_k=\bar{A}{x}_{k-1}+\bar{B}{u}_k$，$y_k=C{x}_k+D{u}_k$
   • Mamba 模型通过使 $B$、$C$ 和 $\Delta$ 依赖输入，创建了一个时间变化的系统，并通过硬件感知算法保持计算效率。

IV. 方法论

1. 数据集：

   • 使用 Yahoo Finance 提供的每日比特币价格数据，时间范围从 2018 年 9 月 17 日到 2024 年 9 月 17 日。
   • 数据包括开盘价、收盘价、最高价、最低价和交易量。
   • 数据集分为训练集、验证集和测试集，确保模型在未见数据上的泛化能力。

2. CryptoMamba 架构：

   • 核心设计：基于 Mamba 的 SSM 架构，通过多个 C-Block（计算块）和一个 Merge 块组成。
   • C-Block：包含多个 CMBlock 和一个 MLP（多层感知机）。CMBlock 负责特征提取，MLP 调整序列长度。
   • Merge 块：整合所有 C-Block 的输出，生成最终预测。
   • 优势：通过分层结构逐步提炼特征，捕捉短期和长期依赖关系，同时适应金融数据的随机性和动态变化。

3. 评估指标：

   • 使用 RMSE（均方根误差）、MAPE（平均绝对百分比误差）和 MAE（平均绝对误差）评估预测准确性。

V. 实验

1. 实验设置：

   • 比较 CryptoMamba 与多个基线模型（LSTM、Bi-LSTM、GRU 和 S-Mamba）的性能。
   • 模型输入为过去 14 天的数据，输出为次日的收盘价。
   • 使用 Adam 优化器和 RMSE 损失函数，设置早停和学习率调度器以防止过拟合。

2. 实验结果：

   • 预测性能：CryptoMamba 在所有评估指标上均优于基线模型，尤其是在包含交易量数据的版本（CryptoMamba-v）中表现最佳。
     • RMSE：CryptoMamba-v 为 1598.1，显著优于其他模型。
     • MAPE：CryptoMamba-v 为 0.02034，表明预测误差较低。
     • MAE：CryptoMamba-v 为 1120.7，进一步验证了其准确性。
   • 效率：CryptoMamba 仅包含 136k 参数，远低于其他模型（如 Bi-LSTM 的 569k 和 S-Mamba 的 330k），表明其在效率和准确性之间取得了良好的平衡。

3. 交易应用：

   • 使用两种交易算法（Vanilla 和 Smart）模拟交易，初始资金为 100 美元。
   • 结果：CryptoMamba 在验证集和测试集上均实现了最高回报：
     • 测试集：CryptoMamba-v 在 Vanilla 算法下最终余额为 246.58 美元，在 Smart 算法下为 213.20 美元。
     • 结论：CryptoMamba 能够适应不同市场条件（平稳和波动），将准确预测转化为实际收益。

VI. 实际交易应用

1. 交易算法：

   • Vanilla 算法：基于预测价格与当前价格的差异进行简单买卖决策。
   • Smart 算法：引入风险感知机制，通过预测价格的置信区间动态调整交易策略。

2. 交易结果：

   • 在测试期间，CryptoMamba 在两种交易算法下均表现出色，尤其是在高波动性市场中。
   • 验证集：CryptoMamba-v 在 Vanilla 和 Smart 算法下的最终余额分别为 124.09 美元和 127.12 美元。
   • 测试集：CryptoMamba-v 在 Vanilla 和 Smart 算法下的最终余额分别为 246.58 美元和 213.20 美元。

VII. 结论与未来工作

1. 研究结论：

   • CryptoMamba 在比特币价格预测中展现了卓越的准确性和泛化能力，尤其是在包含交易量数据的版本中。
   • 通过交易模拟验证了 CryptoMamba 在实际交易中的实用性，尤其是在高波动性市场中表现出色。

2. 未来工作：

   • 将 CryptoMamba 扩展到其他金融资产（如股票和大宗商品）。
   • 结合情绪分析和宏观经济指标进一步提升预测性能。
   • 探索将风险管理策略融入模型架构中，以增强在高波动市场中的稳健性。

总结

CryptoMamba 是一种创新的状态空间模型架构，专门设计用于金融时间序列预测。它在比特币价格预测中展现了卓越的准确性和泛化能力，并通过交易模拟证明了其在实际应用中的价值。这一研究为金融时间序列预测领域提供了新的方向，特别是在处理高波动性和复杂动态特性方面。