当前位置：首页 > news >正文

C语言（03）——斐波那契数列的理解和运用（超详细版）

news 2025/8/13 6:05:11

斐波那契数列和杨辉三角有着紧密的联系，读者可以阅读以下文章：C语言（04）——杨辉三角的代码实现-CSDN博客

更多优质内容可以订阅下面专栏：

打怪升级之路——C语言之路_ankleless的博客-CSDN博客

Hi！冒险者😎，欢迎闯入 C 语言的奇幻异世界🌌！

我是 Anklelss🧑‍💻，和你一样的闯荡者～这是我的冒险笔记📖，里面有踩过的坑🕳、攒的技能🌟、遇的惊喜🌈，希望能帮你少走弯路✨。

愿我们在代码山峦⛰各自攀登，顶峰碰拳👊，共赏风景呀！🥳

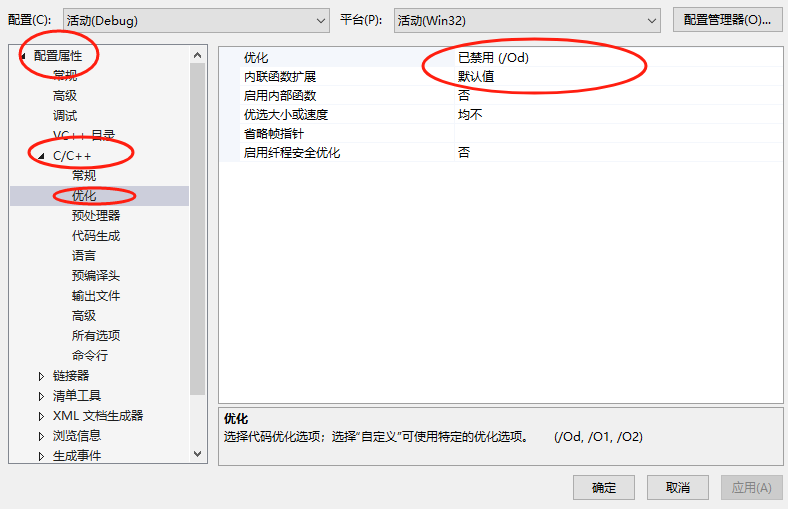
1. 斐波那契数列的背景

1.1 一维斐波那契数列

1.迭代方式

2.递归方式

1.2 斐波那契数列和杨辉三角

1.3 二维斐波那契数列

一. 斐波那契数列的背景

我们先简单了解一下斐波那契数列的故事背景（选择性阅读，可跳至下划线区域）：

斐波那契数列（Fibonacci sequence）是数学中一个著名的序列，因意大利数学家莱昂纳多・斐波那契（Leonardo Fibonacci）在 13 世纪首次系统研究而得名。

但是我们不知道的是，这个伟大的数列来源于一个看似简单的兔子繁殖问题：

“假设一对刚出生的兔子（一雄一雌）需要一个月成熟，成熟后每月能生出一对新兔子（一雄一雌）。如果所有兔子都不会死亡，那么从一对兔子开始，一年后会有多少对兔子？”

第 1 个月：只有 1 对未成熟的兔子（记为F1=1）。
第 2 个月：兔子成熟，仍为 1 对（F2=1）。
第 3 个月：成熟兔子生下 1 对，共 2 对（F3=2）。
第 4 个月：原来的兔子再生 1 对，加上上月出生的兔子成熟，共 3 对（F4=3）。
以此类推，每月的兔子对数恰好满足递推关系Fn=Fn−1+Fn−2，一年后（第 12 个月）的数量为F13=233对。

这个问题的本质是用数学模型描述 “指数级增长” 的现象，而斐波那契数列正是这一模型的抽象结果。

———————————————————————————————————————————

1.1 一维斐波那契数列

他的函数表达形式（一维斐波那契数列）如下：

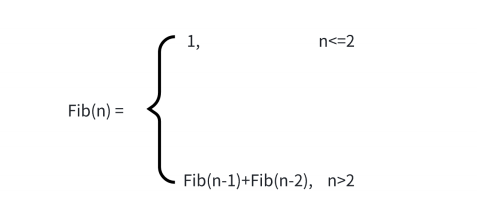
我们可以思考一下他的C语言表达形式，以下是斐波那契数列的两种代码实现方式

1.迭代方式

int fact(int n)
{int a = 1; //使用三个变量记录第n位斐波那契数的计算过程int b = 1; int c = 1; //在n<2时，斐波那契数的值均为1while (n > 2){c = a + b; //a和b相加a = b;b = c;n--;//依次累计计算的数值}return c;
}
int main()
{int n = 0;scanf("%d", &n);int r = fact(n);printf("%d", r);return 0;
}

2.递归方式

递归包含递推和回归两个过程，他们是靠限制条件相互转换。

递归不可以无限递归下去。

#include <stdio.h>
int count = 0;
int Fib(int n)
{if (n == 3)count++;//统计第3个斐波那契数被计算的次数if (n <= 2)return 1;elsereturn Fib(n - 1) + Fib(n - 2);//开始递归，自己使用自己的函数
}
int main()
{int n = 0;scanf("%d", &n);int ret = Fib(n);printf("%d\n", ret);printf("\ncount = %d\n", count);return 0;
}

这两种方式进行对比前，我们知道，循环是一种迭代，但是迭代不仅仅是一种循环。

———————————————————————————————————————————

1.2 二维斐波那契数列

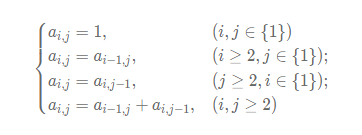
下面是使用迭代法对二维斐波那契数列n位上的值进行计算求解：

#include <stdio.h>
#include <math.h>
#define MOD 1000000007int main()
{int n, m;while(scanf("%d%d", &n, &m)!=EOF){int arr[n + 1][m + 1];for (int i = 1; i < n + 1; i++){for (int j = 1; j < m + 1; j++){if (i == 1 || j == 1){arr[i][j] = 1;}else if (i >= 2 && j == 1){arr[i][j] = arr[i - 1][j] % MOD;}else if (j >= 2 && i == 1){arr[i][j] = arr[i][j - 1] % MOD;}else if (i >= 2 && j >= 2){arr[i][j] = (arr[i - 1][j] + arr[i][j - 1]) % MOD;}}}printf("%d", arr[n][m]);}return 0;
}

递归的代码方式如下：

错误的示范

可以思考一下这串代码的问题

#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define MOD 1000000007int Fact(int arr[1000][1000],int n ,int m)
{if (n == 1 && m == 1){arr[n][m] = 1;}else if (n >= 2 && m == 1){arr[n][m] = arr[n - 1][m] % MOD;}else if (n == 1 && m >= 2){arr[n][m] = arr[n][m - 1] % MOD;}else if (n >= 2 && m >= 2){arr[n][m] = (arr[n - 1][m] + arr[n][m - 1]) % MOD;}return arr[n][m];
}
int main()
{int arr[1000][1000];int n, m;printf("请输入n和m：");scanf("%d%d", &n, &m);//printf("%d %d", n, m);int r = Fact(arr, n, m);printf("%d", r);return 0;
}

上述代码不属于递归的方法运算，且数组的范围空间过大，远大于栈区内存大小

如果将上述代码复制到编译器是否会出现如下的情况？

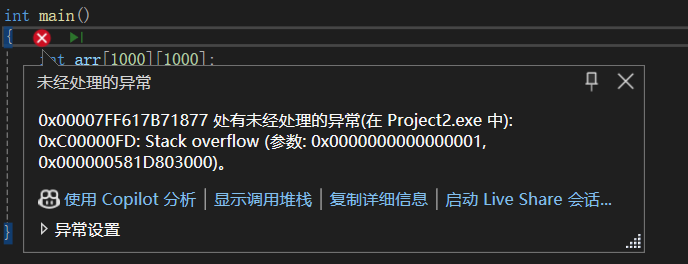
“变量已被优化掉，因而不可用”问题的解决方法如下：

1. 编译器启动了优化，那么关闭的路径：右键点击项目 -> 属性 -> 配置属性 -> C/C++ -> 优化 -> 优化 -> 选择 “已禁用 (/Od)”

2. arr[1000][1000]的定义，栈区的空间大小是有限的，超出了栈区内存也会出现这种情况

那么正确的代码如下：

#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define MOD 1000000007static int Fact(int arr[1000][1000],int n ,int m)
{if (n == 1 && m == 1){arr[n][m] = 1;}else if (n >= 2 && m == 1){arr[n][m] = Fact( arr,n - 1,m) % MOD;}else if (n == 1 && m >= 2){arr[n][m] = Fact(arr, n, m - 1) % MOD;}else if (n >= 2 && m >= 2){arr[n][m] = (Fact(arr, n - 1, m) + Fact(arr, n, m - 1)) % MOD;}return arr[n][m];
}
int main()
{static int arr[1000][1000];int n, m;/*printf("请输入n和m：")*/;scanf("%d%d", &n, &m);//printf("%d %d", n, m);int r = Fact(arr, n, m);printf("%d", r);return 0;
}

代码运行会有栈区满的情况，原因如下：

在代码编译中，采用递归的方式随着递归次数的增加，栈区的内存会被占用，当达到一定次数时，栈区内存无法满足递归时的函数要求，产生栈溢出的情况。

递归和迭代两种方式要辩证使用，根据具体问题具体分析，一般的，递归数量少且迭代不一定能满足逻辑要求时，我们推荐使用递归的方式；当递归数量高时，用迭代可以简化运算次数，提高代码效率，我们推荐使用迭代的方式。

我们学习了动态内存管理malloc之后，可以对上述代码进行如下优化（解决了栈溢出的问题）：

#include <stdio.h>
#include <stdlib.h>
#define MOD 1000000007int main() {int n, m;while (scanf("%d%d", &n, &m) != EOF) {if (n < 1 || m < 1) {printf("n和m需为正整数\n");continue;}// 动态分配二维数组（堆区，避免栈溢出）int** arr = (int**)malloc((n + 1) * sizeof(int*));for (int i = 0; i <= n; i++) {arr[i] = (int*)malloc((m + 1) * sizeof(int));}// 填充边界值for (int i = 1; i <= n; i++) arr[i][1] = 1;for (int j = 1; j <= m; j++) arr[1][j] = 1;// 迭代计算内部值for (int i = 2; i <= n; i++) {for (int j = 2; j <= m; j++) {arr[i][j] = (arr[i - 1][j] + arr[i][j - 1]) % MOD;}}printf("%d\n", arr[n][m]);// 释放内存for (int i = 0; i <= n; i++) free(arr[i]);free(arr);}return 0;
}

代码动态地使用堆区内存，在实现要求后释放内存空间，避免了浪费内存以及栈溢出情况。

———————————————————————————————————————————

1.3 斐波那契数列和杨辉三角

在递归这种方式中，当我们想知道第n项斐波那契数时，他的计算式是如下排布的

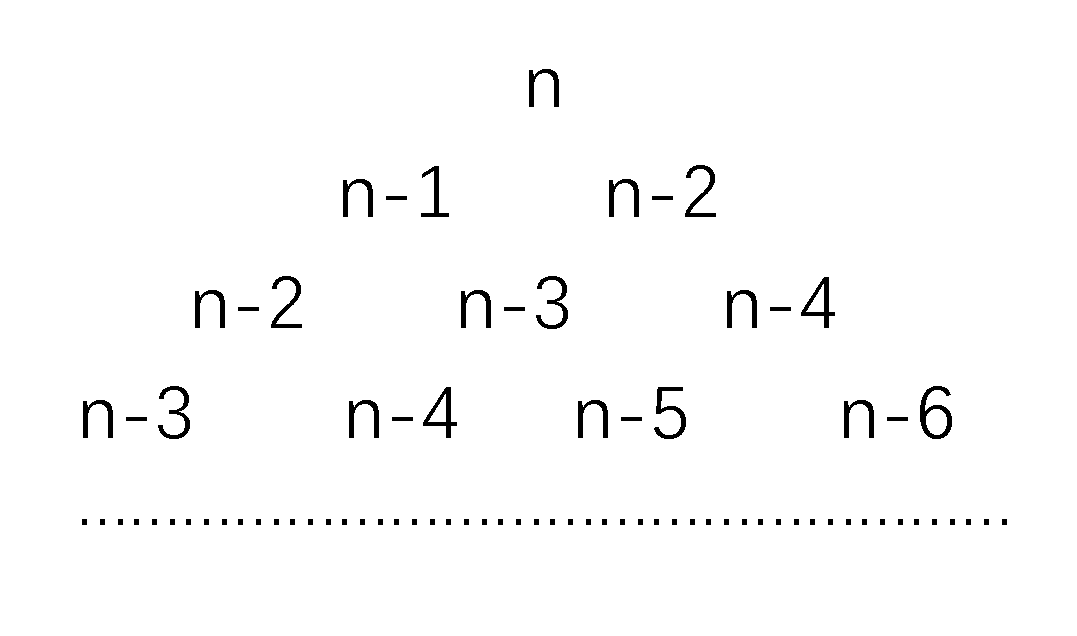
从这样的表达形式中，我们可以联想到另一个重要的数学理论————杨辉三角。

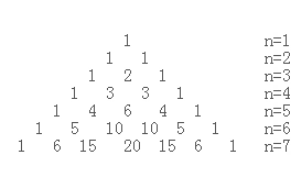
杨辉三角和斐波那契数列最明显的一个特征就是，他们按照一定规律展开排布时，他们每行的元素个数保持一致，呈三角形向下分布。

斐波那契数列可以通过杨辉三角求和得到：

斐波那契数列的第n项F(n)，等于杨辉三角中 “从顶部到第n−1行的左斜对角线元素之和”。例如：

F(5)=5=C(4,0)+C(3,1)+C(2,2)=1+3+1
F(6)=8=C(5,0)+C(4,1)+C(3,2)=1+4+3

二者均以简单的递推规则生成复杂的序列 / 结构，体现了数学中 “简单规则孕育复杂系统” 的普遍规律，是递归思想在不同维度的典型应用。

二、斐波那契数列的高效计算：矩阵快速幂算法（原理与实现）

在计算斐波那契数列时，当n取值极大（如n=10^6甚至n=10^9），迭代法的O(n)时间复杂度仍会显得低效。而矩阵快速幂算法通过将递推关系转化为矩阵幂运算，结合 “快速幂” 技巧，可将时间复杂度降至O(log n)，成为处理超大n的最优解。本节将详细拆解其原理。

2.1 矩阵快速幂的核心：用矩阵表示递推关系

斐波那契数列的递推公式是F(n) = F(n-1) + F(n-2)（F(1)=1, F(2)=1）。这种 “线性递推关系” 可以用矩阵乘法表示，这是矩阵快速幂的基础。

2.1.1 从递推公式到矩阵乘法

观察斐波那契数列的相邻两项关系：

F(n) = 1*F(n-1) + 1*F(n-2)（递推公式本身）
F(n-1) = 1*F(n-1) + 0*F(n-2)（前一项自身）

这两个等式可以合并为一个矩阵乘法表达式：

plaintext

| F(n)   |   =   | 1 1 |   *   | F(n-1) |
| F(n-1) |       | 1 0 |       | F(n-2) |

我们称矩阵[[1,1],[1,0]]为 “转换矩阵”（记为M）。它的作用是将[F(n-1), F(n-2)]“转换” 为[F(n), F(n-1)]。

2.1.2 递推的矩阵幂形式

通过重复应用上述矩阵乘法，可将递推关系扩展到更早期的项。例如：

计算F(3)：

plaintext

| F(3) |   = M * | F(2) |   = M * | 1 |
| F(2) |       | F(1) |       | 1 |

计算F(4)：

plaintext

| F(4) |   = M * | F(3) |   = M * (M * | F(2) |) = M² * | F(2) |
| F(3) |       | F(2) |             | F(1) |       | F(1) |

推广到F(n)（n≥2）：

plaintext

| F(n)   |   = M^(n-2) * | F(2) |   = M^(n-2) * | 1 |
| F(n-1) |               | F(1) |           | 1 |

其中M^(n-2)表示转换矩阵M的n-2次幂。这意味着：斐波那契数列的第n项，可通过计算转换矩阵的n-2次幂，再与初始向量[F(2), F(1)]相乘得到。

2.2 快速幂：高效计算矩阵的幂

矩阵幂运算M^k（如M^(n-2)）直接计算需要k-1次矩阵乘法（时间复杂度O(k)），仍不够高效。而 “快速幂” 算法通过二进制分解，可将计算次数降至O(log k)。

2.2.1 快速幂的核心思想：二进制分解

任何正整数k都可以表示为二进制形式（如10 = 8 + 2 = 2³ + 2¹）。因此，M^k可分解为多个 “M的 2ⁿ次幂” 的乘积：

plaintext

M^10 = M^(8 + 2) = M^8 * M^2

这样，计算M^10只需 2 次乘法（M^2和M^8），而非 9 次（M*M*...*M）。

2.2.2 快速幂的步骤（以`M^k`为例）

初始化结果：设res为 “单位矩阵”（类似乘法中的 “1”，与任何矩阵相乘都不改变其值）。
分解k的二进制：从k的最低位开始，依次判断每一位是否为 1：
- 若当前位为 1，则res = res * 当前的矩阵幂；
- 无论当前位是否为 1，都将 “当前的矩阵幂” 平方（即M^(2^i)→M^(2^(i+1))），并将k右移一位（处理下一个二进制位）。
终止条件：当k减为 0 时，res即为M^k。

2.2.3 示例：计算`M^5`（`5`的二进制为`101`）

初始：res = 单位矩阵，当前矩阵幂 = M^1，k=5（二进制101）。
第 1 步：k的最低位为 1（5%2=1），则res = res * M^1 = M^1；当前矩阵幂平方为M^2；k=5>>1=2（二进制10）。
第 2 步：k的最低位为 0（2%2=0），res不变；当前矩阵幂平方为M^4；k=2>>1=1（二进制1）。
第 3 步：k的最低位为 1（1%2=1），则res = res * M^4 = M^1 * M^4 = M^5；当前矩阵幂平方为M^8；k=1>>1=0，终止。
结果：res = M^5，仅用 2 次矩阵乘法（M^1*M^4）。

2.3 矩阵快速幂计算斐波那契数列的完整流程

结合上述原理，计算F(n)的步骤如下：

若n≤2，直接返回 1（初始条件）。
否则，计算转换矩阵M = [[1,1],[1,0]]的n-2次幂（M^(n-2)）。
用M^(n-2)乘以初始向量[F(2), F(1)] = [1,1]，结果的第一个元素即为F(n)。

2.4 为什么矩阵快速幂更高效？

迭代法计算F(n)需要n-2次加法，时间复杂度O(n)；
矩阵快速幂通过二进制分解，仅需O(log n)次矩阵乘法（每次矩阵乘法包含 4 次乘法和 2 次加法），时间复杂度O(log n)。

当n=10^9时，迭代法需要 10 亿次运算，而矩阵快速幂仅需约 30 次运算（log2(10^9)≈30），效率提升极为显著。

2.5 矩阵快速幂的 C 语言实现（结合原理）

以下代码严格对应上述原理，包含矩阵乘法、快速幂和斐波那契计算三个核心部分：

#include <stdio.h>// 定义2x2矩阵（存储斐波那契转换矩阵）
typedef struct {long long m[2][2]; // 用long long避免溢出
} Matrix;// 矩阵乘法：计算a * b，结果存入res
Matrix multiply(Matrix a, Matrix b) {Matrix res;// 按矩阵乘法规则计算每个元素res.m[0][0] = a.m[0][0] * b.m[0][0] + a.m[0][1] * b.m[1][0];res.m[0][1] = a.m[0][0] * b.m[0][1] + a.m[0][1] * b.m[1][1];res.m[1][0] = a.m[1][0] * b.m[0][0] + a.m[1][1] * b.m[1][0];res.m[1][1] = a.m[1][0] * b.m[0][1] + a.m[1][1] * b.m[1][1];return res;
}// 快速幂：计算mat的power次幂
Matrix matrix_pow(Matrix mat, int power) {// 单位矩阵：初始结果（类似乘法中的1）Matrix res = {{1, 0}, {0, 1}}; while (power > 0) {if (power % 2 == 1) { // 当前二进制位为1，乘以当前矩阵幂res = multiply(res, mat);}mat = multiply(mat, mat); // 矩阵平方（幂次翻倍）power /= 2; // 处理下一个二进制位}return res;
}// 计算斐波那契数列第n项
long long fib_matrix(int n) {if (n <= 2) return 1;Matrix M = {{1, 1}, {1, 0}}; // 转换矩阵Matrix M_power = matrix_pow(M, n - 2); // 计算M^(n-2)// 结果 = M^(n-2) * [1, 1]^T 的第一个元素return M_power.m[0][0] * 1 + M_power.m[0][1] * 1;
}int main() {int n;printf("请输入n: ");scanf("%d", &n);if (n < 1) {printf("n必须为正整数\n");return 1;}printf("F(%d) = %lld\n", n, fib_matrix(n));return 0;
}