数据结构和算法学习记录——平衡二叉树(基本介绍、平衡因子、平衡二叉树的定义、平衡二叉树的高度)
目录
基本介绍
平衡因子
平衡二叉树
平衡二叉树的高度
基本介绍
什么是平衡二叉树?
以一个例子来解释一下:
搜索树结点按不同的插入次序,将会导致不同的深度和平均查找长度ASL
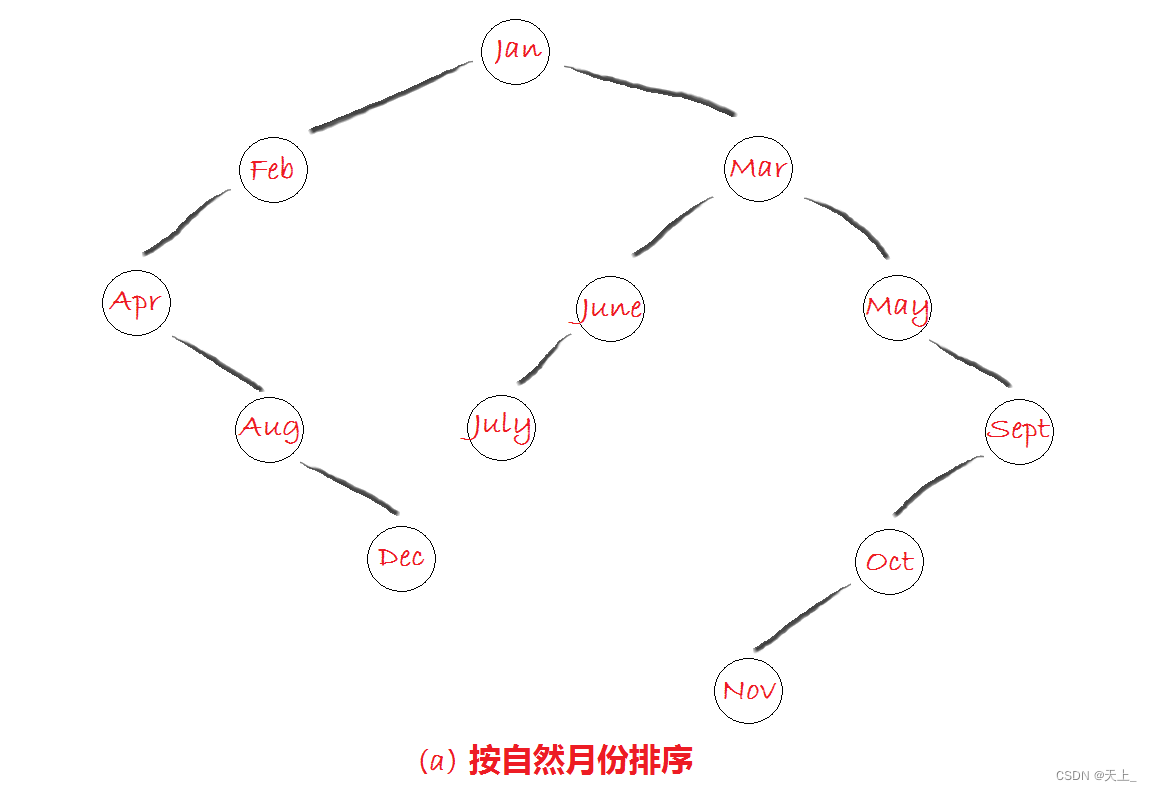
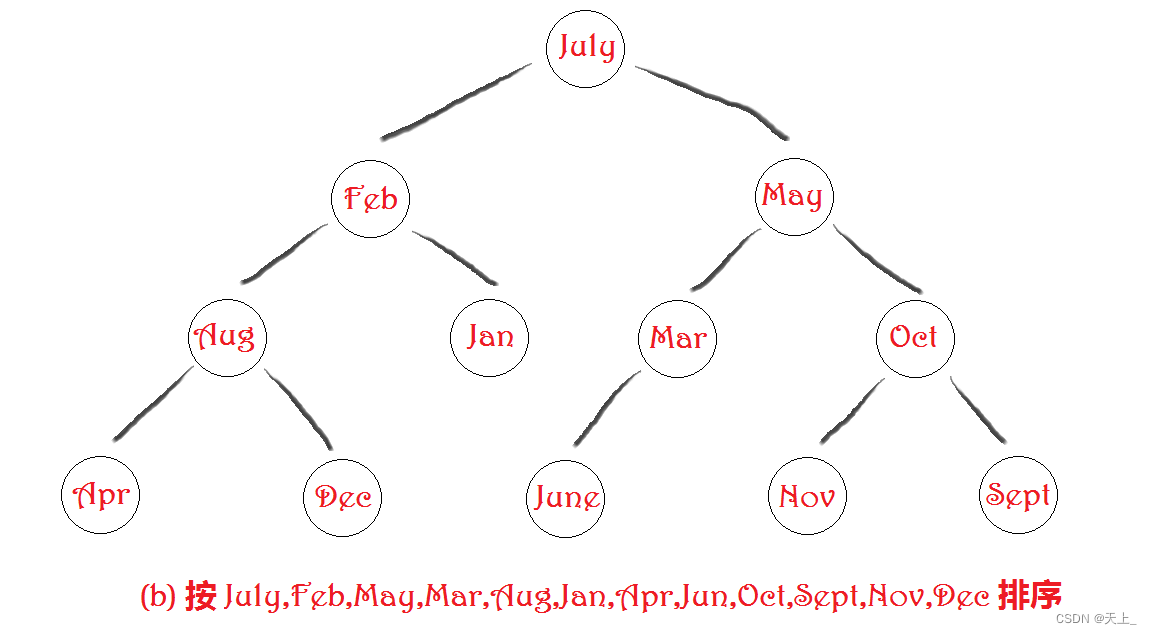

在二叉搜索树中查找一个元素:
(a)要找到Jan,需要查找一次;要找到Feb,需要查找两次;
要找到Mar,也需要查找两次......要找到Nov,需要查找六次。
把所有查找次数加起来,再除以12,
得到平均查找长度:ASL(a) = ( 1 + 2 * 2 + 3 * 3 + 4 * 3 + 5 * 2 + 6 * 1 ) / 12 = 3.5
(b)要找到July,需要查找一次;要找到Feb,需要查找两次;
要找到May,也需要查找两次......要找到Sept,需要查找四次。
算出平均查找长度:ASL(b) = (1 + 2 * 2 + 3 * 4 + 4 * 5) / 12 = 3.0
(c)要找到Apr,需要查找一次;要找到Aug,需要查找两次......
要找到Sept,需要查找十二次。
算出平均查找长度:ASL(c) = ( 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12) / 12 = 6.5
通过上面的例子,我们可以看到方式b的平均查找长度最短,在观感上结点的分布也比较均匀。
所以二叉树,我们要求比较平衡,才能够让查找的长度更短一些。
而如何衡量一颗二叉树平衡不平衡呢?
- 是左右两边的结点数差不多
- 是左右两边的高度差不多
这样我们就认为基本上平衡,即为平衡二叉树。
平衡因子
平衡因子(Balance Factor,简称BF):
BF(T) =
-
, 其中
和
分别为T的左、右子树的高度。
平衡二叉树
平衡二叉树(Balanced Binary Tree) (AVL树)
空树,或者任一结点左、右子树高度差的绝对值不超过1,即
下面来判断一下以下几颗二叉树是否为平衡二叉树:
(1)
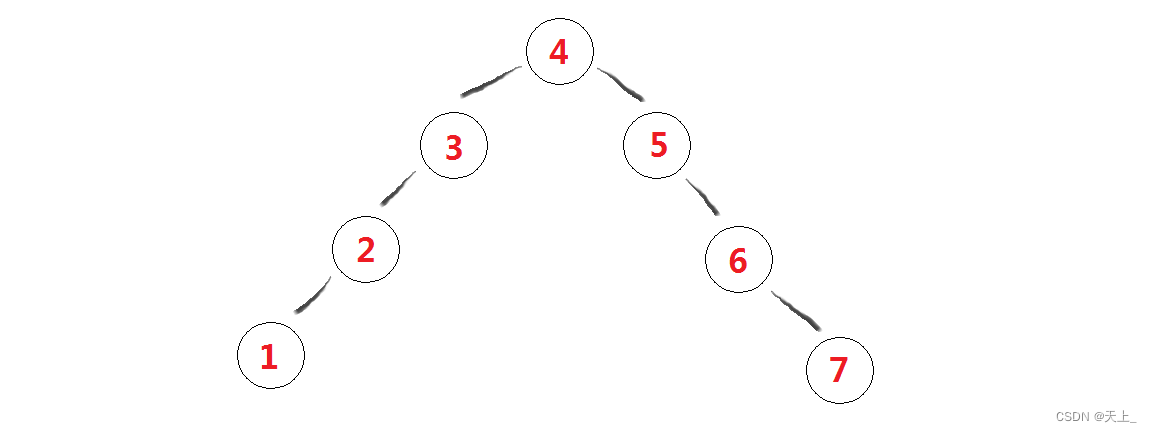
(2)
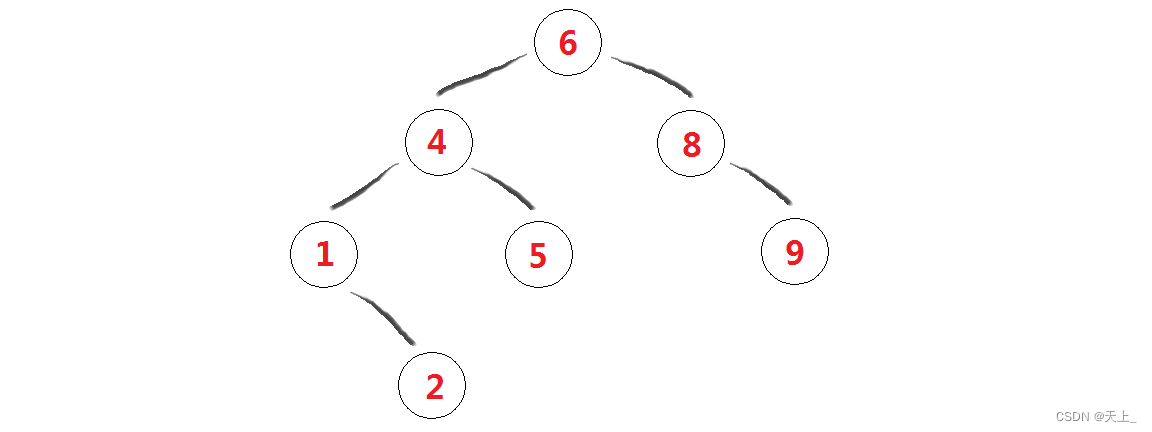
(3)
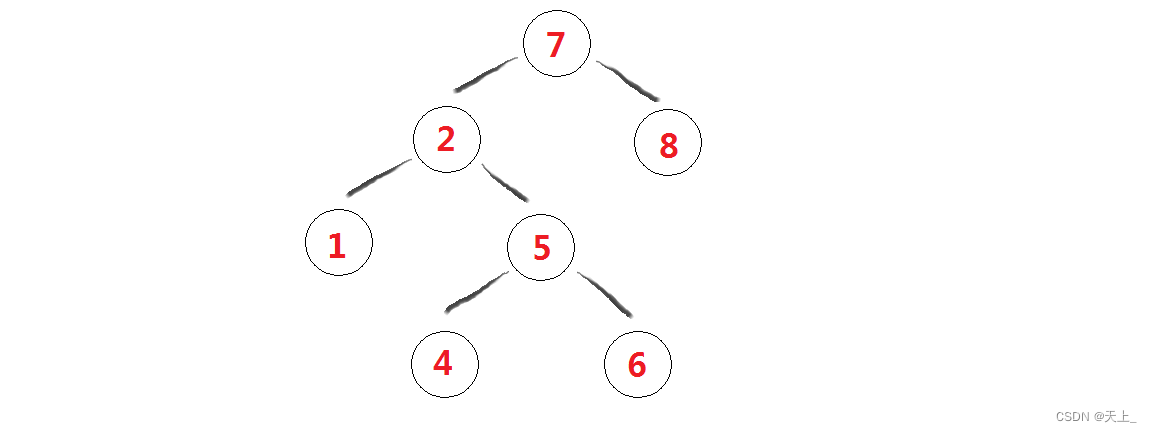
先来看第一棵二叉搜索树:

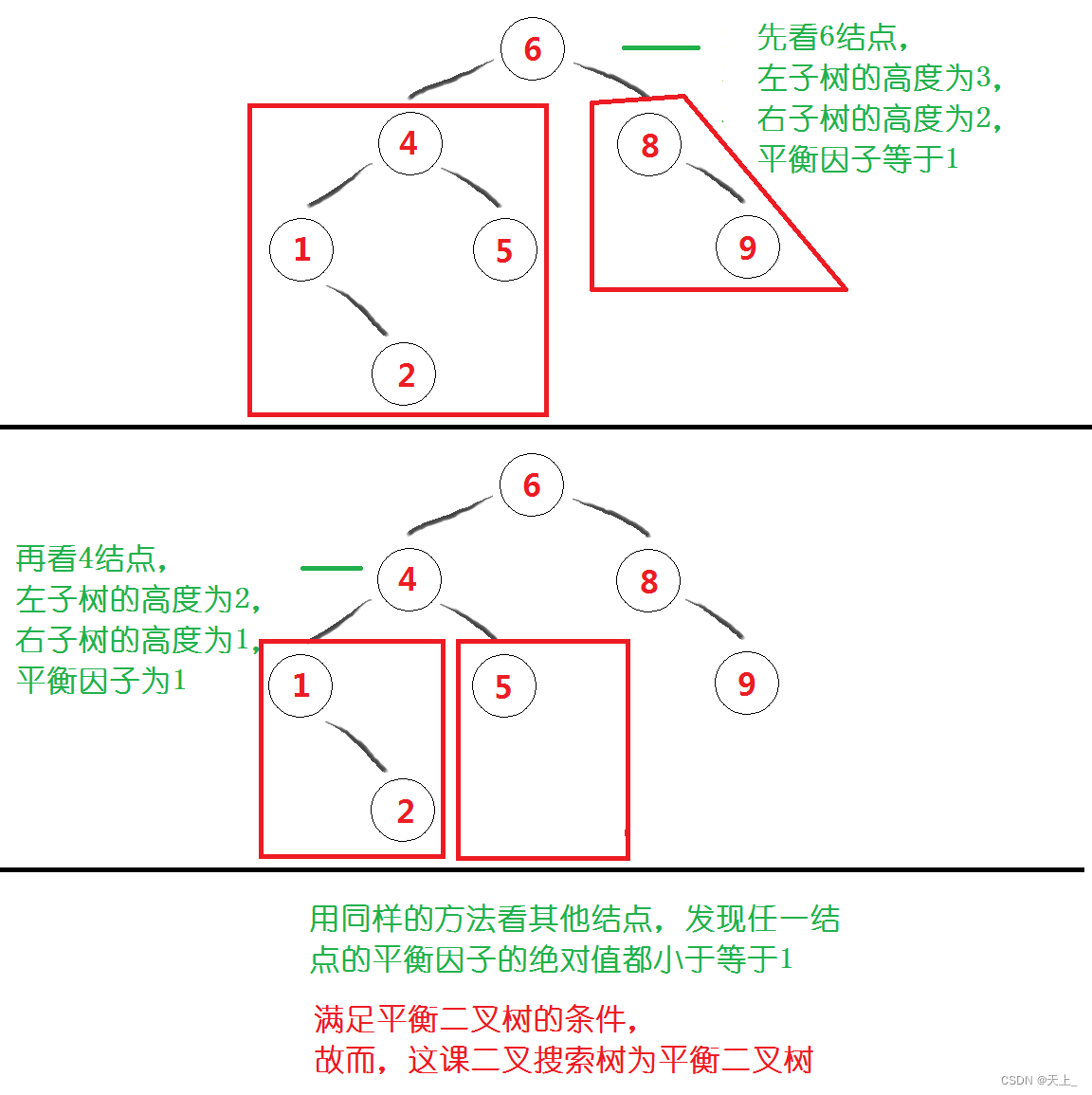
再来看第二棵二叉搜索树:
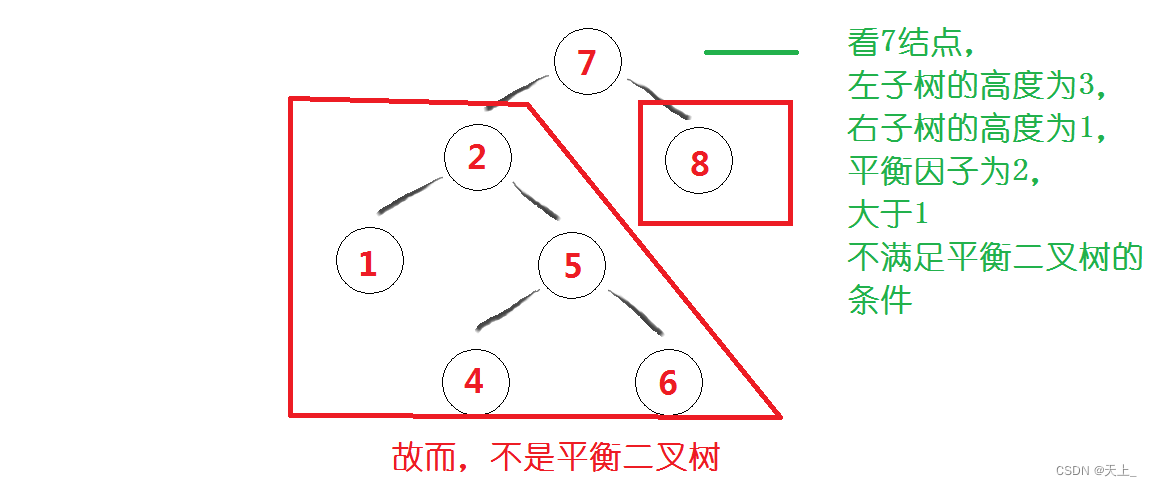
最后看第三棵二叉搜索树:
平衡二叉树的高度
我们要二叉树平衡,其目的是为了让二叉树的高度更低一些,
越平衡的二叉树高度就越低。
一棵结点总数为n的完全二叉树高度为 h = log2n,

那么平衡二叉树的高度是否能达到呢?
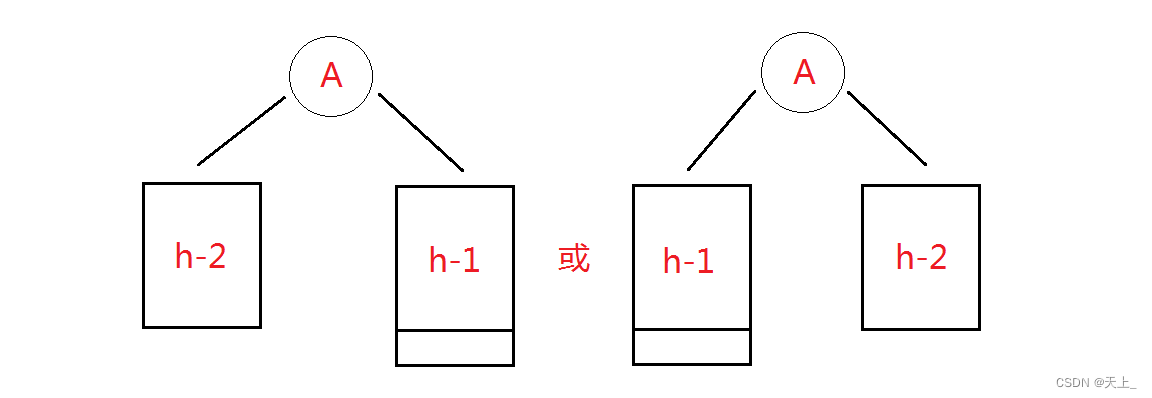
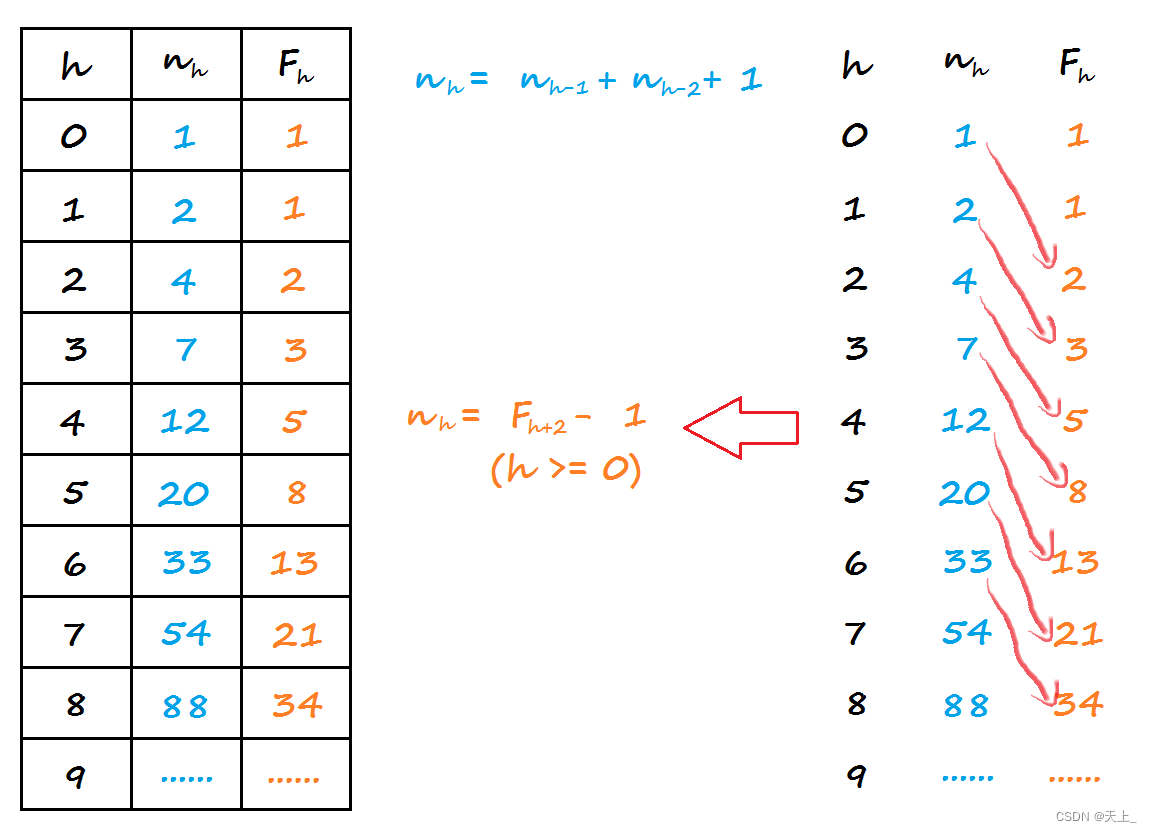
设为 高度为h的平衡二叉树的最少结点数。 结点数最少时:

总结出:
可以得到一个公式:
我们会发现,这个公式有点眼熟,是与斐波那契序列的公式有点像。
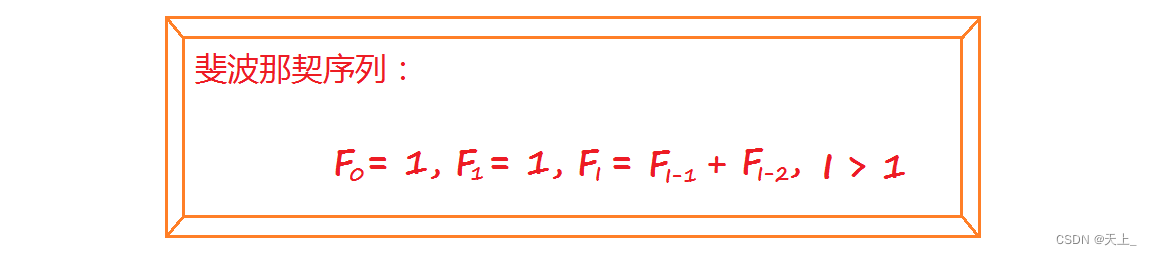
从这里我们就来分析一下nh跟斐波那契序列的有什么关系。
在数学上,有一个公式:
当i逐步增大时,大致等于公式算出来的值。
且是一个指数函数。
根据我们上面分析出来的和
的关系,就可以代入得到
的相关公式。
所以反过来我们就得到h的表达式:
用自己的想法把他推一遍:

综上所述,我们可以得到结论:
给定结点数为n的AVL树的最大高度为
end
学习自:MOOC数据结构——陈越、何钦铭
