【浓缩概率】浓缩概率思想帮我蒙选择题的概率大大提升!
今天在学习的时候遇到一个很有趣的思想叫作浓缩概率,可以帮我们快速解决一下概率悖论问题!
什么是概率
计算概率有下面两个最简单的原则:
原则一、计算概率一定要有一个参照系,称作「样本空间」,即随机事件可能出现的所有结果。事件 A 发生的概率 = A 包含的样本点 / 样本空间的样本总数。
原则二、计算概率一定要明白,概率是一个连续的整体,不可以把连续的概率分割开,也就是所谓的条件概率。
三门问题
问题1:
游戏参与者面对三扇门,其中两扇门后面是山羊,一扇门后面是跑车
你是游戏参与者,现在有门 1,2,3,假设你随机选择了门 1,然后主持人打开了门 3 告诉你那后面是山羊。现在,你是坚持你最初的选择门 1,还是选择换成门 2 呢?
答案1:
是应该换门,换门之后抽到跑车的概率是 2/3,不换的话是 1/3
解释1 :
主持人开门实际上在「浓缩」概率。一开始你选择到跑车的概率当然是 1/3,剩下两个门中包含跑车的概率当然是 2/3,这没啥可说的。但是主持人帮你排除了一个含有山羊的门,相当于把那 2/3 的概率浓缩到了剩下的这一扇门上。那么,你说你是抱着原来那扇 1/3 的门,还是换成那扇经过「浓缩」的 2/3 概率的门呢?
选择题
如果你看懂了上题的思想,那么
问题2:
你蒙选择题,先蒙了 A,后来灵机一动排除了 B 和 C,请问你是否要把 A 换成 D?
答案2:
换!
解释2:
当你蒙A的概率是1/4,那么答案在另外三个的概率是3/4,但是你巧妙的排除了B和C,那么3/4的概率就落在了D上了,你应该选D还是选A,答案就很清楚了。
问题3:
也许读者会问,如果只排除了一个答案,比如说 B,那么我是否应该把 A 换成 C 或者 D 呢?答案是,换!
答案3:
因为按照刚才「浓缩」概率这个思想,只要进行了排除,都是在进行「浓缩」,均摊下来肯定比你一开始蒙的那个答案概率 1/4 高。比如刚才的例子,C 和 D 的正确概率都是 3/8(3/4 * 1/2),而你开始蒙的 A 只有 1/4。
使用前提:
运用此策略蒙题的前提是你真的抓瞎,真的随机乱选答案,这样概率才能作为最后的杀手锏。
其他反直觉的概率问题
男孩女孩问题
假设有一个家庭,有两个孩子,现在告诉你其中有一个男孩,请问另一个也是男孩的概率是多少?
有两个孩子,那么样本空间为 4,即哥哥妹妹,哥哥弟弟,姐姐妹妹,姐姐弟弟这四种情况。已知有一个男孩,那么排除姐姐妹妹这种情况,所以样本空间变成 3。另一个孩子也是男孩只有哥哥弟弟这 1 种情况,所以概率为 1/3
生日悖论
屋子里需要有多少人,才能使得存在至少两个人生日是同一天的概率达到 50%?
答案是 23 个人,也就是说房子里如果有 23 个人,那么就有 50% 的概率会存在两个人生日相同。
只有 1 个人的时候,生日唯一的概率是 365/365,2 个人时,生日唯一的概率是 365/365 × 364/365,以此类推可知 23 人的生日都唯一的概率
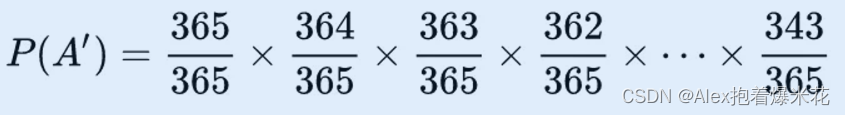
摸球问题
一号箱子有 4 个黑球 2 个红球,二号箱子有 2 个黑球 4 个红球,随便选一个箱子,随便摸一个球,问你摸出红球的概率。
对于不知情的小明,他会随机选择一个箱子,随机摸球,摸到红球的概率是:1/2 × 2/6 + 1/2 × 4/6 = 1/2
对于知情的你,你知道在二号箱子摸球概率大,所以只在二号箱摸,摸到红球的概率是:0 × 2/6 + 1 × 4/6 = 2/3
