AcWing 6479. 点格棋

我个人觉着难度省选-普及+

难度：简单

时/空限制：0.4s / 64MB

总通过数：236

总尝试数：610

来源： 2025 睿抗机器人开发者大赛CAIP-编程技能赛-本科组（省赛）

点格棋（Dots and Boxes，又名Boxe、 Squares、Paddocks、Square-it Dots and Dashes、Dots、Smart Dots、Dot Boxing、the Dot Game），或译围地盘，是法国数学家爱德华·卢卡斯在 18911891 年推出的两人纸笔游戏。

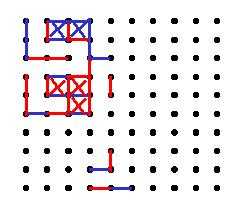
图作者：Yonidebest，来自维基百科

游戏从一个空的 N×M的由点构成的网格图开始（如上图）。

两个玩家轮流进行回合，每回合玩家需要在两个未连接的相邻点之间添加一条水平线或垂直线。

完成每个 1×1方框的最后一条边的玩家获得 11 分，且如当前回合获得了分数，则额外再进行另一回合。

当无法添加线时，游戏结束。

获胜者是得分最高的玩家。

一个典型的游戏过程如下。

注意我们省略了第 8到第 9 步中间的 A 的额外回合。

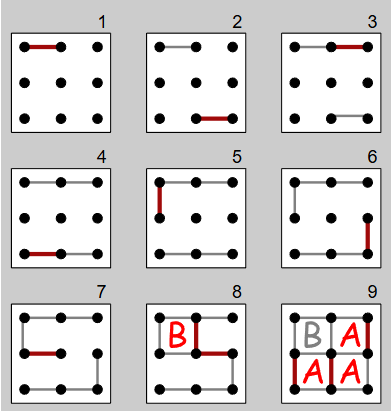
图作者：Tiger6，来自维基百科

小 A 和 小 B 在玩点格棋，并记录下了他们的游戏步骤。

你需要检查他们记录的步骤是否存在问题，并输出最终的得分及获胜者。

输入格式

输入第一行是三个正整数 N,M,S，表示棋盘共有 N行，每行共有 M 个点，记录下来的游戏步骤共有 S步。

接下来的 S行，每行分别是五个整数，其中第一个整数为 0或者 1：0 表示该步由小 A执行，1 表示该步由小 B 执行。后面的四个整数 Startx,Starty,Endx,Endy表示该步的执行者将 (Startx,Starty)与 (Endx,Endy)的两个点之间连接了一条线。

左上角的点坐标为 (1,1)(1,1)。

额外的规则如下：

• 开始时棋盘为空。
• 小 A 应当是先手方。
• 所有存在问题的步骤在记录后跳过即可（不影响棋盘）。
• 结束时可以存在还有合法连线未完成的情况。
• 如两方得分一致，则视为小 B（后手方）赢得比赛。

输出格式

输出第一行是所有有问题的步骤编号，用一个空格隔开。编号按输入顺序从 1 开始编号，输出时升序输出。如果所有步骤都没有问题，输出一个 -1。

第二行输出两个整数，第一个为获胜的玩家，0 表示小 A，1 表示小 B；第二个为最后获胜者获得的分数。

数据范围

1≤N,M≤100
1≤S≤105

输入样例1：

3 3 12
0 1 1 1 2
1 3 3 3 2
0 1 2 1 3
1 3 1 3 2
0 1 1 2 1
1 2 3 3 3
0 2 1 2 2
1 1 2 2 2
1 2 2 2 3
0 1 3 2 3
0 2 2 3 2
0 2 1 3 1

输出样例1：

-1
0 3

输入样例2：

3 3 16
1 1 1 1 2
0 1 1 1 2
1 3 3 2 2
1 3 3 3 2
0 1 2 1 3
1 3 1 3 2
0 1 1 2 1
1 2 3 3 3
0 2 1 2 2
1 2 1 2 2
1 1 2 2 2
0 2 2 2 3
1 2 2 2 3
0 1 3 2 3
0 2 2 3 2
0 2 1 3 1

输出样例2：

1 3 10 12
0 3

题目大意
点格棋以 N×M 的点阵为棋盘，两名玩家轮流连接相邻两点（水平或垂直）。若某一步恰好完成一个 1×1 方框的第四条边，该玩家得 1 分且可额外再走一回合。代码需：
1.检查每步操作的合法性（如是否为当前玩家、是否连接相邻点、是否重复连线等）。

2.记录合法操作并计算得分。
3.输出所有非法步骤及最终获胜者。
关键变量与数据结构
st[N][N][4]：三维数组，用于标记某条边是否已存在。
前两维 (x,y) 表示点的坐标（左上角为 (1,1)）。
第三维 d 表示方向（0：上，1：右，2：下，3：左），对应方向向量 dx = [-1,0,1,0]，dy = [0,1,0,-1]。
player：当前应行动的玩家（0 为小 A，1 为小 B，初始为 0 因为小 A 先手）。
a, b：分别记录小 A 和小 B 的得分。
exists：标记是否存在非法步骤。
核心函数解析
1. get_dir(x1, y1, x2, y2)：判断两点间的方向
输入两个点的坐标，返回两点间的方向 d（0-3 对应上、右、下、左）。
若两点不相邻（非水平 / 垂直相邻），返回 -1（非法边）。
2. calc_score(x, y, d)：计算添加一条边后新增的得分
一条边可能属于 两个 1×1 方框（例如中间的边可能是上方方框的下边和下方方框的上边）。函数逻辑：
  若方向 d 为 2（下）或 3（左），转换为其相反方向（0 或 1），统一处理上、右方向的边。
  对方向 d=0（上）：检查是否形成左侧或右侧的方框（需另外三条边已存在）。
  对方向 d=1（右）：检查是否形成上方或下方的方框（需另外三条边已存在）。
  返回新增的得分（0、1 或 2）。
主逻辑流程（main 函数）
1.读取输入：棋盘尺寸 N, M 和步骤数 S。
2.处理每一步：
读取当前步骤的玩家 t、起点 (x1,y1)、终点 (x2,y2)。
调用 get_dir 获取方向 d，判断步骤是否合法：
非法情况：d=-1（非相邻点）、t≠player（非当前玩家）、st[x1][y1][d]=true（边已存在）。
合法情况：标记边为存在（双向标记，如 (x1,y1) 的方向 d 和 (x2,y2) 的方向 d^2），计算得分并更新玩家分数。若得分不为 0，当前玩家继续行动；否则切换玩家。
3.输出结果：
若有非法步骤，按顺序输出编号；否则输出 -1。
比较得分：a > b 则小 A（0）获胜，否则小 B（1）获胜（得分相等时小 B 赢），输出获胜者及分数。
示例说明
  样例 1：所有步骤合法，小 A 得 3 分，输出 -1 和 0 3。
  样例 2：步骤 1（非先手）、3（非法边）、10（重复连线）、12（非当前玩家）非法，最终小 A   得 3 分，输出非法步骤编号和 0 3。

代码如下

#include <bits/stdc++.h>
using namespace std;const int N = 110;
int n, m, s;
bool st[N][N][4];  // 记录边是否存在：0上、1右、2下、3左
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};  // 方向向量// 获取两点间的方向（0-3），不相邻则返回-1
int get_dir(int x1, int y1, int x2, int y2) {for (int i = 0; i < 4; i++) {if (x1 + dx[i] == x2 && y1 + dy[i] == y2)  // 修正y方向判断return i;}return -1;
}// 计算新增的分数
int calc_score(int x, int y, int d) {if (d > 1) {  // 若方向是下（2）或左（3），转换为上（0）或右（1）处理x += dx[d];y += dy[d];d ^= 2;  // 2^2=0，3^2=1（取反方向）}int res = 0;if (d == 0) {  // 上边：可能属于下方两个方框// 左侧方框（x,y）的上边if (st[x][y][3] && st[x-1][y][3] && st[x][y-1][0]) res++;// 右侧方框（x,y+1）的上边if (st[x][y][1] && st[x-1][y][1] && st[x][y+1][0]) res++;} else {  // 右边：可能属于左侧两个方框// 上方方框（x,y）的右边if (st[x][y][0] && st[x][y+1][0] && st[x-1][y][1]) res++;// 下方方框（x+1,y）的右边if (st[x][y][2] && st[x][y+1][2] && st[x+1][y][1]) res++;}return res;
}int main() {cin >> n >> m >> s;int player = 0;  // 先手为小A（0）int a = 0, b = 0;  // 得分vector<int> errors;  // 存储错误步骤编号for (int i = 1; i <= s; i++) {int t, x1, y1, x2, y2;cin >> t >> x1 >> y1 >> x2 >> y2;int d = get_dir(x1, y1, x2, y2);// 检查步骤是否合法if (d == -1 || t != player || st[x1][y1][d]) {errors.push_back(i);} else {// 标记边存在（双向记录）st[x1][y1][d] = true;st[x2][y2][d ^ 2] = true;  // 反方向标记// 计算得分int score = calc_score(x1, y1, d);if (score) {  // 得分则当前玩家继续if (player == 0) a += score;else b += score;} else {  // 不得分则切换玩家player ^= 1;}}}// 输出错误步骤if (errors.empty()) {cout << -1 << endl;} else {for (int i = 0; i < errors.size(); i++) {if (i > 0) cout << " ";  // 非首个元素前加空格cout << errors[i];}cout << endl;}// 输出获胜者（a>b则A胜，否则B胜）if (a > b) {cout << 0 << " " << a << endl;} else {cout << 1 << " " << b << endl;}return 0;
}