当前位置：首页 > news >正文

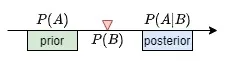
贝叶斯定理 vs 条件概率

news 2025/8/9 11:04:15

什么是贝叶斯定理，什么是条件概率？贝叶斯定理公式该如何记，如何理解？它在描述一个怎样的事实，有什么实际用途？让我们来重新认识贝叶斯定理，以及各种怎么也分不清的概率名称。

贝叶斯定理

对于独立随机事件，我们都知道多个独立随机事件发生的概率就等于各个随机事件发生概率的乘积，用公式来描述就是：

$\cap B)=P(A) \times P(B)$

比如抛两次骰子，第一次出现奇数(事件A)和第二次大于3(事件B)就是两个独立事件，第一次出现奇数且第二次大于3的概率就是两者概率的乘积： $\cap B)=0.5\times 0.5=0.25$ 。

这个公式虽然简单，但却是贝叶斯定理的基础，有了它，贝叶斯公式就水到渠成，甚至不用背诵也能轻松写出来，还不会写错。

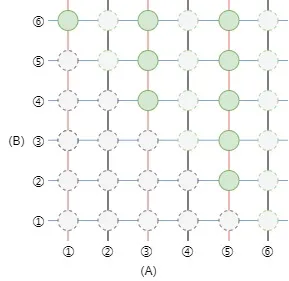
从古典概率的角度来看独立随机事件的联合概率是非常直观的。它相当于把样本空间和事件都做了一次全排列，也就是笛卡尔积。事实上我们也是这样计算联合概率的。

在这里插入图片描述

还是上面的例子，图中横向是事件A，纵向是事件B，绿色表示事件A和事件B同时发生的情况。然而当事件之间不再独立，而是互相影响，那么联合概率就不能简单的用事件单独发生的概率相乘来计算了。

虽然不能用事件独立发生的概率相乘来计算非独立事件的联合概率，但是公式并没有本质变化，依然是两个概率相乘，只不过现在变成了一个事件独立发生的概率乘以该事件发生的情况下另一个事件发生的概率。我们用 $P (B ∣ A)$ 来表示事件A已经发生的情况下，事件B发生的概率。那么事件A和事件B同时发生的概率就是：

$\cap B) = P(A) \times P(B|A)$

这个公式的结构还是两个事件概率的乘积，只不过后者是在前者发生条件下的概率。我们称 $P (B ∣ A)$ 为条件概率，即事件A发生的条件下，事件B发生的概率，它还是事件B的概率，只不过变成了条件概率。这一点是符合直觉的，并且在古典概率中，我们也是这样计算非独立事件的联合概率的。

很多地方会把公式写成 $P(A∩B)=P(B∣A)×P(A)P(A\cap B)=P(B|A)\times P(A)$ ，但是这样并不利于理解和记忆，因为它的阅读顺序违反了事件的发生顺序，条件概率必然发生在条件之后，这是事件的因果顺序。

在非独立事件中，我们不能再用全排列了，因为前面发生的事件会影响后面事件的样本空间，也就改变了后面事件的发生概率。比如我们把上面的例子改成第一次出现奇数(事件A)和两次点数之和大于6(事件B)，当我们再计算事件A和事件B的联合概率时，由于事件A的发生，事件B的样本空间也发生了改变，导致黑色竖线处的样本不可能再出现。即原本B的样本空间是36，当A发生后，就只剩18了。此时 $P(A∩B)=36×918=14P(A\cap B)=\frac{3}{6}\times\frac{9}{18}=\frac{1}{4}$ 。

在这里插入图片描述

事件本身是没有特异性的，事件A和事件B是等价的，它们没有任何区别，因此完全可以互换。我们将上面公式中的 $A$ 和 $B$ 互换，得到下面的公式：

$\cap B)=P(B) \times P(A|B)$

也就是事件A和事件B同时发生的概率也等于事件B发生的概率乘以事件B发生的条件下事件A发生的概率。事件发生的顺序不影响事件发生的概率，也不影响事件同时发生的概率，这也是贝叶斯定理成立的前提。既然结果都是 $P(A∩B)P(A\cap B)$ ，我们可以将两个等式联立一下：

$P(A\cap B)=P(A)\times P(B|A)=P(B)\times P(A|B)$

其实这就是贝叶斯公式了，我们常见的形式只是这个等式的变形。

$P(B|A)=\frac{P(B)\times P(A|B)}{P(A)}\tag{1}$

或者：

$P(A|B)=\frac{P(A)\times P(B|A)}{P(B)}\tag{2}$

比较常见的形式是后者，因为在贝叶斯公式中，每个概率都被赋予了不同的名称，比如第二种形式为例， $P (A)$ 叫做先验概率， $P (B ∣ A)$ 叫做似然度， $P (B)$ 叫做边际概率， $P (A ∣ B)$ 叫做后验概率。由于A和B是等价的，每种概率叫什么名字完全取决于它们在公式中的位置。本质上是根据一个已知条件(证据)去求一个事件个概率，事件本身的概率是先验概率，即没有任何证据佐证情况下的概率，而条件发生的概率就是边际概率。由于条件(证据)的出现改变了原本事件的发生概率，这个被求的条件概率就是后验概率，即有证据佐证后的概率。

这四个概率名称的翻译真是让人摸不着头脑，先验概率的“先验”原文是 prior，后验概率的“后验”原文是 posterior。它们本身只有前和后的意思，不管是原文还是译文都让人费解。
为什么叫先验？什么叫后验？没人能解释为什么，网上很多用因果来解释贝叶斯公式的，但是对于公式本身而言，事件A和事件B是没有任何差别的，凭什么A是因，B是果呢？所谓因果只是公式应用于具体问题而产生的意义，公式做为客观规律的抽象表述，是脱离于具体事物的，也就脱离了因果。
我能想到的最合理的推测是先验后验只是事情发展时间线上的位置关系的描述。以条件B的出现为界，往前事件B还未发生，此时事件A的概率就是 $P (A)$ ；往后事件B已经发生，此时事件A的概率也就变成了 $P (A ∣ B)$ 。

对于这两个单词我也没有更好的翻译，我只能说这个翻译很漂亮，但并不好理解，我也很难去考证贝叶斯本人原本的意思，至于“边际”的原文 marginal 和“似然”的原文 likelihood 就是直译而已。分清它们我们需要知道先验概率和后验概率描述的是同一个事件，而似然度和边际概率描述的是同一个事件。 $P (A ∣ B)$ 依然是事件A的概率，只是在事件B发生的前提下，它和 $P (A)$ 不再相等而已，但他们是对同一个事件的概率描述。

回到最原本的等式，我们给每一项都除以 $P(A)×P(B)P(A)\times P(B)$ 就能得到下面的等式：

$\frac{P(A\cap B)}{P(A)\times P(B)}=\frac{P(B|A)}{P(B)}=\frac{P(A|B)}{P(A)}$

等式中间是事件A发生的条件下事件B发生的概率与事件B单独发生概率的比值。由于事件A的出现改变了事件B发生的概率，这个比值可以看作是事件A对事件B出现的影响大小，即事件A的出现会使得事件B发生的概率提高或者降低百分之多少。同样，最右边的比值是事件B对事件A发生概率的影响。我们可以看到，事件A对事件B的影响和事件B对事件A的影响是一样大的，这个大小等于事件A和事件B的联合概率与事件A和事件B的概率之积的比值。下面是公式的图形表示：

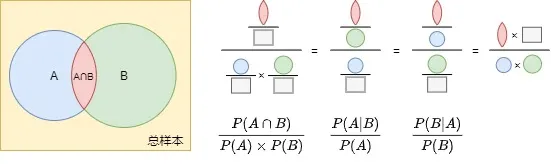
在这里插入图片描述

基于以上结论，那么贝叶斯公式其实还可以写成下面这样，我觉得这种形式是最容易理解和记忆的。

$P(A|B)=P(A)\times\frac{P(B|A)}{P(B)}$

它表示事件B的出现改变了事件A出现的概率，这个改变的比例是 $P(B∣A)P(B)\frac{P(B|A)}{P(B)}$ ，用它乘以事件A的概率，就是当我们观察到事件B时，事件A会发生的概率，无论这个概率是增大还是减小，我们都会对事件A的发生与否越来越确定。这就是贝叶斯公式的现实意义，通过观测证据更新事件的可信度，毕竟 50% 的概率对于决策是没有任何意义的，那还不如抛硬币。

假如条件C也和事件A有关系，并且事件C的出现会让事件A发生的概率改变 $P(C∣A)P(C)\frac{P(C|A)}{P(C)}$ ，如果事件B和事件C是相互独立的，那么根据独立随机事件的联合概率公式，我们很容易得到当事件B和C同时发生时，A发生的概率：

$P(A|\{B,C\})=P(A)\times\frac{P(B|A)}{P(B)}\times\frac{P(C|A)}{P(C)}$

推广到 $n$ 个条件也就是手到擒来，这就是我们改写公式形式的好处。但是要注意一个前提，那就是条件之间要是相互独立的，否则上面的公式是不成立的。这个公式常用于多特征分类，并且我们假定特征之间相互独立。

还有一种情况是事件B和事件C之间是独立的，但是当事件A存在时，事件B和事件C就不再独立。此时多条件的后验概率变为：

$P(A|\{B,C\})=P(A)\times\frac{P(B|A)}{P(B)}\times\frac{P(C|\{A,B\})}{P(C)}$

其实还是一样的格式，只是在算事件C对事件A的影响时，由于事件A的存在，事件B和事件C不再独立，因此需要考虑到事件B的影响。这个公式也可以推广到更多条件下。

给大家举个例子，还是上面掷骰子的例子，如果我们规定以下事件：

事件A：第一次出现奇数；
事件B：第二次出现偶数；
事件C：两次点数之和大于6；

此时如果要计算 $P(C|\{A,B\})$ ，就必须要用后面那个公式了，因为当事件C存在时，事件A和事件B是不独立的。举个例子，当点数之和大于6且第一次为1时，显然第二次只能是6点才能满足条件，2和4是取不到的。这也就是说，当事件C存在时，事件A的出现改变了事件B的样本空间，它们之间不再独立。感兴趣的朋友可以自己算一算。

示例一

做为牛马，每天早起上班的你要决定今天带不带伞。假设你所在的地区有一半的时候会下雨，另一半时间不下雨。某天早上你起床后看到天上有乌云，那么你是带伞呢还是不带呢？

平时出门都是抛一个硬币决定带不带伞，但是今天，凭直觉我们也知道应该带伞。那么我们该如何通过科学计算来验证呢？

前面我们知道了下雨和不下雨的概率各占50%，要计算今天下雨的概率，我们还需要掌握另一个信息。即不下雨的时候，有30%的时候有云，也就是有30%是阴天，而下雨的时候90%的情况有云。现在，我们知道了以下概率：

$\begin{matrix}P(晴)=0.5 & P(云|晴)=0.3\\ P(雨)=0.5 & P(云|雨)=0.9\end{matrix}$

现在我们要计算的是 $P (雨 ∣ 云)$ ，直接上公式：

$\begin{aligned}P(雨|云)&=\frac{P(雨)\times p(云|雨)}{P(云)}=\frac{P(雨)\times p(云|雨)}{P(晴)\times P(云|晴)+P(雨)\times P(雨|云)}\\&=\frac{0.5\times0.9}{0.5\times0.3+0.5\times0.9}=\frac{0.9}{1.2}=0.75\end{aligned}$

这里求 $P (云)$ 用到的 $P(晴)×P(云∣晴)+P(雨)×P(雨∣云)P(晴)\times P(云|晴)+P(雨)\times P(雨|云)$ 就是所谓的全概率公式，即：

$P(B)=\sum_{i=1}^n P(A_i)\times P(B|A_i)$

根据贝叶斯公式，我们计算出了今天下雨的概率是75%，所以出门的时候还是把伞带上吧。当然，如果你有大头的话，也可以不用带。大头大头，下雨不愁，人有雨伞，我有大头！

示例二

当你带着雨伞到达公司，你接到了一项给细菌分类的任务，老板给了你一批细菌样本，要求你分析细菌特征和致病性，并对是否致病做出分类，并且能预测新细菌是否致病。

经过研究你发现，这些细菌会合成不同形状的蛋白质，有圆形，三角形，方形和星形，它们有的厌氧，有的好氧，有的有菌毛，有的很光滑。于是你决定就用这些特征来对它们进行统计分析。下面是你得到的统计结果。

致病性		蛋白质		呼吸方式		菌毛
致病	80%	◯	20%	有氧呼吸	65%	有	72%
		∆	18%	有氧呼吸	65%	有	72%
		▢	10%	无氧呼吸	35%	无	28%
		☆	52%	无氧呼吸	35%	无	28%
不致病	20%	◯	4%	有氧呼吸	80%	有	40%
		∆	64%	有氧呼吸	80%	有	40%
		▢	20%	无氧呼吸	20%	无	60%
		☆	12%	无氧呼吸	20%	无	60%