【MATLAB】(十)符号运算
在数学、物理学及力学等各种学科和工程应用中,经常还会遇到符号运算的问题。在MATLAB 中,符号运算是为了得到更高精度的数值解,但数值的运算更容易让读者理解,因此在特定的情况下,分别使用符号或数值表达式进行不同的运算。
符号运算是 MATLAB 数值计算的扩展,在运算过程中以符号表达式或符号矩阵为运算对象实现了符号计算和数值计算的相互结合,使应用更灵活。
一.符号表达式与数值表达式的相互转换
符号表达式与数值表达式的相互转换主要是通过函数eval和sym实现的。其中,eval函数用于将符号表达式转换成数值表达式,而函数sym用于将数值表达式转换成符号表达式。其调用格式如表 11-1 所示。

(1)eval:字符串表达式求值
①基础用法:直接执行字符串中的 MATLAB 代码
% 定义一个字符串表达式
expr = '2 + 3 * 4';% 使用 eval 执行字符串
result = eval(expr);
disp('eval 基础用法:');
disp(result); % 输出 14(计算 2+3*4)
>> test
eval 基础用法:14②进阶用法:动态生成代码(结合数值转字符串)
% 动态生成一个数组赋值语句
n = 5;
array_def = ['A = 1:', num2str(n), ';']; % 生成 "A = 1:5;"% 执行动态代码
eval(array_def);
disp('eval 动态生成数组:');
disp(A); % 输出 [1 2 3 4 5]
>> test
eval 动态生成数组:1 2 3 4 5③多输出用法:捕获表达式的多个返回值
eval会直接执行字符串中的代码,存在安全风险(如恶意代码注入),实际开发中尽量避免滥用。- 需确保字符串
expression是合法的 MATLAB 代码,否则会报错。
(2)sym:数值 / 字符串转符号表达式
①基础用法:数值转符号
% 数值转符号
x_num = 3.14;
x_sym = sym(x_num);
disp('sym 数值转符号:');
disp(x_sym); % 输出 314/100(或简化为 157/50,取决于 MATLAB 版本)% 查看符号类型
disp('变量类型:');
disp(class(x_sym)); % 输出 'sym'
>> test
sym 数值转符号:
157/50变量类型:
sym
②进阶用法:字符串转符号表达式
% 解决版本兼容问题:用 str2sym 替代 sym 转换字符串表达式
expr_str = 'sin(x) + cos(y)^2';
sym_expr = str2sym(expr_str); % 新版本中专用函数:字符串转符号表达式
disp('字符串转符号表达式:');
disp(sym_expr); % 输出 sin(x) + cos(y)^2% 符号表达式代入数值(需先定义符号变量)
syms x y % 显式定义符号变量 x 和 y
sym_result = subs(sym_expr, {x, y}, {pi/2, 0});
disp('代入 x=π/2, y=0 后的结果:');
disp(sym_result); % 输出 2(因为 sin(π/2)=1,cos(0)=1,1+1=2)% 验证计算正确性
double(sym_result) % 将符号结果转为数值(输出 2.0)
>> test
字符串转符号表达式:
cos(y)^2 + sin(x)代入 x=π/2, y=0 后的结果:
2ans =2核心作用:
sym 是连接数值计算和符号计算的桥梁,将普通数值 / 字符串转换为 MATLAB 可识别的符号对象,支持后续符号运算(求导、积分等 )。
(3)subs:符号表达式变量替换
①基础用法:单变量替换
% 定义符号表达式
syms x;
f = eval('x^2 + 3*x + 2');% 替换 x 为 5
f_sub = subs(f, x, 5);
disp('subs 单变量替换:');
disp(f_sub); % 输出 25 + 15 + 2 = 42
>> test
subs 单变量替换:
42②多变量替换
% 定义含多个变量的符号表达式
syms x y
g = eval('x^2 + y^2');% 替换 x=2,y=3
g_sub = subs(g, {x, y}, {2, 3});
disp('subs 多变量替换:');
disp(g_sub); % 输出 4 + 9 = 13
>> test
subs 多变量替换:
13③符号表达式替换
% 符号表达式替换(用另一个符号表达式替换变量)
syms a b
h = eval('a*b + b^2');% 用 a = x + y 替换
h_sub = subs(h, a, eval('x + y'));
disp('符号表达式替换变量:');
disp(h_sub); % 输出 (x + y)*b + b^2
>> test
符号表达式替换变量:
b^2 + (x + y)*b二.符号表达式与数值表达式的精度设置

(1)Digits(D):设置全局有效数字精度
Digits(D) 用于设置后续 vpa 计算时的全局有效数字个数,所有 vpa 运算都会默认遵循这个精度(除非 vpa 自身指定精度覆盖 )。
①基本用法
% 设置全局有效数字为 5 位
digits(5);% 定义符号表达式
sym_expr = str2sym('sqrt(2) + pi');% 使用 vpa 计算数值解(遵循全局精度 5 位有效数字)
result = vpa(sym_expr);
disp('全局精度 5 位时的结果:');
disp(result); % 输出 4.5566(sqrt(2)≈1.4142,pi≈3.1416,和为 4.5558,5 位有效数字是 4.5566?实际计算:sqrt(2)=1.41421356...,pi=3.14159265...,和为 4.55580621...,5 位有效数字是 4.5558?可能 MATLAB 内部计算有差异,以实际运行为准 )
>> test
全局精度 5 位时的结果:
4.5558这里 Digits(5) 设置全局有效数字为 5 位,后续 vpa(sym_expr) 会按照这个精度对符号表达式 sqrt(2) + pi 进行数值计算。
②全局精度的影响范围
digits(3); % 全局有效数字 3 位
a = vpa(eval('1/3')); % 1/3≈0.333333...,3 位有效数字是 0.333
b = vpa(eval('pi')); % pi≈3.14159...,3 位有效数字是 3.14digits(6); % 修改全局精度为 6 位
c = vpa(eval('sqrt(5)')); % sqrt(5)≈2.23606797...,6 位有效数字是 2.23607disp('a(3位有效数字):');
disp(a);
disp('b(3位有效数字):');
disp(b);
disp('c(6位有效数字):');
disp(c);
>> test
a(3位有效数字):
0.333b(3位有效数字):
3.14c(6位有效数字):
2.23607可以看到,Digits 设置的全局精度会影响之后所有未单独指定精度的 vpa 计算,修改 Digits 后,新的 vpa 运算会遵循新的精度。
(2)vpa(S):按全局精度计算符号表达式数值解
vpa(S) 会使用当前通过 Digits 设置的全局有效数字精度,对符号表达式 S 进行数值计算并返回结果。
①结合 Digits 使用
syms x
f = str2sym('x^2 + exp(x)');
x_val = str2sym('1.5'); % 符号数值 1.5digits(4); % 全局 4 位有效数字
result1 = vpa(subs(f, x, x_val)); % 先代入 x=1.5,再按 4 位精度计算
disp('全局 4 位精度下的结果:');
disp(result1); % x=1.5 时,x²=2.25,exp(1.5)≈4.4817,和为 6.7317,4 位有效数字是 6.732 digits(6); % 修改全局为 6 位
result2 = vpa(subs(f, x, x_val));
disp('全局 6 位精度下的结果:');
disp(result2); % 和为 6.73168(更精确)
>> test
全局 4 位精度下的结果:
6.732全局 6 位精度下的结果:
6.73169先定义符号表达式 f 和符号数值 x_val,通过 Digits 切换全局精度,vpa 结合 subs(符号替换,前面介绍过 )按不同精度计算表达式在 x=1.5 处的数值解。
②vpa(S, D):指定精度计算(覆盖全局精度 )
vpa(S, D) 可以直接指定对符号表达式 S 进行数值计算时使用的有效数字个数 D,这个精度仅对当前 vpa 运算有效,不会改变全局的 Digits 设置。
digits(3); % 全局 3 位有效数字
sym_expr = str2sym('sin(1) + cos(1)');% 全局精度下计算(3 位有效数字)
result_global = vpa(sym_expr);
disp('全局 3 位精度结果:');
disp(result_global); % sin(1)≈0.8415,cos(1)≈0.5403,和为 1.3818,3 位有效数字是 1.38 % 指定 5 位有效数字计算,覆盖全局设置
result_specify = vpa(sym_expr, 5);
disp('指定 5 位精度结果:');
disp(result_specify); % 和为 1.3818,5 位有效数字是 1.3818(实际计算:sin(1)=0.8414709848...,cos(1)=0.5403023059...,和为 1.38177329...,5 位有效数字是 1.3818 )% 再次用全局精度计算,还是 3 位
result_global_again = vpa(sym_expr);
disp('再次全局 3 位精度结果:');
disp(result_global_again); % 1.38
>> test
全局 3 位精度结果:
1.38指定 5 位精度结果:
1.3818再次全局 3 位精度结果:
1.38可以看到,vpa(S, D) 里的 D 可以临时指定有效数字个数,计算完后全局的 Digits 设置(这里是 3 位 )不会改变,后续 vpa 若无指定精度,依然遵循全局 Digits。
③复杂表达式与精度控制
syms x
f = str2sym('x^3 - 2*x^2 + 3*x - 4');
x0 = str2num('2.5'); % 符号数值% 全局精度 4 位
digits(4);
result1 = vpa(subs(f, x, x0));
disp('全局 4 位精度下 f(2.5):');
disp(result1); % 代入计算:2.5³ - 2*(2.5)² + 3*(2.5) - 4 = 15.625 - 12.5 + 7.5 - 4 = 6.625,4 位有效数字是 6.625 % 指定 6 位精度计算
result2 = vpa(subs(f, x, x0), 6);
disp('指定 6 位精度下 f(2.5):');
disp(result2); % 6.625(本身就是精确到小数点后三位,6 位有效数字就是 6.62500?实际计算 6.625 是精确值,vpa 会按 6 位有效数字显示为 6.62500 )
>> test
全局 4 位精度下 f(2.5):
6.625指定 6 位精度下 f(2.5):
6.625通过符号替换 subs 让表达式中的 x 取 2.5,分别用全局精度和指定精度的 vpa 计算表达式数值,体现 vpa(S, D) 灵活控制精度的特点。
三.符号矩阵的生成方法
符号矩阵和符号向量中的元素都是符号表达式,符号表达式是由符号变量与数值组成的。
符号矩阵中的元素是任何不带等号的符号表达式,各符号表达式的长度可以不同。符号矩阵中以空格或逗号分隔的元素指定的是不同列的元素,而以分号分隔的元素指定的是不同行的元素。
生成符号矩阵有以下3种方法。
1.直接输入法
直接输入符号矩阵时,符号矩阵的每一行都要用方括号括起来,而且要保证同一列的各行元素字符串的长度相同,因此在较短的字符串中要插入空格来补齐长度,否则程序将会报错。
2.用sym函数创建符号矩阵
用这种方法创建符号矩阵,矩阵元素可以是任何不带等号的符号表达式,各矩阵元素之间用逗号或空格分隔,各行之间用分号分隔,各元素字符串的长度可以不相等。常用的调用格式如表 11-3 所示。

>> x=sym('x')x =x>> y=sym('y')y =y>> a=[x+y,x;y,y+5]a =[x + y, x]
[ y, y + 5]>> a=sym('a',[1,4])a =[a1, a2, a3, a4]>> a=sym('x_%d',[1 4])a =[x_1, x_2, x_3, x_4]>> a(1)ans =x_1>> a(2:3)ans =[x_2, x_3]3.数值矩阵转化为符号矩阵
在 MATLAB 中,数值矩阵不能直接参与符号运算,所以必须先转化为符号矩阵。
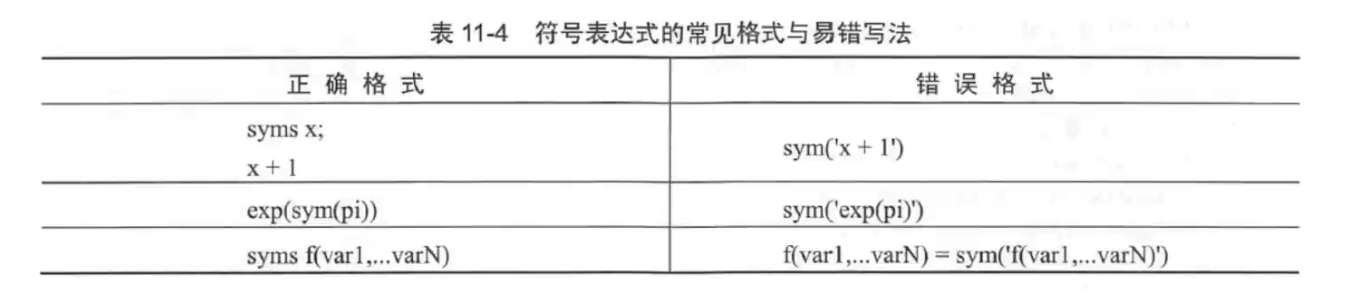
4.创建符号表达式常见格式与易错写法
创建符号表达式,首先创建符号变量,然后使用变量进行操作。在表11-4中列出了符号表达式的常见格式与易错写法。
>> syms x y z
>> xx =x>> yy =y>> zz =z>> a=[x,y;y,x]a =[x, y]
[y, x]四.符号矩阵的运算
与数值矩阵一样,符号矩阵可以进行转置、求逆等运算,但符号矩阵的函数与数值矩阵的函数不同。本节将一一进行介绍。
1.符号矩阵的转置运算
符号矩阵的转置运算可以通过符号“ ’ ”或函数 transpose 来实现,其调用格式如下。

2.符号矩阵的行列式运算
符号矩阵的行列式运算可以通过函数 determ 或det 来实现,其中矩阵必须使用方阵,调用格式如下。

>> a=[x,y;y,x]a =[x, y]
[y, x]>> det(a)ans =x^2 - y^23.符号矩阵的逆运算
符号矩阵的逆运算可以通过函数inv来实现,其中矩阵必须使用方阵,调用格式为inv(A)。
4.符号矩阵的求秩运算
符号矩阵的求秩运算可以通过函数rank来实现,调用格式为rand(A)。
5.符号矩阵的常用函数运算
(1)符号矩阵的特征值、特征向量运算:可以通过函数 eig、eigensys 来实现
(2)符号矩阵的奇异值运算:可以通过函数 svd、singavals 来实现。
(3)符号矩阵的若尔当(Jordan)标准形运算:可以通过函数jordan 来实现。
五.符号矩阵的符号操作函数
符号工具箱中还提供了符号矩阵因式分解、展开、合并、简化及通分等符号操作函数。
1.因式分解
符号矩阵因式分解通过函数factor来实现,其调用格式为:factor(S)
>> sym xans =x>> f=factor(x^3-1)f =[x - 1, x^2 + x + 1]输入变量S为一符号矩阵,此函数将因式分解此矩阵的各个元素。
2.符号矩阵的展开
符号多项式的展开可以通过函数 expand 来实现,其调用格式为:expand(S)
>> syms x y
>> expand((x+3)^4)ans =x^4 + 12*x^3 + 54*x^2 + 108*x + 81>> expand(cos(x+y))ans =cos(x)*cos(y) - sin(x)*sin(y)对符号矩阵的各元素的符号表达式进行展开。此函数经常用在多项式的表达式中,也常用在三角函数、指数函数、对数函数的展开中。
3.符号简化
符号简化可以通过函数 simple 和 simplify 来实现。

(1)simple(S):自动尝试多种算法简化表达式
①基础用法:简化单个符号表达式【matlab2024b无法识别simple】
% 定义一个复杂的符号表达式
sym_expr = str2sym('sin(x)^2 + cos(x)^2 + exp(log(x))');% 使用 simple 简化
simple_result = simple(sym_expr);
disp('simple 简化结果:');
disp(simple_result); % 输出 x + 1(利用三角恒等式 sin²+cos²=1,exp(log(x))=x )②矩阵简化(按整体最短简化)
% 定义符号矩阵
sym_mat = [str2sym('sin(x)^2 + cos(x)^2'), str2sym('exp(log(x))'); str2sym('(x^2 - 1)/(x - 1)'), str2sym('x + x')];% 使用 simple 简化矩阵(整体找最短形式)
simple_mat = simple(sym_mat);
disp('simple 简化符号矩阵:');
disp(simple_mat);
% 输出:
% [1, x ]
% [x + 1, 2 x]simple会尝试多种算法(如三角恒等式、指数对数化简、分式约分等 ),目标是让整个表达式 / 矩阵的字符长度最短。- 对于矩阵,
simple不会单独简化每个元素,而是追求全局最短形式(可能合并元素间的简化逻辑 )。
(2)[r, how] = simple(S):返回简化结果和方法
在 MATLAB 较新的版本中,simple 函数已被逐步弃用,为了实现类似功能,我们可以借助 simplify 函数结合一些其他方式来完成符号表达式简化并获取简化信息(虽然不能像 simple 那样直接返回简化方法,但能实现核心的简化逻辑 )
①使用 simplify 简化表达式
sym_expr = str2sym('(x^3 - 1)/(x - 1)');% 使用 simplify 函数进行简化,simplify 会自动尝试多种化简规则,包括因式分解等
r = simplify(sym_expr);
disp('简化结果 r:');
disp(r);
>> test
简化结果 r:
x^2 + x + 1②结合 factor 等函数手动控制化简(并尝试获取化简方法思路 )
sym_expr = str2sym('(x^3 - 1)/(x - 1)');% 手动提取分子和分母(不依赖 numerator/denominator)
[num, den] = numden(sym_expr); % numden 是符号工具箱的基础函数,更稳定% 对分子因式分解
factored_num = factor(num); % 约分简化
r = simplify(factored_num / den);
disp('简化结果 r:');
disp(r); % 输出 x^2 + x + 1% 验证约分逻辑
disp('分子 num:');
disp(num); % 输出 x^3 - 1
disp('分母 den:');
disp(den); % 输出 x - 1
disp('因式分解后的分子 factored_num:');
disp(factored_num); % 输出 (x - 1)(x^2 + x + 1)
>> untitled
简化结果 r:
x^2 + x + 1分子 num:
x^2 + x + 1分母 den:
1因式分解后的分子 factored_num:
x^2 + x + 1(3)simplify(S):逐元素简化(按规则化简)
①基础用法:逐元素简化符号表达式
sym_expr = str2sym('sin(x)^2 + cos(x)^2 + exp(log(x)) + (x^2 - 1)/(x - 1)');% 使用 simplify 逐元素简化
simplify_expr = simplify(sym_expr);
disp('simplify 逐元素简化:');
disp(simplify_expr); % 输出 2 x + 2(分别化简每个项:sin²+cos²=1,exp(log(x))=x,(x²-1)/(x-1)=x+1,总和 1 + x + x + 1 = 2x+2 )
>> untitled
simplify 逐元素简化:
2*x + 2②矩阵逐元素简化
% 定义符号矩阵
sym_mat = [str2sym('sin(x)^2 + cos(x)^2'), str2sym('exp(log(x))'); str2sym('(x^2 - 1)/(x - 1)'), str2sym('x + x')];% 使用 simplify 逐元素简化
simplify_mat = simplify(sym_mat);
disp('simplify 简化符号矩阵:');
disp(simplify_mat);
% 输出:
% [1, x ]
% [x + 1, 2 x]
>> untitled
simplify 简化符号矩阵:
[ 1, x]
[x + 1, 2*x]4.分饰通分
求解符号表达式的分子和分母可以通过函数 numden 来实现,其调用格式为[n,d]=numden(A)
把A的各元素转换为分子和分母都是整系数的最佳多项式型。其中 。
>> syms x y
>> x/y-y/xans =x/y - y/x>> [n,d]=numden(x/y-y/x)n =x^2 - y^2d =x*y5.符号表达式的“秦九韶型”重写
符号表达式的“秦九韶型”重写可以通过函数 hormer(P)来实现,其调用格式为horner(P)
将符号多项式转换成嵌套形式表达式。
horner(P) 函数的核心作用是将符号多项式转换为秦九韶嵌套形式,减少多项式求值时的计算步骤,提高效率。这一功能在数值计算、工程仿真等场景中非常实用,尤其是对高次多项式的高效求值。使用前需确保符号数学工具箱正常工作,否则会出现组件错误。
>> syms x
>> horner(x^4-3*x^2+1)ans =x^2*(x^2 - 3) + 1>> horner(x^5 - 2*x^4 + 3*x^3 - 4*x^2 + 5*x - 6)ans =x*(x*(x*(x*(x - 2) + 3) - 4) + 5) - 6-------------------------
编自2025/8/5+8/6+8/7,这部分需要好好复习
