当前位置：首页 > news >正文

「日拱一码」045 机器学习-因果发现算法

news 2025/8/8 12:18:11

基于约束的方法 (Constraint-based)

基于评分的方法 (Score-based)

基于函数因果模型的方法 (Functional Causal Models)

基于梯度的方法 (Gradient-based)

因果发现是机器学习中一个重要的研究方向，它旨在从观测数据中推断变量之间的因果关系

基于约束的方法 (Constraint-based)

核心思想：利用条件独立性检验来推断因果结构
代表算法：PC算法、FCI算法、RFCI算法

## 因果发现算法
# 1. 基于约束的方法——PC算法
from pgmpy.estimators import PC
import pandas as pd
import numpy as np# 生成数据
data = pd.DataFrame(np.random.randn(1000, 3), columns=['X', 'Y', 'Z'])# PC算法
est = PC(data)
model = est.estimate(variant="orig", alpha=0.05)  
print("因果边:", model.edges())

基于评分的方法 (Score-based)

核心思想：定义评分函数评估图结构，搜索得分最高的图
代表算法：GES算法、FGES算法

# 2. 基于评分的方法——GES算法
import numpy as np
import pandas as pd
import networkx as nx
import matplotlib.pyplot as plt
from itertools import permutations
from sklearn.linear_model import LinearRegressionnp.random.seed(42)
X = np.random.normal(size=1000)
Y = 0.5 * X + np.random.normal(size=1000)
Z = 0.3 * Y + np.random.normal(size=1000)
data = pd.DataFrame({'X': X, 'Y': Y, 'Z': Z})variables = data.columns.tolist()  
print("变量列表:", variables)  # ['X', 'Y', 'Z']def compute_bic(data, parents_dict):"""计算 BIC 评分（线性高斯模型）"""score = 0for node in data.columns:X = data[parents_dict[node]] if parents_dict[node] else np.zeros((len(data), 1))y = data[node]model = LinearRegression().fit(X, y)residuals = y - model.predict(X)n = len(data)k = len(parents_dict[node])sigma2 = np.var(residuals)score += -n * np.log(sigma2) / 2 - k * np.log(n) / 2return score# 穷举所有可能的 DAG（检查 edges 生成）
best_score = -np.inf
best_graph = Noneall_edges = list(permutations(variables, 2))
print("所有可能的边组合:", all_edges)  # [('X', 'Y'), ('X', 'Z'), ('Y', 'X'), ('Y', 'Z'), ('Z', 'X'), ('Z', 'Y')]for u, v in all_edges:graph = {node: [] for node in variables}graph[v].append(u)  # 添加边 u -> vscore = compute_bic(data, graph)if score > best_score:best_score = scorebest_graph = graph# 可视化
G = nx.DiGraph()
for node in best_graph:for parent in best_graph[node]:G.add_edge(parent, node)nx.draw(G, with_labels=True, node_color='lightgreen')
plt.title("GES Algorithm (Simplified)")
plt.savefig('ges_graph.png')
plt.show()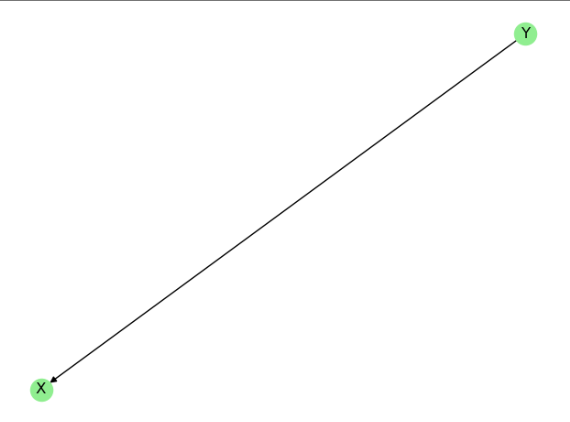

基于函数因果模型的方法 (Functional Causal Models)

核心思想：假设数据生成过程的函数形式
代表算法：LiNGAM、ANM（加性噪声模型）、PNL（后非线性模型）

# 3. 基于函数因果模型的方法——LiNGAM
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import networkx as nx
from itertools import permutationsnp.random.seed(42)
X = np.random.normal(size=1000)
Y = 0.5 * X + np.random.normal(size=1000)
Z = 0.3 * Y + np.random.normal(size=1000)
data = pd.DataFrame({'X': X, 'Y': Y, 'Z': Z})data = (data - data.mean()) / data.std()try:# 尝试使用 causallearn 的 LiNGAMfrom causallearn.search.FCMBased.lingam import DirectLiNGAMmodel = DirectLiNGAM()model.fit(data)adj_matrix = model.adjacency_matrix_print("LiNGAM 邻接矩阵:\n", adj_matrix)# [[0.         0.41099056 0.]#  [0.         0.         0.]# [0.          0.31428138 0.]]except ImportError:print("未找到 causallearn，改用简化版 LiNGAM（基于回归残差）")# 简化版 LiNGAM（基于残差独立性检验）adj_matrix = np.zeros((3, 3))  # 初始化邻接矩阵variables = data.columns.tolist()for i, target in enumerate(variables):predictors = [var for var in variables if var != target]X_pred = data[predictors].valuesy_target = data[target].values# 多元线性回归coef = np.linalg.lstsq(X_pred, y_target, rcond=None)[0]residuals = y_target - X_pred.dot(coef)# 检查残差与预测变量的独立性（简化版：相关系数）for j, predictor in enumerate(predictors):corr = np.corrcoef(residuals, data[predictor])[0, 1]if abs(corr) < 0.05:  # 阈值可调整adj_matrix[variables.index(predictor), i] = 1  # predictor -> target# 可视化
G = nx.DiGraph(adj_matrix)
pos = nx.spring_layout(G)
nx.draw(G, pos, with_labels=True, node_size=1000, arrowsize=20,node_color='lightgreen', edge_color='gray')
plt.title('LiNGAM Causal Graph (Direct)' if 'model' in locals() else 'Simplified LiNGAM')
plt.show()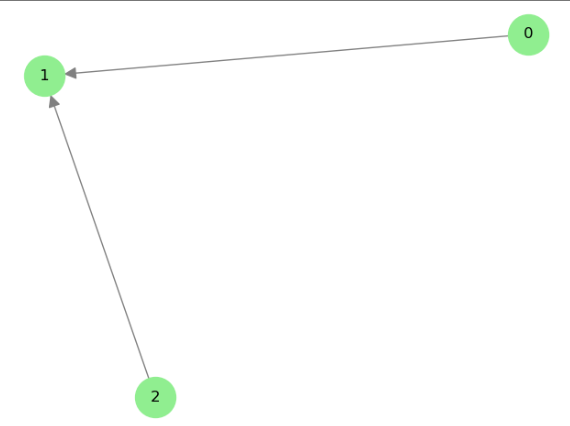

基于梯度的方法 (Gradient-based)

核心思想：使用神经网络和梯度下降学习因果结构
代表算法：DAG-GNN、NOTEARS

# 4. 基于梯度的方法——NOTEARS
import numpy as np
import networkx as nx
import matplotlib.pyplot as plt# 生成数据
np.random.seed(42)
X = np.random.normal(size=1000)
Y = 0.5 * X + np.random.normal(size=1000)
Z = 0.3 * Y + np.random.normal(size=1000)
data = np.column_stack([X, Y, Z])
data = (data - data.mean(axis=0)) / data.std(axis=0)  # 标准化# 自定义简化版NOTEARS（梯度下降优化）
def notears_simple(X, lambda1=0.1, max_iter=100):n_features = X.shape[1]W = np.zeros((n_features, n_features))  # 初始化邻接矩阵for _ in range(max_iter):# 计算梯度（最小二乘损失 + 无环约束）grad = -X.T @ (X - X @ W) / len(X) + lambda1 * np.sign(W)# 投影梯度更新（确保无环）W -= 0.01 * grad  # 学习率W = np.clip(W, -1, 1)  # 限制权重范围return (W != 0).astype(int)  # 二值化邻接矩阵# 运行并可视化
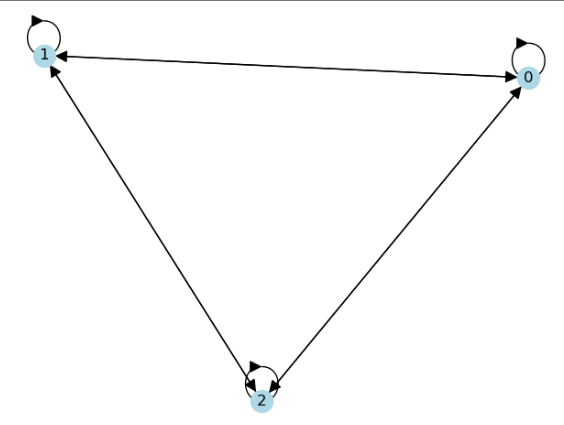
W_est = notears_simple(data)
labels = ['X', 'Y', 'Z']
G = nx.DiGraph(W_est, labels=labels)
nx.draw(G, with_labels=True, node_color='lightblue', arrowsize=20)
plt.title('Simplified NOTEARS Result')
plt.show()