优选算法 力扣 LCR 179. 查找总价格为目标值的两个商品 双指针降低时间复杂度 C++题解 每日一题

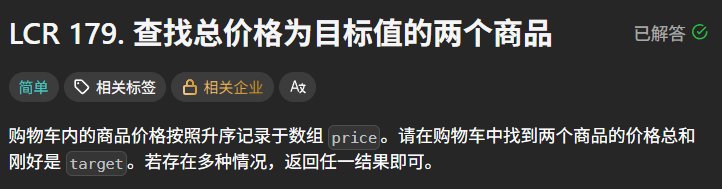
零、题目描述

题目链接：查找总价格为目标值的两个商品

题目描述：

示例 1：
输入：price = [3, 9, 12, 15], target = 18
输出：[3, 15] 或 [15, 3]

示例 2：
输入：price = [8, 21, 27, 34, 52, 66], target = 61
输出：[27, 34] 或 [34, 27]

提示：
1 <= price.length <= 10^5
1 <= price[i] <= 10^6
题目数据保证存在至少一组有效答案

一、为什么这道题值得你花几分钟看懂？

查找总价格为目标值的两个商品问题，是双指针算法在“有序数组搜索”中的典型应用。它的核心价值在于：让你掌握如何利用数组的有序性，将搜索复杂度从 O(n²) 降至 O(n)，并理解细节优化对算法效率的决定性影响。

这道题的巧妙之处在于：

• 数组的升序特性为双指针提供了“移动单调性”基础——左移右指针必然减小总和，右移左指针必然增大总和
• 看似简单的“找到答案后立即退出”操作（即你踩坑的break），直接决定了算法能否通过时间限制

搞定这道题，你会掌握：

• 双指针在“首尾夹击”场景中的核心逻辑
• 如何利用数组有序性避免无效搜索
• 边界细节（如提前退出）对大规模数据场景的性能影响

这种“用指针代替枚举，用顺序优化搜索”的思路，是解决有序数组问题的核心方法论。

二、从超时到通关：思路的优化路径

1. 暴力枚举：必超时的尝试

最直观的思路是枚举所有两数组合，判断和是否等于目标值：

暴力解法思路：

// 伪代码
for (int i = 0; i < n; i++) {for (int j = i + 1; j < n; j++) {if (price[i] + price[j] == target) {return {price[i], price[j]};}}
}

问题分析：

• 时间复杂度：O(n²)，当 n=10⁵ 时，运算次数高达 10¹⁰，远超时间限制
• 核心缺陷：完全无视数组的有序性，进行无意义的重复计算

2. 双指针初版：未优化的隐患

受有序数组特性启发，可使用双指针缩小搜索范围，但初版可能忽略关键优化：

未加break的双指针思路：

// 伪代码（存在超时风险）
int left = 0, right = n-1;
while (left < right) {if (sum > target) right--;else if (sum < target) left++;else {// 找到答案但未退出，继续循环到left >= rightres = {price[left], price[right]};}
}
return res;

问题分析：

• 虽然指针移动逻辑正确，但找到答案后仍继续循环，导致 O(n) 的无效操作
• 当 n=10⁵ 时，这部分多余操作足以触发超时（这正是你遇到的问题）

3. 双指针优化版：break的关键作用

在找到有效解后立即退出循环，避免无效计算：

优化核心：

• 题目明确“存在至少一组有效答案”，因此无需搜索全部解
• 找到第一组解后，break 可终止后续无意义的指针移动

这一细节将实际运行时间从 O(n) 降至远小于 n 的水平，完美适配大规模数据。

三、双指针实现：首尾夹击，一击即中

1. 算法步骤

1. 初始化双指针：left = 0（数组起点），right = price.size() - 1（数组终点）
2. 循环搜索（left < right）：
   • 计算当前和 sum = price[left] + price[right]
   • 若 sum > target：右指针左移（right--），减小总和
   • 若 sum < target：左指针右移（left++），增大总和
   • 若 sum == target：记录结果并立即break（终止循环）
3. 返回找到的两个价格

2. 代码实现（优化版）

class Solution {
public:vector<int> twoSum(vector<int>& price, int target) {int left = 0, right = price.size() - 1;vector<int> a(2);  // 存储结果while (left < right) {if (price[left] + price[right] > target) {right--;  // 总和过大，右指针左移减小总和} else if (price[left] + price[right] < target) {left++;   // 总和过小，左指针右移增大总和} else {// 找到目标组合，记录结果并退出循环a[0] = price[left];a[1] = price[right];break;  // 关键优化：避免后续无效循环}}return a;}
};

四、代码解析与超时原因深度分析

1. 示例走读（示例2：price = [8,21,27,34,52,66], target = 61）

• 初始：left=0（8），right=5（66），和=74 > 61 → right=4（52）
• 和=8+52=60 < 61 → left=1（21）
• 和=21+52=73 > 61 → right=3（34）
• 和=21+34=55 < 61 → left=2（27）
• 和=27+34=61 == 61 → 记录 [27,34] 并 break
• 循环终止，返回结果。全程仅5次判断，效率极高

2. 为什么缺少break会超时？

• 时间对比：
  • 有break：找到答案后立即退出，实际操作次数通常远小于 n（如示例仅5次）
  • 无break：必须遍历到 left >= right，即使找到答案仍需执行 O(n) 次操作
• 数据规模影响：当 n=10⁵ 时，无break版本需执行约 10⁵ 次判断，而有break版本可能仅需几十次，差距达数千倍

3. 复杂度分析

复杂度类型	具体值	说明
时间复杂度	O(n)	最坏情况遍历一次数组，实际因break远低于n
空间复杂度	O(1)	仅使用常数变量，无需额外存储空间

相比哈希表解法（O(n) 空间），双指针在空间效率上更优，是有序数组场景的最优解。

五、常见问题与注意事项

1. 双指针为什么能正确找到解？

数组的有序性保证了指针移动的单调性：

• 若当前和过大，只有左移右指针能减小总和（因右侧元素更大）
• 若当前和过小，只有右移左指针能增大总和（因左侧元素更小）
• 这种“不回头”的移动方式，确保不会遗漏有效解

2. 数组中存在重复元素会影响结果吗？

不会。题目允许返回任意一组解，重复元素不改变指针移动逻辑：

• 例如 price = [2,2,3], target=4，双指针会找到 [2,2] 并正确返回

3. 为什么不需要考虑 left <= right 的边界？

循环条件 left < right 确保了两指针指向不同元素，符合“两个商品”的题意，且避免了重复计算同一元素的情况。

六、举一反三

这道题的“首尾双指针 + 提前退出”思路可推广到：

• 有序数组的两数问题：如两数之差为目标值、两数乘积为目标值等
• 优化搜索效率的场景：如在找到唯一解后立即终止遍历

下一题预告：LeetCode 15. 三数之和！这道题是双指针的进阶挑战，需要在“两数之和”基础上增加一层循环，同时处理重复解的去重问题。你将学到如何在固定一个元素后，用双指针寻找另外两个元素，并用巧妙的去重逻辑避免重复结果，进一步深化对双指针的理解。

最后欢迎在评论区分享你对“break”优化的感悟，或探讨其他解题思路～ 若有更精妙的想法，期待你的指点！😊

✨ 如果你觉得这篇解析有帮助，不妨：

• 🌟 点个赞，让更多人看到这份实用思路
• ⭐ 收个藏，下次遇到类似问题能快速复习
• 👀 加个关注，明天的三数之和解析更精彩

这是封面原图，算法的优化往往藏在细节里，咱们明天见！😉