01数据结构-哈夫曼树

1.哈夫曼树

1.1哈夫曼树相关的几个名词

• 路径：在一棵树中，一个节点到另一个节点的通路，称为路径。例如：从根节点到节点a之间的通路就是一条路径
• 路径长度：在一条路径中，每经过一个节点，路径长度都要加1。例如：规定根节点所在层数为1层，那么从根节点到第i层节点的路径长度为i-1
• 节点的权：给每一个节点赋予一个新的数值，被称为这个节点的权，例如节点a的权为7，节点b的权为5.
• 节点的带权路径长：指的是从根节点到该节点之间的路径长度与该节点的权的乘积。例如：节点b的带权路径长度为2+5=10。树的带权路径长度为树中所有叶子节点的带权路径长度之和，通常记作”WPL“。例如图1中这棵树的带权路径长度为：WPL=71+52+23+34
  
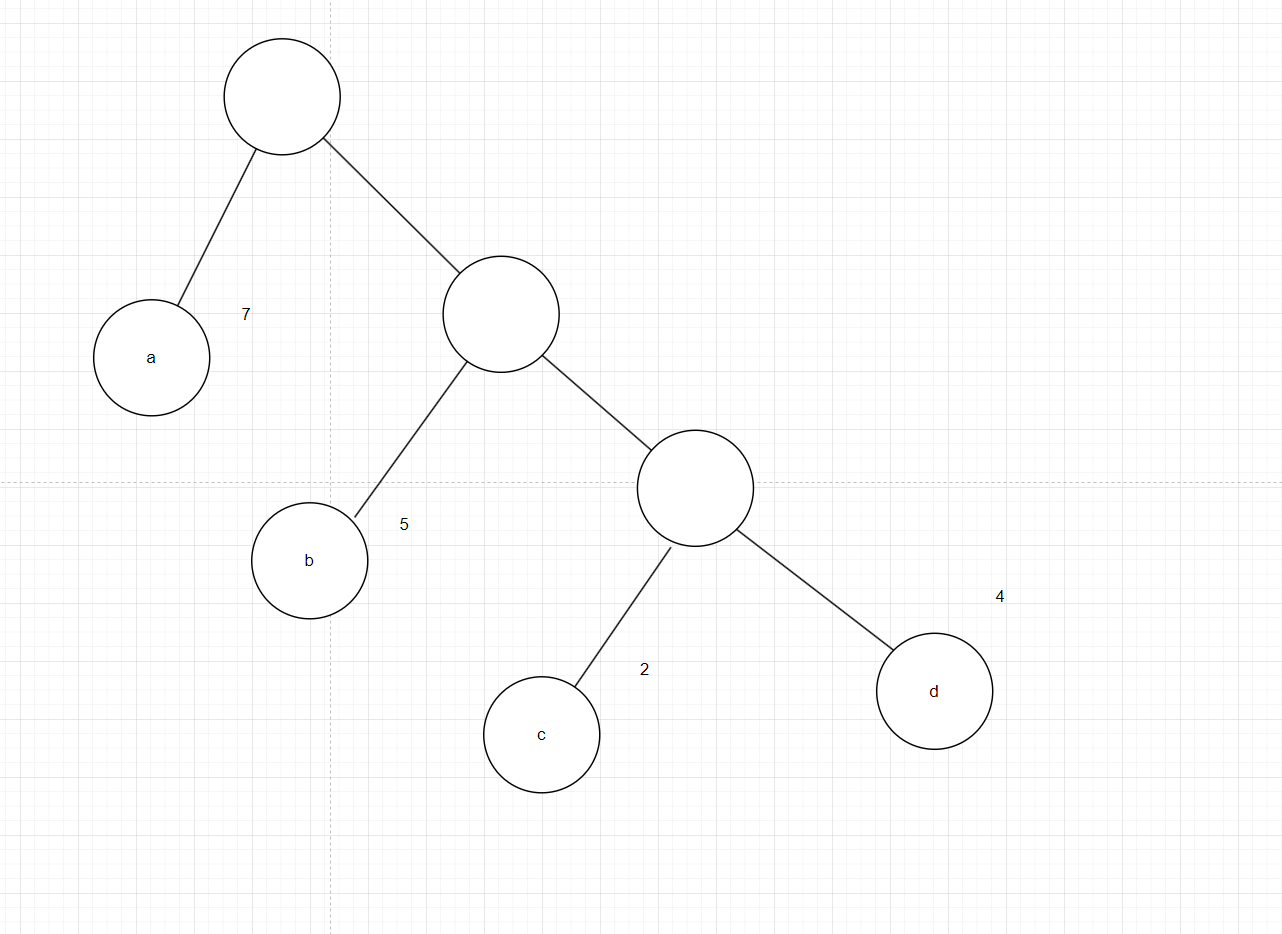
  图1

1.2哈夫曼树

当用n个节点(都做叶子节点且都有各自的权值)试图构建一颗树时，如果构建的这棵树的WPL最小，称这棵树为”最优二叉树“，有时也叫”哈夫曼树“。(使得权值越小的值放在树的最下面，因为权值越小越不可能出现，因为权值越小越不可能出现，就能用越长的编码去指定)

1.3哈夫曼树的应用

• 哈夫曼编码：哈夫曼编码（Huffman Coding）是一种由David A. Huffman于1952年提出的​可变长度无损压缩编码​，核心思想是根据字符出现频率分配不同长度的二进制编码，​高频字符用短码，低频字符用长码​，从而实现数据压缩

  • 已知要对数据：AAABBACCCDEEA，设计编码，使其传输效率较高
  • 一共有ABCDE5个状态，至少需要3个bit，000，001，010，011，100，101，110，111，从这8个状态中随机选出5个状态，来表示ABCDE，而我们在数据中一个有5个A，2个B，3个C，1个D，2个E，一共13个符号，13*3=39bit。如果这样编码，这样的编码是等长编码，我们一般是不让用的，比如如果接收端接收的是001010101，如果是等长编码，我们直接三个三个地解析：001 010 101，然后去查表即可，但是等长编码有个致命的问题，在AAABBACCCDEEA这个通信集团中我们发出D和E的概率非常小，我们就想到变长编码。发的越频繁的我们就用一个比特来表示，次频繁的我们就用2个或3个bit来表示，几乎不出现的就用5个bit来表示，这就导致虽然我们用的长编码来编的，但是由于几乎不怎么出现，我们也不会编得那么多，反倒是出现频繁的我们仅采用一个bit来编码，要编的码反而减少了。
  • 但是变长编码也有一个问题，无法解析。如果一个字符的编码是其他字符的前缀，例如A:00,B:001,C:010,在解析B的时候前面出现了00，那么我怎么知道这是A的00还是B的001的前面的00呢，所以我们在通信的时候编的码一定要是非前缀码。

接下来用这个例子已知要对数据：AAABBACCCDEEA，设计编码，使其传输效率较高。来感受一下哈夫曼树和哈夫曼编码

先统计数据中ABCDE的出现次数，将出现的最少的D和次最少的B放在树的最下面，最少的D放左边，次最少的B放右边，然后把这两个的父节点都指向同一个父节点我们可以给这个父节点里面的值设为两者出现频率次数之和，然后消除数据中的B和D，再次从消除后的数据中找出现次数最少的元素，再把它的父节点和第一次生成的父节点指向同一个父节点，这个父节点的中的数据可以设为DBE的出现次数之和，再消除E，以此重复这个过程。最终如图2所示生成了一棵哈夫曼树。

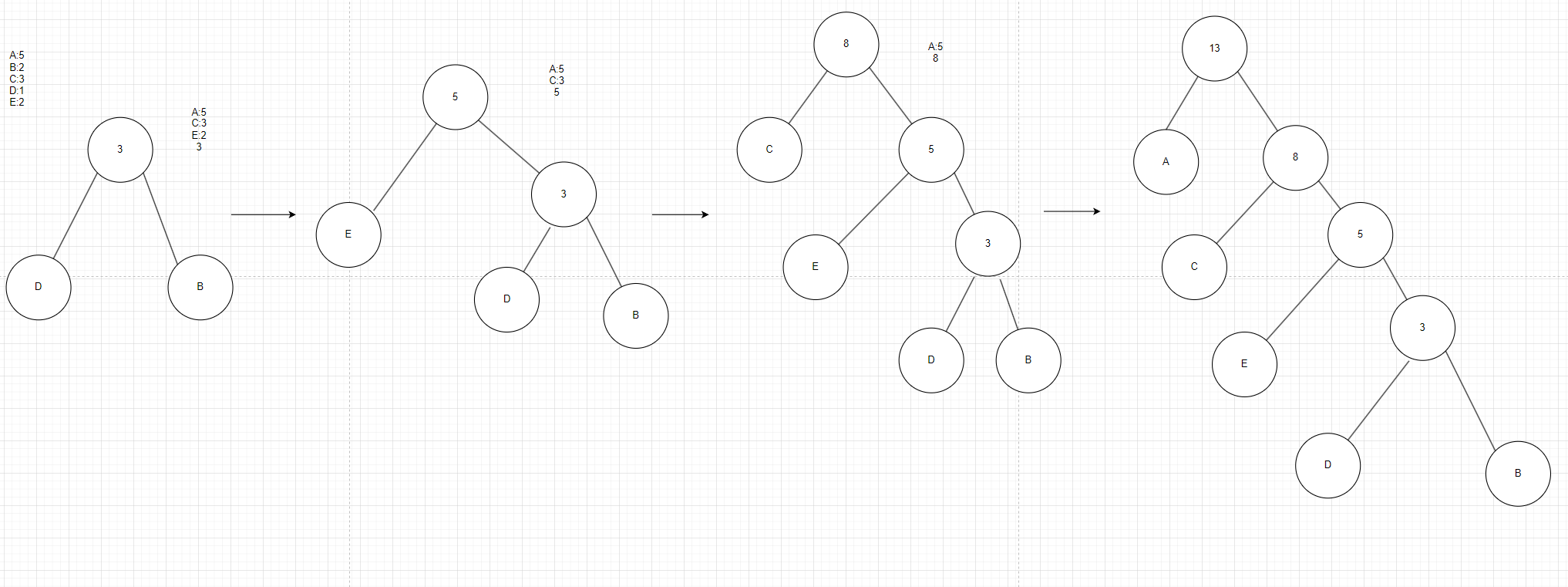
图2

构建了这棵哈夫曼树后，我们对其进行编码，可以发现，这棵树中的所有叶子节点都是我们要编的码，一般的习惯我们用左0右1的规则
例如：A：0，C:10，E：110，D：1110，E：1111可以发现任何一个编码都不是其他码的前缀码。这棵树的WPL=51+24+32+14+2*3=29个码，我们只需要构建29个bit就可以发送完所有的数据，但是等长编码需要39个，并且还不是前缀码，所以解析端也很方便。

哈夫曼树特性：n个叶子节点，哈夫曼树的总节点个数：2n-1。因为节点总数为度为0，1，2的节点数和，在哈夫曼树中没有度为1的节点所以n0+n1+n2=n0+n2,而在之前二叉树中有一个结论n0 = n2 + 1，所以所有节点之和等于2n0-1。

1.4创建哈夫曼树代码逻辑

我们来思考一下用线性存储来存哈夫曼树还是用链式存储来存，之前我们学的树都是已知根节点生成子节点，并且我们不知道一共要插入多少个元素，现在我们是已知叶子节点要生成父节点，并且由于n个叶子节点，哈夫曼树的总节点个数：2n-1。我们知道总的节点数，节点数量是固定的，那顺序存储应该比链式存储会好一点，之前链式存储知道根，根的左右指针直接指向就可以，而现在没有根，所以我们可以用顺序存储只存下标这中方法来做

如图我们要将这些数据构建成一棵哈夫曼树，注意这些数据出现的频率次数和应该为100或10，因为这些出现的概率和应该为1，，这样主要是计算方便一些。如图有8个叶子节点，根据哈夫曼的特点，我们总节点的个数应是15个节点，由上面我们的存储逻辑分析，我们可以用线性存储来存，之前在《01数据结构-树及树的存储》中讲树的存储的时候，树的表示实际上就是把树的节点之间的关系表示清楚，我们完全可以用索引号来表示节点，然后把节点与节点之间的关系维护清楚即可。我们维护右边的这个表的时候，需要写每个节点的左右孩子和父节点，我们用索引号来表示第几个数据，我们一般建议大家从一号节点开始，我们申请16个空间，用1到15号节点，把0号当作根节点下标，当我们的父节点是0的时候就说明到根节点了

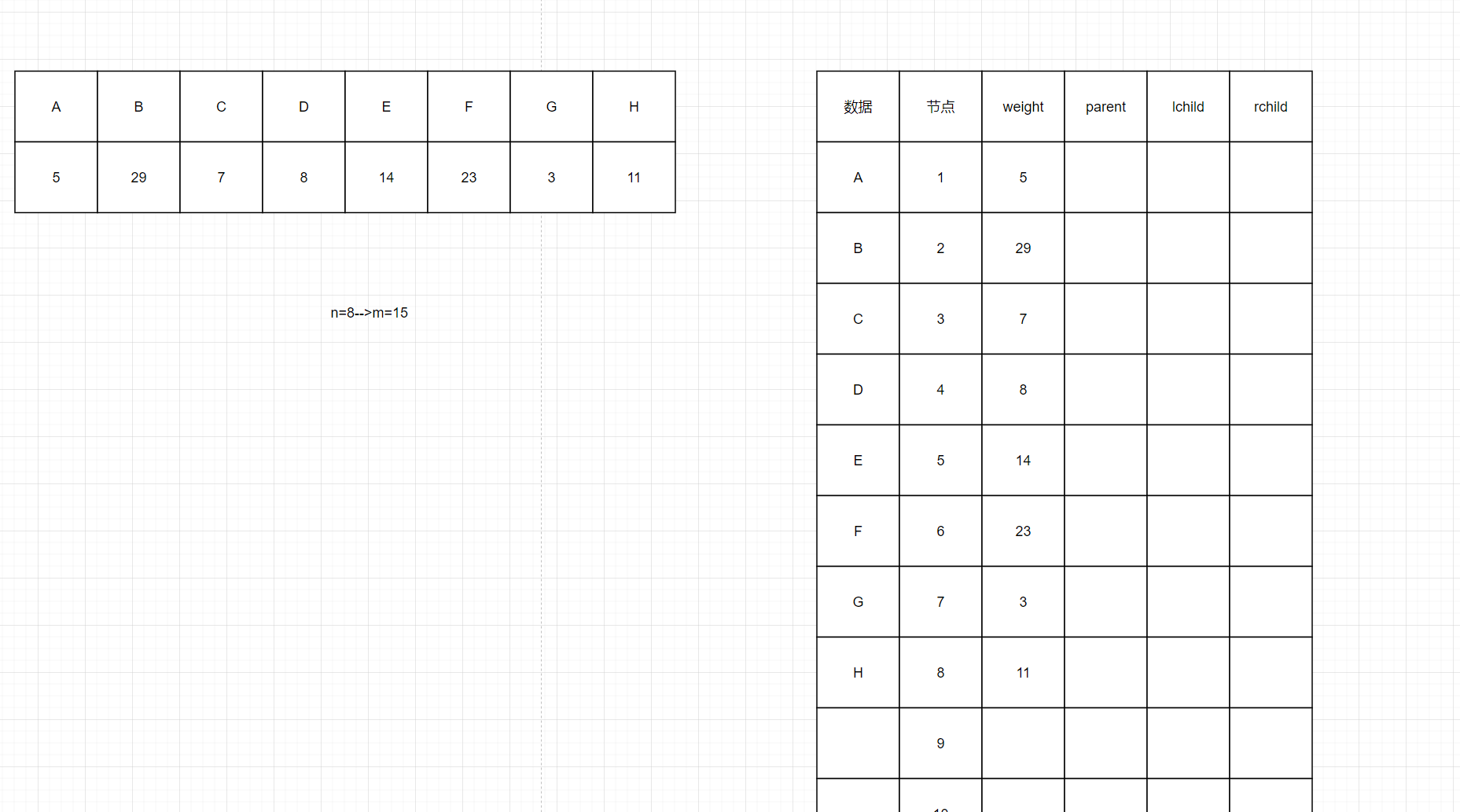
图3

如图4我们先从第9号元素开始填充表，先遍历前8个节点的weight找到数据中weight最小的两个元素A，G，让他们构建一个父节点，这个父节点的权值为两个数据的出现次数之和，再感觉构建出来的填写对应的parent,lchild,rchild，在构建9这个父节点的时候我们再遍历前八个元素，填写节点信息，此处应该把A和G的parent改为9，9的权值改为8，lchild改为7，rchild改为1（我们通常把出现次数少的放左边），parent我们暂定为0，，9后构建完成后，我们继续构建10号节点。同9节点构建的过程一样，遍历前9个节点的weight找除去AG后weight最小和次最小的两个点，需要遍历前9个元素，更新对应的节点信息。

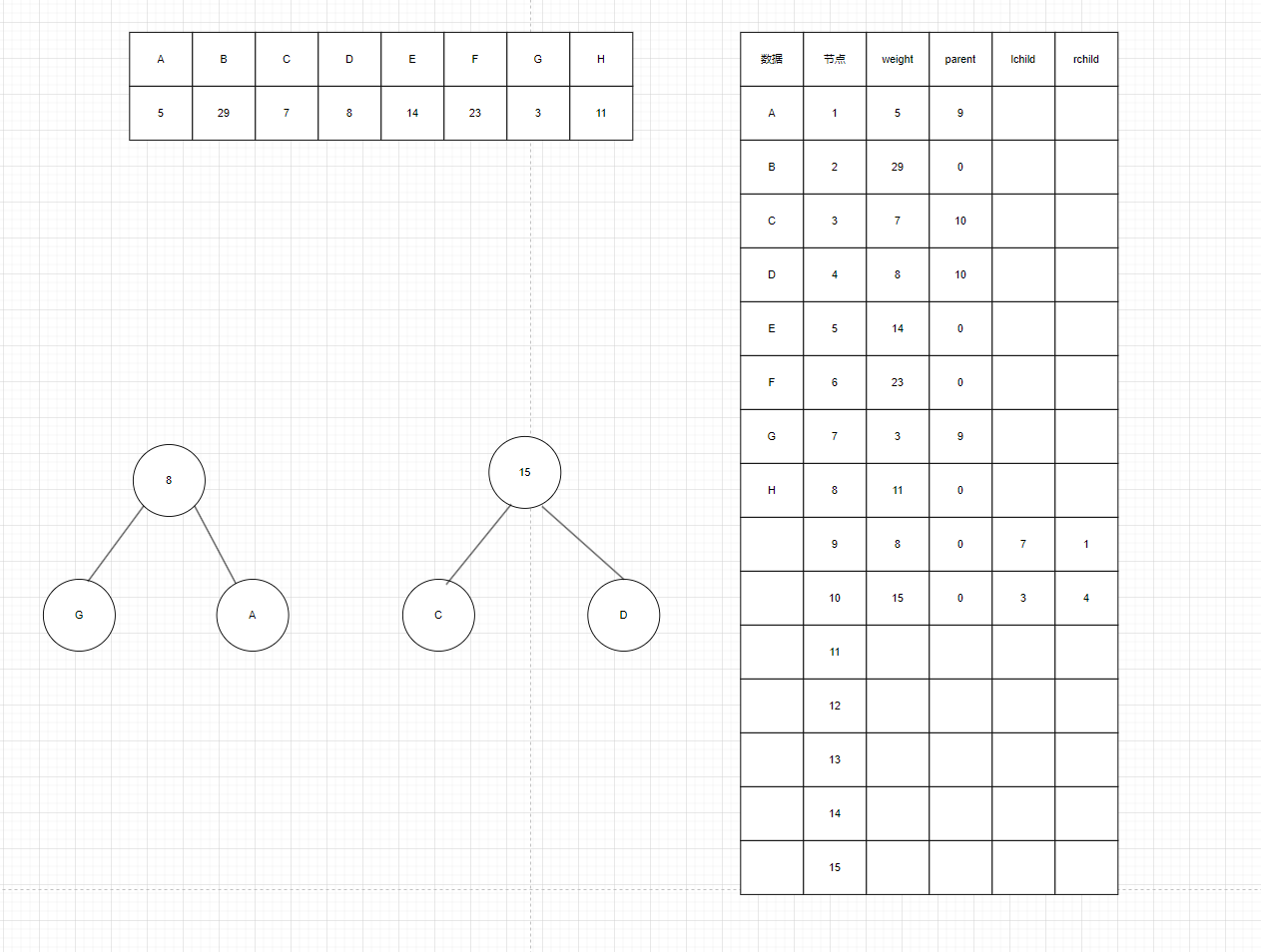
图4

如图5构建第11号节点，遍历前10个节点的weight，找出除去AGDC后weight最小的两个点，发现是第8号节点和第9号节点，依旧把weight小的放左边，更新对应节点的parent，lchild，rchild。然后构建第12号节点，构建思路是一样的，我就不赘述了。

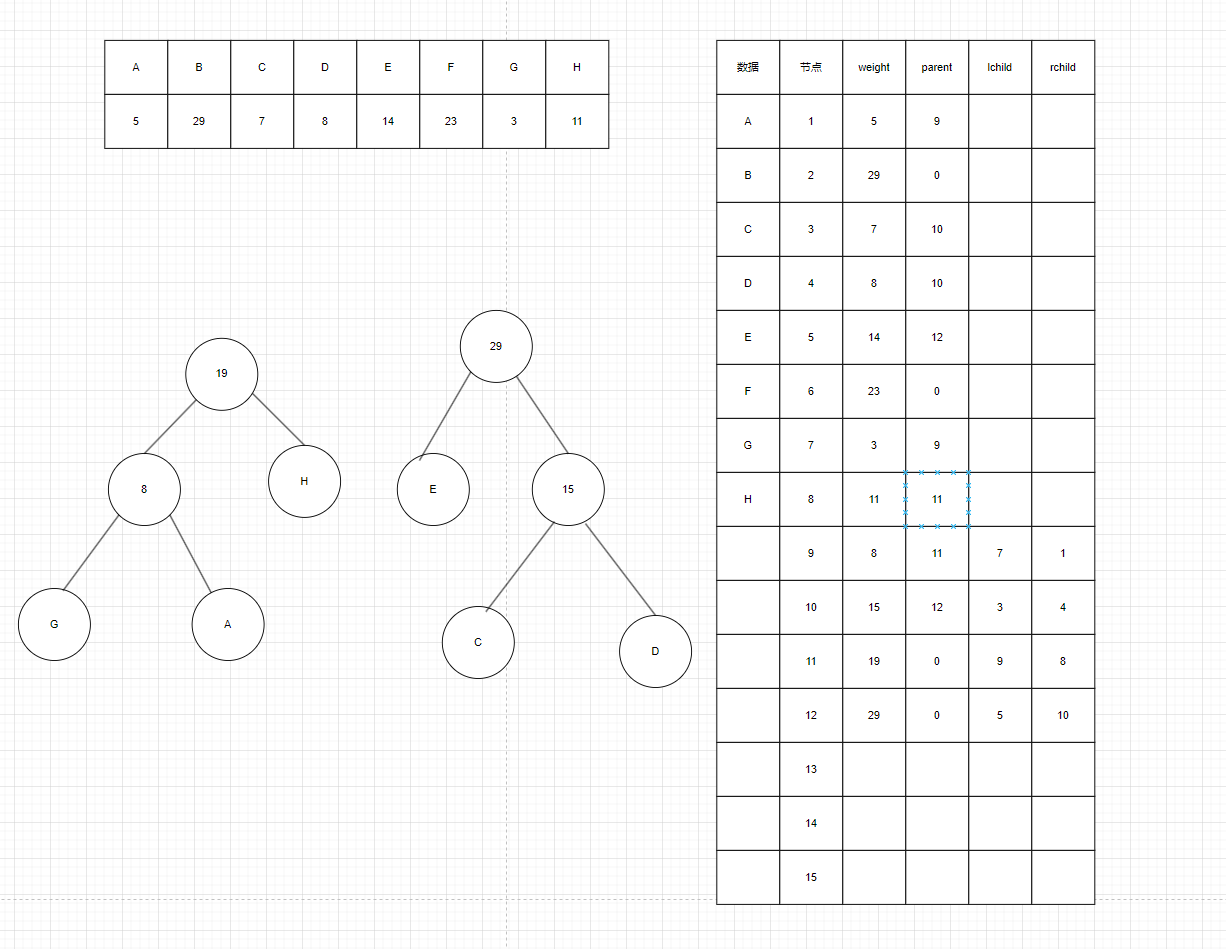
图5

如图6为最终构建出的哈夫曼树，每创建一个节点都会更新两个节点的之前有的节点parent，并更新创建节点weight,parent(0),lchild,rchild，构建好树后我们开始为每个叶子节点进行左0右1的编码。

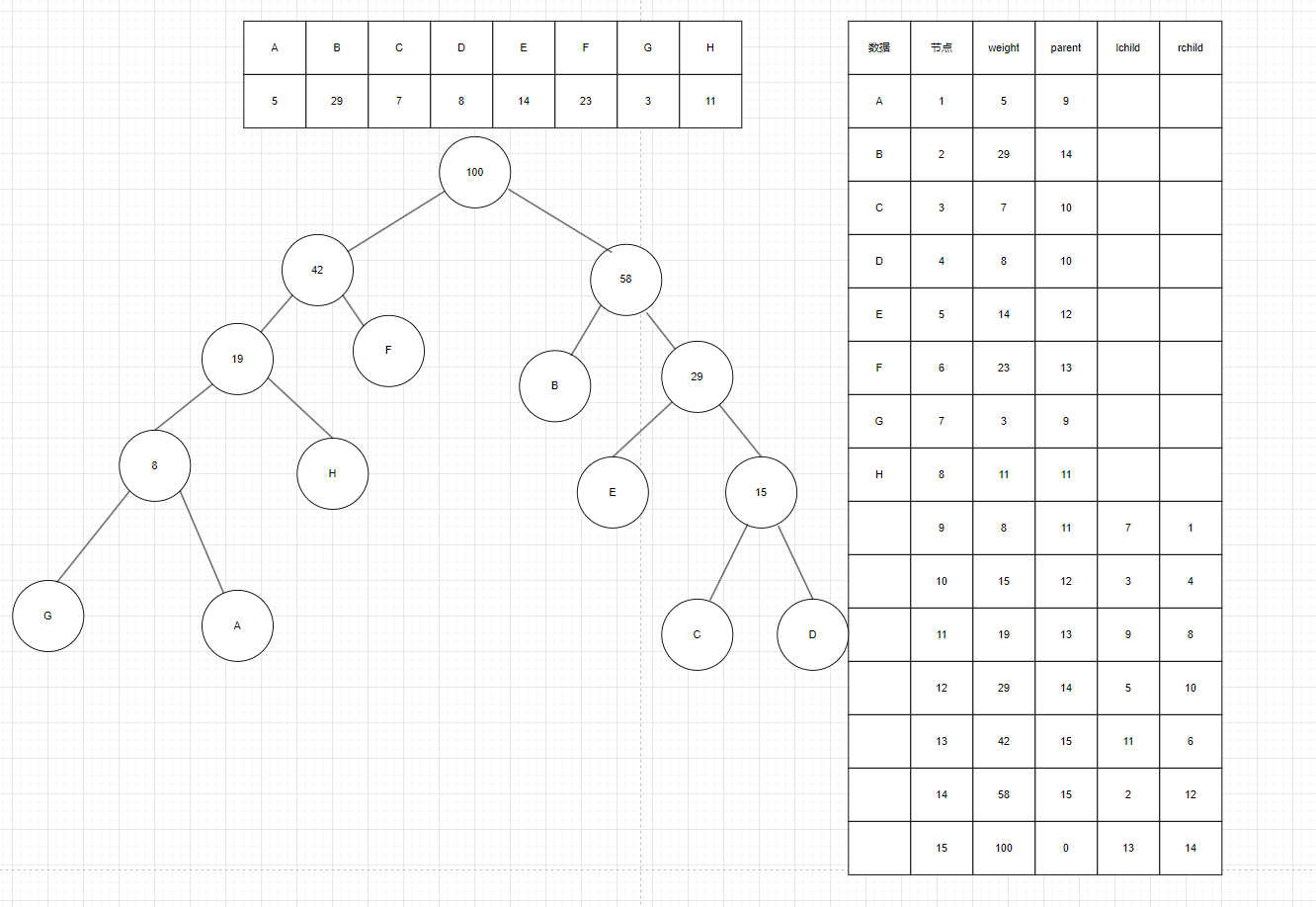
图6

1.5哈夫曼编码实现

如图7我们要实现A的编码，应该定义一个pos=A的索引值用pos去找A开始往上找父节点，，看pos是父节点的左边还是右边，确定第一个编码是0还是1，把A的父节点交给pos，看再用pos找到pos的父节点，看pos是父节点的左边还是右边确定第二个编码，以此重复直到找到对应pos节点的parent为0时编完码退出循环。这个方法每求一个字符时，由于是倒序构建，我们可以定义一个start，把它设置为ACode数组里面的最后一个元素，设标识符’\0’，从后往前填编码，这样就实现了顺序。

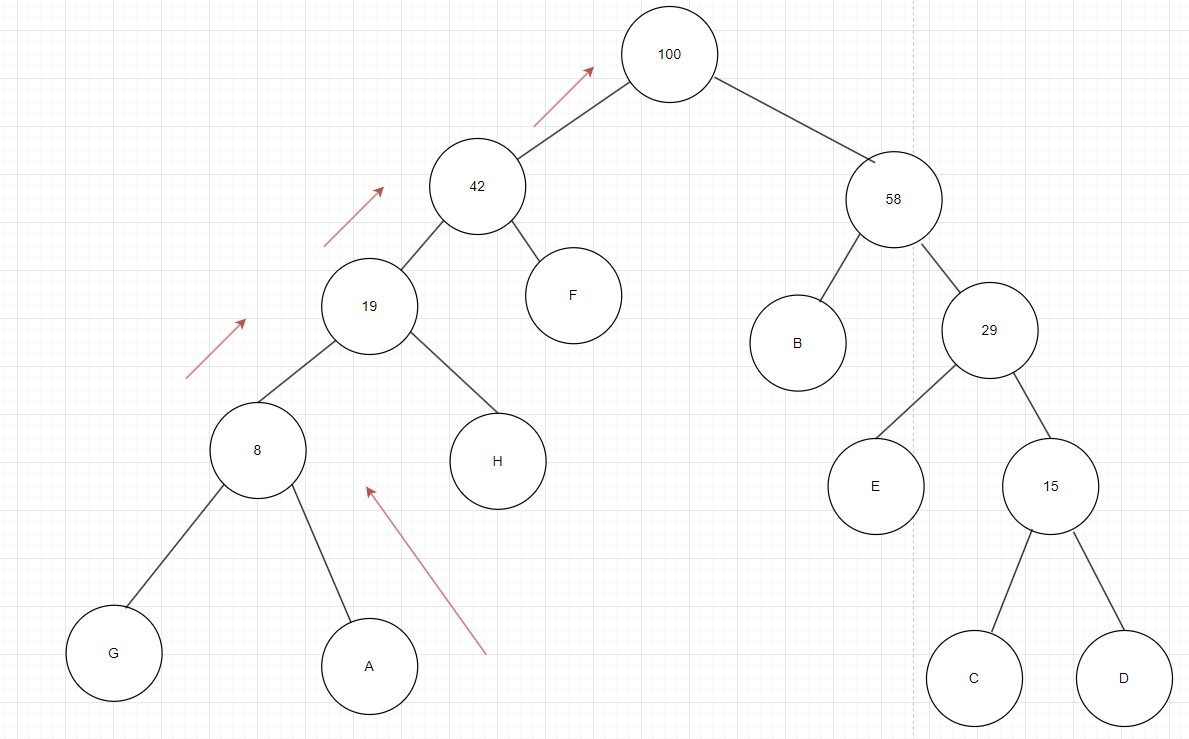
图7

接下里来看一段伪代码，我们用ACode来存A的编码，由于n个节点，树的高度最高是n，编码个数最多为n，我们定义一个start=n-1把ACode数组的最后一个元素设为’\0’，定义一个pos表示当前编码的位置（第一次是叶子节点），定义一个p拿到pos的的parent(第一次是叶子节点的parent),在while循环里当pos的parent不等于0时，start–，从后开始往前编码，如果tree[p].lchild==pos，就设为1，否则设为2，然后把pos赋值给p,p更新为新的parent。

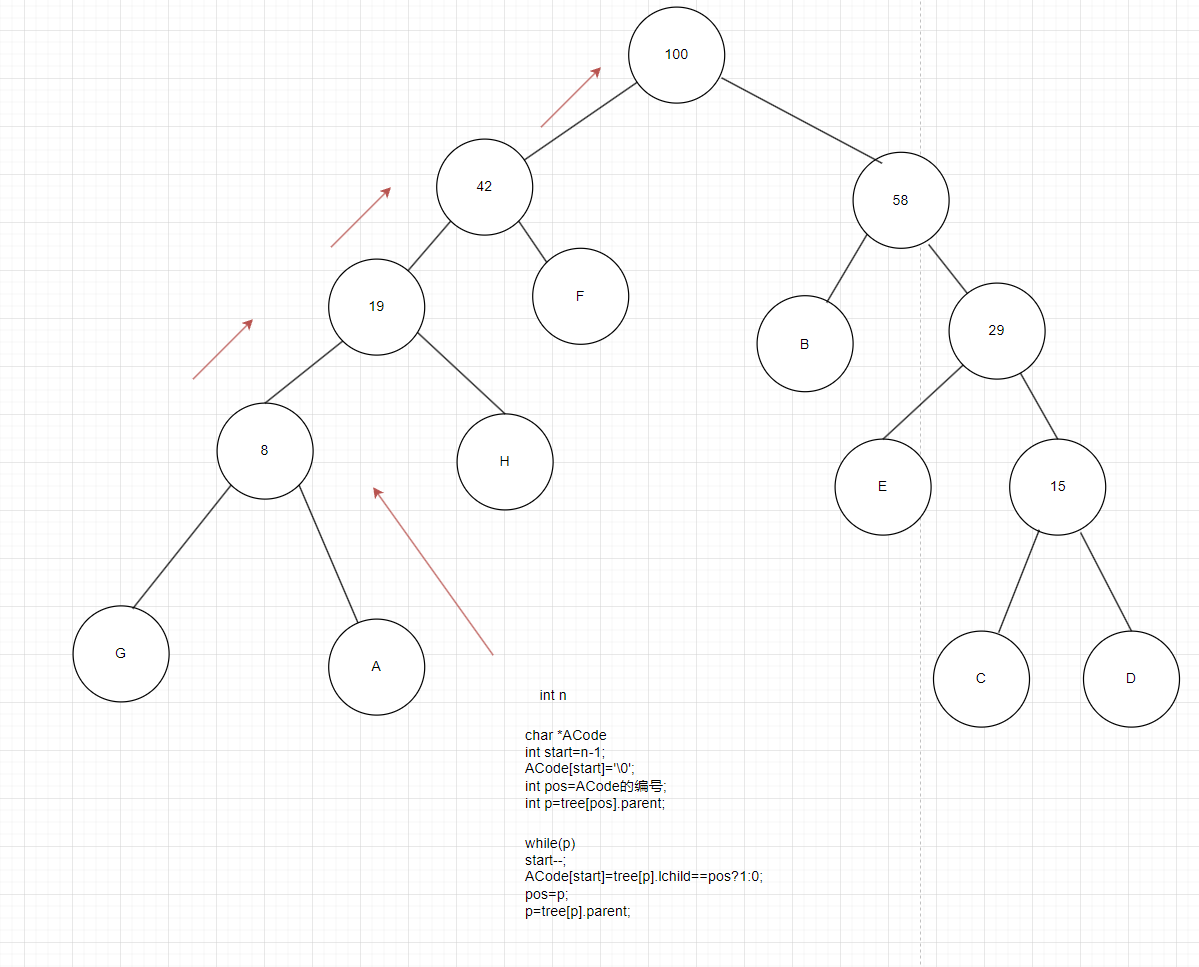
图9

由于要给每一个叶子节点都编码，我们用二维数组来存储每个叶子节点的编码的首地址，每个首地址存每个叶子节点的编码如图10所示

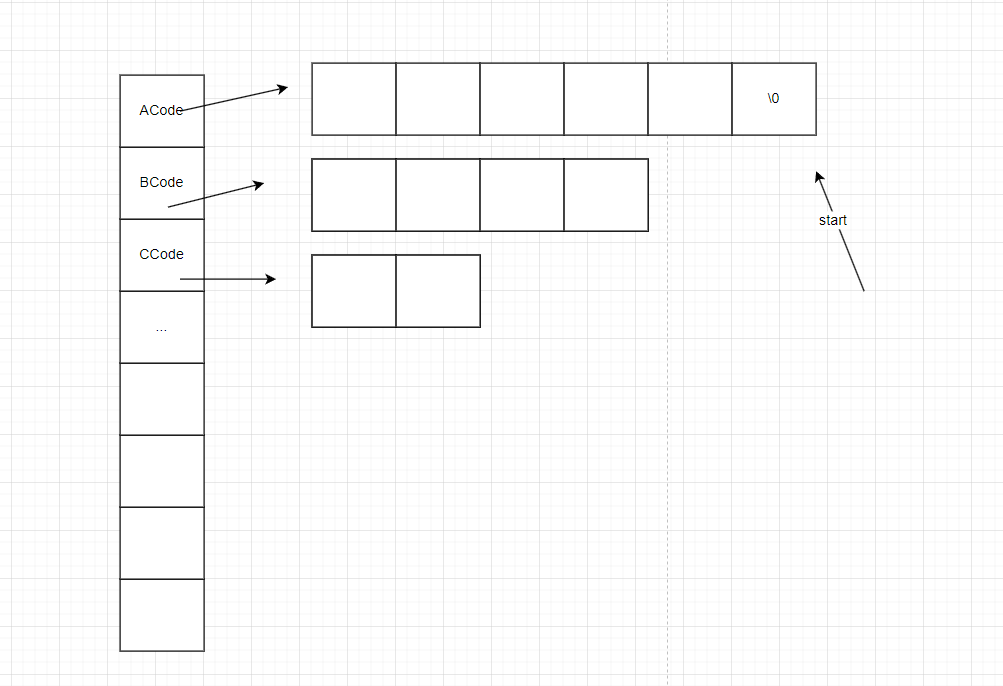
图10

1.6哈夫曼树代码实现

定义哈夫曼树结构，用顺序存储存储

// 定义Huffman树的节点结构，采用顺序存储方式，下标索引来标识不同的节点
typedef struct {int weight;int parent;int lChild;int rChild;
} HuffmanNode, *HuffmanTree;

为这个结构体写了两个名字，一个是Huffman树的节点结构，一个是结构体指针用来指向哈夫曼树。

创建哈夫曼树：HuffmanTree createHuffmanTree(const int *w, int n);

static void selectNode(HuffmanTree tree, int n, int *s1, int *s2) {int mini = 0;// 找到第一个父节点为0的编号当成最小值用于比较for (int i = 1; i <= n; ++i) {if (tree[i].parent == 0) {mini = i;break;}}for (int i = 1; i <= n; ++i) {if (tree[i].parent == 0) {if (tree[i].weight < tree[mini].weight) {mini = i;}}}*s1 = mini;// 开始找第二个最小权值的点for (int i = 1; i <= n; ++i) {if (tree[i].parent == 0 && i != *s1) {mini = i;break;}}for (int i = 1; i <= n; ++i) {if (tree[i].parent == 0 && i != *s1) {if (tree[i].weight < tree[mini].weight) {mini = i;}}}*s2 = mini;
}HuffmanTree createHuffmanTree(const int* w, int n) {HuffmanTree tree;int m = 2*n - 1;// 1.1 申请2n个单元，从1号索引开始存储数据tree = malloc(sizeof(HuffmanNode) * (m + 1));if (tree == NULL) {return NULL;}// 初始化1 ~ 2n-1个节点for (int i = 1; i <= m; ++i) {tree[i].parent = tree[i].lChild = tree[i].rChild = 0;tree[i].weight = 0;}// 1.2 设置初始化权值for (int i = 1; i <= n; ++i) {tree[i].weight = w[i - 1];}// 填充n+1下标到m下标的空间int s1, s2;for (int i = n + 1; i <= m; ++i) {// 在[1 ... i-1]范围内，父节点为0，权值最小的两个点selectNode(tree, i - 1, &s1, &s2);// 将这2个权值最小的节点，组合到第i个位置上（父节点）tree[s1].parent = tree[s2].parent = i;tree[i].lChild = s1;tree[i].rChild = s2;tree[i].weight = tree[s1].weight + tree[s2].weight;}return tree;
}

先来看HuffmanTree createHuffmanTree(const int* w, int n),我们已知要传输的数据是n个，由哈夫曼树的性质得，哈夫曼树中一共有2n-1个节点，我们申请2n个节点结构，用第一个到第2n-1个数据来存，先初始化第1到2n-1个节点中的数据元素，把他们的parent，lChild，rChild，weight都设为0，再次初始化第1到第n个节点的权值，接下来根据1.4创建哈夫曼树代码逻辑，我们需要遍历新节点之前的所有节点，找到最小的两个值，更新对应节点中的parent，lChild，rChild，weight，并重复这个过程，所以我们写了个static void selectNode(HuffmanTree tree, int n, int *s1, int *s2)；内在接口用来得到最小的两个值。知道for循环退出得到哈夫曼树。

先来小测一下：

#include <stdio.h>
#include "huffmanTree.h"int main() {int w[] = {5, 29, 7, 8, 14, 23, 3, 11};char show[] = {'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H'};int n = sizeof(w)/sizeof(w[0]);HuffmanTree tree = createHuffmanTree(w, sizeof(w)/sizeof(w[0]));for (int i = 1; i <= 2*n - 1; i++) {printf("%d -- %d -- %d -- %d\n", tree[i].weight, tree[i].parent, tree[i].lChild, tree[i].rChild);}
}

结果：

D:\work\DataStruct\cmake-build-debug\02_TreeStruct\HuffmanTree.exe
5 -- 9 -- 0 -- 0
29 -- 14 -- 0 -- 0
7 -- 10 -- 0 -- 0
8 -- 10 -- 0 -- 0
14 -- 12 -- 0 -- 0
23 -- 13 -- 0 -- 0
3 -- 9 -- 0 -- 0
11 -- 11 -- 0 -- 0
8 -- 11 -- 7 -- 1
15 -- 12 -- 3 -- 4
19 -- 13 -- 9 -- 8
29 -- 14 -- 5 -- 10
42 -- 15 -- 11 -- 6
58 -- 15 -- 2 -- 12
100 -- 0 -- 13 -- 14进程已结束，退出代码为 0

和我们在1.4创建哈夫曼树代码逻辑分析出来的哈夫曼树一样。

1.7哈夫曼编码实现

哈夫曼编码实现：HuffmanCode* createHuffmanCode(HuffmanTree tree, int n)

typedef char *HuffmanCode;HuffmanCode* createHuffmanCode(HuffmanTree tree, int n) {// 生成n个字符的编码表，每个表项里保存编码的空间首地址HuffmanCode *codes = malloc(sizeof(HuffmanCode) * n);if (codes == NULL) {return NULL;}memset(codes, 0, sizeof(HuffmanCode) * n);// 每求一个字符时，倒序构建，n个节点，树的高度最高是n，编码个数最多为nchar *temp = malloc(sizeof(char) * n);int start;				// temp空间的起始位置int p;					// 存放当前节点的父节点信息int pos;				// 当前编码的位置//为每一个叶子节点编码for (int i = 1; i <= n; ++i) {start = n - 1;temp[start] = '\0';pos = i;p = tree[i].parent;// 逐个字符求Huffman编码while (p) {--start;temp[start] = (tree[p].lChild == pos) ? '0' : '1';pos = p;p = tree[p].parent;}// 第i个字符编码分配的空间codes[i - 1] = malloc(sizeof(HuffmanCode) * (n - start));strcpy(codes[i - 1], &temp[start]);}free(temp);return codes;
}

• 我们先创建一个二维指针生成n个字符的编码表，每个表项里保存编码的空间首地址，把这里面的值全都清0，由于一开始不知道每个叶子结点的编码长度，索性直接创建一个char *temp,这个temp暂存每个叶子结点的编码，start的作用是用来给temp里面的空间从后往前赋值，p存放当前节点的父节点信息,pos表示当前编码的位置。
• 先写大逻辑，for循环从1到n为每一个叶子节点编码，在while循环里面为每一个节点逐个字符求Huffman编码
• 来看for循环里具体实现：其实就是1.5哈夫曼编码实现里面写的逻辑，那里可能写的不是很好，结合这里再看一看，先把start设置为temp数组中最后一个字符，把它设为终止符temp[start] = ‘\0’;pos初始存放叶子节点，p初始存放叶子节点的父节点，进入while循环，在temp里面从后往前逐个字符编码：看tree[p].lChild是否等于pos，如果相等，则把 temp[start]编为1否则编为0，然后更新pos,pos先前指向的是叶子节点，更新后应该存pos的父节点p，更新p，p先前指向的是叶子节点父节点，更新后应存叶子节点的父节点的父节点即tree[p].parent。while循环结束以后为第i个字符编码分配空间，注意我们for循环是从1开始，codes里面的索引是i-1,由于是变长，分配的空间为n-start。然后逐个字符copy进去最后把临时空间free掉即可。

最后再来写一个释放接口：

void releaseHuffmanCode(HuffmanCode *codes, int n) {if (codes) {for (int i = 0; i < n; ++i) {if (codes[i]) {free(codes[i]);}}}
}

最后来测试一下：

#include <stdio.h>
#include "huffmanTree.h"int main() {int w[] = {5, 29, 7, 8, 14, 23, 3, 11};char show[] = {'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H'};int n = sizeof(w)/sizeof(w[0]);HuffmanTree tree = createHuffmanTree(w, sizeof(w)/sizeof(w[0]));// for (int i = 1; i <= 2*n - 1; i++) {// 	printf("%d -- %d -- %d -- %d\n", tree[i].weight, tree[i].parent, tree[i].lChild, tree[i].rChild);// }HuffmanCode *codes = createHuffmanCode(tree, n);for (int i = 0; i < n; i++) {printf("%c: %s\n", show[i], codes[i]);}releaseHuffmanCode(codes, n);
}

结果：

D:\work\DataStruct\cmake-build-debug\02_TreeStruct\HuffmanTree.exe
A: 0001
B: 10
C: 1110
D: 1111
E: 110
F: 01
G: 0000
H: 001进程已结束，退出代码为 0

大概先写这些吧，今天的博客就先写到这，谢谢您的观看。