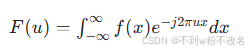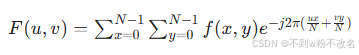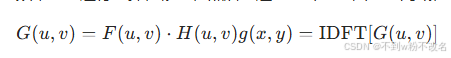【数字图像处理系列笔记】Ch05:傅里叶变换与频率域滤波
目录
1. 背景
2. 基本概念
（一）空间域与频率域
（二）频率成分相关概念
3.傅里叶变换
（一）连续傅里叶变换（CFT）
（二）离散傅里叶变换（DFT）
（三）快速傅里叶变换（FFT）
4.频率域滤波
（一）基本原理
（二）滤波器分类及作用
1. 低通滤波器（LPF）
作用
2. 高通滤波器（HPF）
作用
3. 带通 / 带阻滤波器
（三）滤波流程步骤
（四）应用场景与优缺点
1. 应用场景
2. 优点
3. 缺点
1. 背景
在图像处理领域，空域（空间域）处理直接操作图像像素，像平滑、锐化等，但面对复杂噪声、周期性干扰等问题时，有一定局限性。而傅里叶变换为我们打开了频率域处理的新视角。从物理信号角度看，任何复杂信号都可拆解为不同频率正弦、余弦信号的叠加，图像也不例外，其亮度变化可看作空间频率的组合，低频对应缓慢变化的大区域背景，高频对应边缘、噪声等快速变化部分。
借助傅里叶变换，将图像从空域转换到频率域，能更直观分析和处理这些频率成分，实现去噪、增强等高级操作，在医学影像去噪、遥感图像分析、数字艺术创作等场景广泛应用。
2. 基本概念
（一）空间域与频率域
- 空间域：以图像像素的空间坐标（x，y）为变量，描述图像像素的灰度分布，是我们直观看到的图像呈现形式，操作直接针对像素点，如改变像素灰度值。
- 频率域：以频率为变量，将图像表示为不同频率成分的组合，用傅里叶变换实现空域到频率域的转换，频率描述了灰度变化的快慢，低频成分对应图像中缓慢变化的区域（如大片均匀背景），高频成分对应快速变化的部分（如边缘、噪声 ）。
（二）频率成分相关概念
- 低频：图像中灰度变化缓慢的区域，对应图像的大致轮廓、整体背景，是图像的基础结构信息，若过度抑制，图像会失去整体形态。
- 高频：图像中灰度变化剧烈的区域，像物体边缘、纹理细节、噪声等，对图像的细节和锐利度起关键作用，过度增强可能放大噪声，过度抑制会让图像模糊。
3.傅里叶变换
（一）连续傅里叶变换（CFT）
对于连续函数 f(x)（一维情况，推广到二维是 f(x,y) ），其傅里叶变换 F(u) 定义为：
逆变换（从频率域回到空间域）为：
其中 j 是虚数单位，u 是频率变量，是复指数函数，可理解为不同频率的正弦、余弦信号（欧拉公式
），通过积分运算，把空间域函数分解成不同频率的成分组合。
（二）离散傅里叶变换（DFT）
图像处理中图像是离散的像素矩阵，所以用离散傅里叶变换。对于 N×N 的离散图像 f(x,y)（x,y=0,1,…,N−1 ），二维离散傅里叶变换（2D DFT）为：
逆离散傅里叶变换（2D IDFT）为：
这里 u,v 是频率域的变量，范围同样是 0 到 N−1 ，计算得到的 F(u,v) 是复数，可表示为幅度和相位，幅度反映对应频率成分的强度，相位反映成分的位置信息，通常幅度谱（|F (u,v)|）用于分析频率分布。
（三）快速傅里叶变换（FFT）
是离散傅里叶变换的高效算法实现，通过巧妙分治策略，将 DFT 的时间复杂度从
降低到
，让大规模图像的傅里叶变换计算可行，成为数字图像处理中频率域操作的关键支撑，实际软件（如 Matlab、Python 的 OpenCV 库 ）里的傅里叶变换功能，基本基于 FFT 实现。
4.频率域滤波
（一）基本原理
频率域滤波是在图像的傅里叶变换结果（频率域表示 F(u,v) ）上，通过设计合适的滤波器 H(u,v) ，对不同频率成分进行选择性修改，然后经逆傅里叶变换回到空间域，得到处理后的图像 g(x,y) 。
数学表达式为：
即先在频率域用滤波器和原图像频谱相乘，再逆变换回空域，实现对图像的滤波处理。
（二）滤波器分类及作用
1. 低通滤波器（LPF）
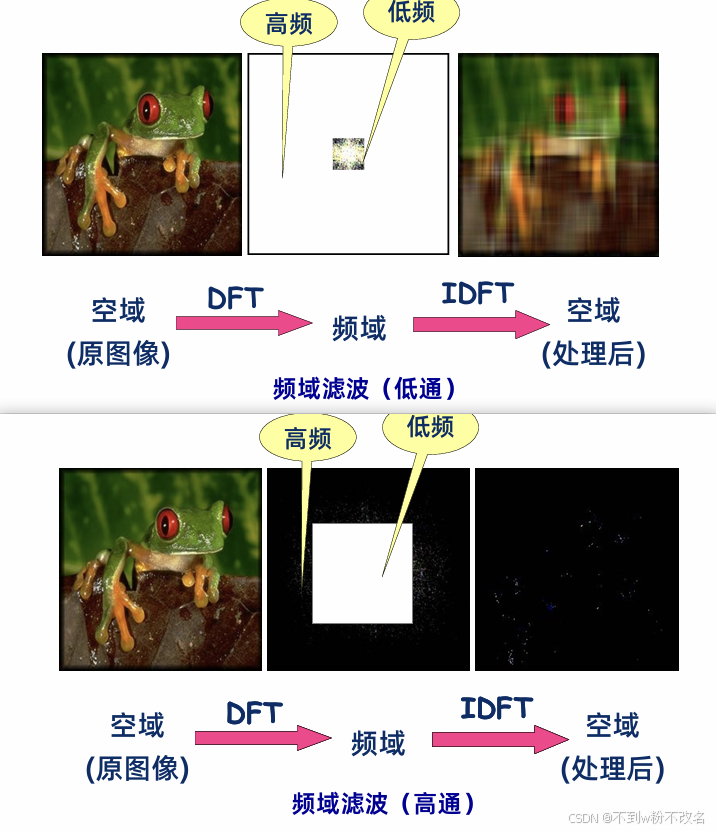
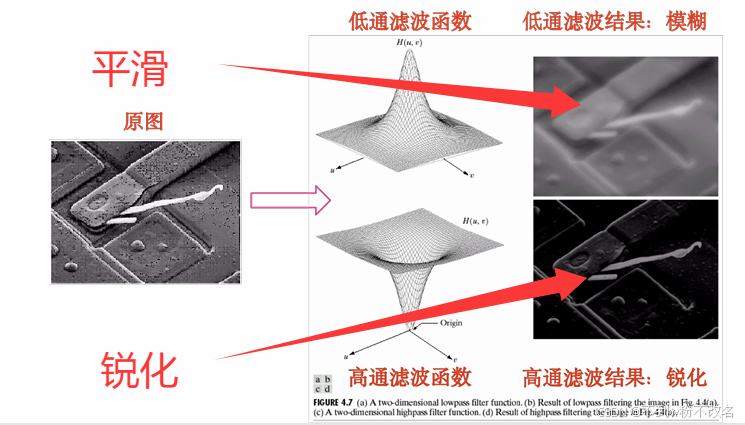
- 原理：让低频成分通过，抑制高频成分。
- 常见类型：
- 理想低通滤波器（ILPF）：频率域中，以截止频率 D0 为半径的圆内，滤波器值为 1，圆外为 0，公式
但逆变换会产生振铃效应（图像边缘出现震荡波纹 ），实际少用。 - 巴特沃斯低通滤波器（BLPF）：公式
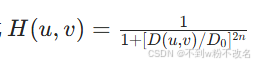，n 是阶数，控制过渡带陡峭程度，n 越大过渡带越窄，接近理想低通，振铃效应比理想低通弱，能平滑图像、去除高频噪声（如椒盐噪声中的高频部分 ），让图像模糊化。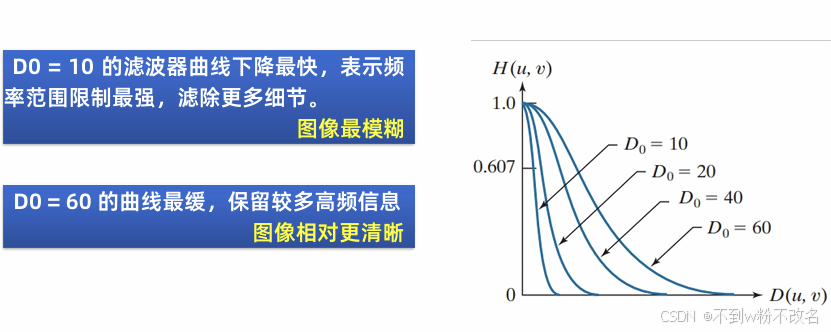
- 高斯低通滤波器（GLPF）：公式
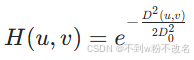，高斯分布特性使过渡带平滑，无振铃效应，广泛用于图像去噪、预处理模糊，抑制噪声同时相对柔和保留部分细节。
- 理想低通滤波器（ILPF）：频率域中，以截止频率 D0 为半径的圆内，滤波器值为 1，圆外为 0，公式
作用
- 信号增强：突出信号里的快速变化部分（如边缘、突变）。图像处理中，用于边缘检测（像 Sobel、Laplace 算子原理涉及高通滤波特性 ），让图像边缘更清晰，便于目标识别；音频处理里，增强高音部分，让声音更明亮，比如提升演讲录音里的高频细节，使语音更清晰。
- 噪声消除：去除低频干扰。如生物医学信号（心电图）里的基线漂移，让信号更纯净；传感器信号中，过滤缓慢变化的漂移，保证测量精准。比如工业传感器采集振动信号时，消除设备缓慢晃动带来的低频干扰，准确捕捉振动高频特征。
- 频率分离与特征提取：通信系统里分离高频载波信号，让特定高频段信号传输更顺畅；数据分析中，检测信号的高频瞬态变化（如机械振动的异常高频抖动 ），用于故障诊断；音响系统里，把高频信号导向高音扬声器，实现分频播放，优化音质。
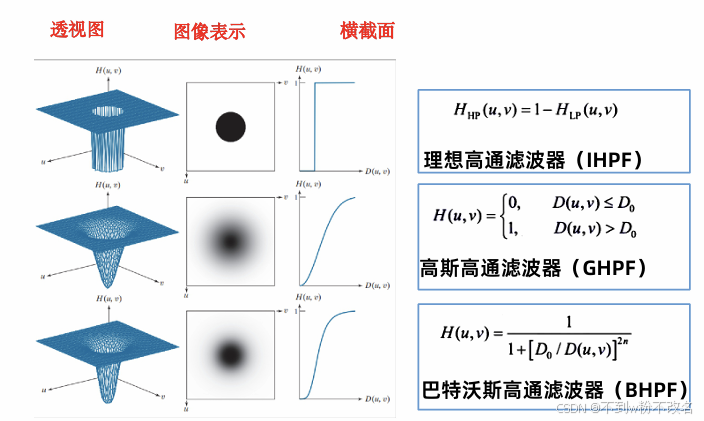
2. 高通滤波器（HPF）
- 原理：抑制低频成分，让高频成分通过，增强图像边缘、细节，突出纹理，但也会放大噪声。
- 常见构造：由低通滤波器推导，
。如理想高通滤波器（IHPF）、巴特沃斯高通滤波器（BHPF）、高斯高通滤波器（GHPF），分别对应上述低通滤波器的互补形式，用于图像锐化、边缘提取，比如突出遥感图像中地形轮廓。
作用
- 去噪：去除信号里的高频噪声。如音频处理中，消除音频的高频嘶嘶声；图像处理里，弱化图像的颗粒噪点，让画面更干净。像老照片修复时，用它过滤掉因胶片老化产生的高频杂点。
- 平滑信号：对传感器数据、数字信号等做平滑处理，消除高频波动。比如温度监测中，过滤环境突变产生的干扰，让温度曲线更稳定，便于分析趋势；在音频里，让音频信号更柔和，减少突兀的高频变化。
- 防止混叠：数字信号处理采样前，滤除高于一半采样频率的信号成分，避免高频信号被错误识别成低频信号，引发混叠失真。例如音频采集时，防止高频声音采样后出现失真，保证音质。
- 保护电路与提取主体信息：限制高频信号通过电路，保护易受高频损害的元件；提取信号核心低频特征，像语音里的主要音调、生物信号（如心电图）的关键波形，突出有用信息。比如在简单电子电路里，保护低频工作的敏感元件，免受高频信号冲击。
3. 带通 / 带阻滤波器
- 带通滤波器：允许特定频率范围（介于两个截止频率之间 ）的成分通过，可提取图像中特定频率的纹理、周期性图案，像检测织物图像的纹理频率。
- 带阻滤波器：抑制特定频率范围成分，用于去除图像中周期性噪声（如扫描图像的摩尔纹，对应特定频率干扰 ），通过设计抑制该频率区间的滤波器实现。
（三）滤波流程步骤
- 图像预处理：对原始图像（空域）进行零填充，让尺寸适合 FFT 高效计算（通常填充到 2 的幂次或其他合适尺寸 ），也有助于减少边缘效应。
- 傅里叶变换：用 FFT 将图像从空域转换到频率域，得到 F(u,v) ，并通过中心化（乘以
），使低频成分移到频率域中心，方便观察和滤波器设计。
- 滤波器设计：根据需求（去噪、增强等 ）选择滤波器类型，确定截止频率、阶数等参数，构建 H(u,v) 。
- 频率域相乘：计算
，对频率成分进行修改。
- 逆傅里叶变换：对 G(u,v) 做逆 FFT，转换回空域，得到处理后的图像 g(x,y) ，可能还需对结果做灰度调整、取实部（因计算误差可能有虚部 ）等操作。
（四）应用场景与优缺点
1. 应用场景
- 图像去噪：利用低通滤波器抑制高频噪声（如高斯噪声 ），像医学影像中去除扫描噪声，让诊断信息更清晰。
- 图像增强：用高通滤波器增强边缘、细节，使模糊图像变清晰，如老照片修复、监控图像细节强化。
- 去除周期性噪声：带阻滤波器针对性消除图像中周期性干扰（如印刷品扫描的条纹 ）。
- 图像压缩：在频率域分析能量分布，保留主要低频成分，丢弃次要高频成分，实现压缩，类似 JPEG 压缩的部分原理。
2. 优点
- 全局视角：能整体分析图像频率成分，针对性处理特定频率问题，比空域处理更具针对性，尤其对周期性噪声、全局模糊等问题。
- 数学基础扎实：基于傅里叶分析理论，滤波器设计有明确数学表达式，可精确控制频率响应。
3. 缺点
- 计算复杂度：虽有 FFT 加速，但大尺寸图像计算仍耗时，实时性要求高的场景受限。
- 边缘效应：若不做零填充等处理，变换后图像边缘易出现伪影，需额外预处理。
- 相位信息敏感：处理中若相位信息被破坏，逆变换回空域会导致图像变形，需谨慎操作滤波器对相位的影响（通常幅度谱处理为主，相位谱尽量保留 ）。