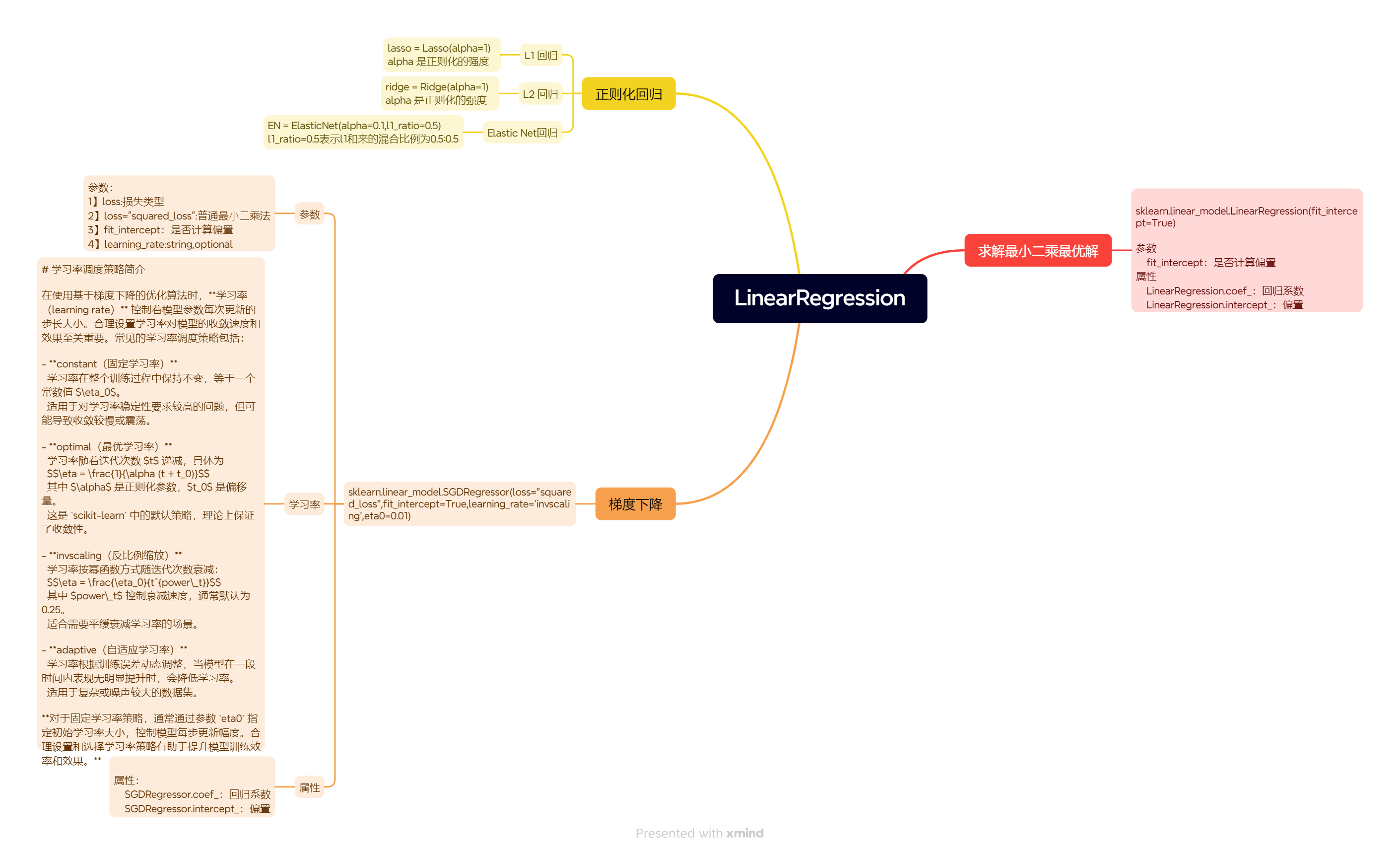
机器学习-LinearRegression

1、 关键数学知识点：

边缘概率密度 = 联合密度对非关注变量积分：$f_X(x)=\int f_{X,Y}(x,y)dy$；
条件概率密度 = 切片 $f_{X|Y}(x|y)=f_{X,Y}(x,y)/f_Y(y)$。

概率密度函数和似然函数的区别：概率密度函数回答：“给定参数，数据出现的可能性有多大？”似然函数回答：“给定观测到的数据，哪些参数值更合理？”

2、 线性回归需要满足的假设:

1 残差独立同分布：独立同分布下边缘概率密度的乘积=联合概率密度，用于模型求似然函数
2 残差正态性：模型的根本假设，模型的边缘概率密度由正态函数求得，这个正态函数来源于残差

3、 目标函数的推导过程：

1. 建模假设

$y(i)=\theta \top x(i)+\epsilon (i)$,
$\epsilon (i)\sim i.i.d.N(0,\sigma 2)$
$p(\epsilon )=\frac{1}{\sqrt{2\pi }\sigma }\exp \left(-\frac{{\epsilon }^2}{2{\sigma }^2}\right)$

2. 单个样本的概率密度(也就是边缘概率密度，借由$\epsilon$的分布计算而来):

（只需要将$\epsilon$代入, ${\epsilon }^{(i)}=y^i-{\theta }^{\top }{x}^i$ 且$\epsilon$的概率密度函数和$y^{(i)}$的概率密度函数实际上是相等的,$\epsilon$只是$y^i$平移了$y^{(i)}-{\theta }^{\top }{x}^{(i)}$,对于概率密度函数，只要形状不变，坐标轴变了也是相等的）


$p(y^{(i)}\mid x^{(i)};\theta )=\frac{1}{\sqrt{2\pi }\sigma }\exp \left(-\frac{(y^{(i)}-{\theta }^{\top }{x}^{(i)}{)}^2}{2{\sigma }^2}\right)$

$p(y^{(i)}\mid x^{(i)};\theta )$ 可理解为：在给定输入 x⁽ⁱ⁾ 并且模型参数取 θ 的条件下，观测到 y⁽ⁱ⁾ 的概率密度是多少？

3. 写出整个数据集的似然函数(即把观测值y固定、把参数θ当作变量的联合概率密度函数，称之为似然函数，由边缘概率密度的乘积计算得来)

(边缘概率密度的乘积=联合概率密度，也就是似然函数，这是独立同分布的数学定理)


$\begin{array}{rl}L(\theta )& =\prod _{i=1}^{m}p(y^{(i)}\mid x^{(i)};\theta )\\ & =\prod _{i=1}^m\frac{1}{\sqrt{2\pi }\sigma }\exp \left(-\frac{(y^{(i)}-{\theta }^{\top }{x}^{(i)}{)}^2}{2{\sigma }^2}\right)\\ & =(2\pi {\sigma }^2{)}^{-\frac{m}{2}}\exp \left(-\frac{1}{2{\sigma }^2}\sum _{i=1}^m(y^{(i)}-{\theta }^{\top }{x}^{(i)}{)}^2\right).\end{array}$

4. 取对数得到对数似然

$\ell (\theta )=\log L(\theta )=-\frac{m}{2}\log (2\pi {\sigma }^2)-\frac{1}{2{\sigma }^2}{\sum }_{i=1}^m(y^{(i)}-{\theta }^{\top }{x}^{(i)}{)}^2.$

5. 最大化对数似然 ⇔ 最小化残差平方和

( 在误差服从高斯分布的假设下，极大似然估计与最小二乘估计恰好得到同一解)
${\hat{\theta }}_{\text{MLE}}=\arg {\max }_{\theta }\ell (\theta )=\arg {\min }_{\theta }{\sum }_{i=1}^m(y^{(i)}-{\theta }^{\top }{x}^{(i)}{)}^2.$
($\arg \max$找出让某个函数达到最大值的输入值（$\theta$），而不是最大值本身)

6. 结论(对目标函数求极值)

根据最大似然估计的一阶最优条件$U(\theta )={\nabla }_{\theta }\ell (\theta )=0$对对数似然函数求导并令其为零(求极值)，可以推导出以下正规方程：
$${\hat{\theta }}_{\text{MLE}}=(X^{\top }X{)}^{-1}{X}^{\top }y,$$
其中
$$X=\left[\begin{array}{c}{x}^{(1)\top }\\ ⋮\\ x^{(m)\top }\end{array}\right]\in {\mathbb{R}}^{m\times n},y=\left[\begin{array}{c}{y}^{(1)}\\ ⋮\\ y^{(m)}\end{array}\right]\in {\mathbb{R}}^{m\times 1}.$$
求解正规方程时X要加上一列x0，x0列全为1即可
在高斯噪声假设下，线性回归的最大似然估计等价于最小二乘估计


7. 最后对$U(\theta )$再次求导可以进一步求检验统计量
#%% md

4、解释为什么有些时候为什么必须要满足线性回归假设，即使明明可以用OLS，而OLS不需要这些假设

1、为了使得OLS和MLE相同，因为MLE有无法替代的优势：
(1)一致性（样本越大，估计越接近真值）；
(2)渐近有效性（样本足够大时，它的方差是所有估计里最小的）；
(3)可推导分布（可以算出估计量的分布，从而做假设检验）。


2、 让 t/F 检验的 p 值和置信区间在小样本下完全准确


3、在满足 高斯马尔可夫定理 条件（零均值、同方差、无自相关）的线性回归模型里，OLS 是所有线性无偏估计中（在给定解释变量条件下）方差最小的那一个，即 BLUE（Best Linear Unbiased Estimator）。如果 GM 条件不满足，OLS 仍是无偏且线性的，但 不再保证方差最小；这时可能有其他线性无偏估计（例如 GLS）方差更小。




结论 :对于纯粹的预测，不一定需要满足条件，因为不需要假设检验自然也不不需要MLE的性质，只要结果好就行

5梯度下降(SGD)

数学推导过程

1. 假设模型：
   $$\hat{y}=w\cdot x+b$$

2. 定义损失函数：（这一步是和正规方程方法一样的）
   $$L=\frac{1}{2m}\sum _{i=1}^m{\left(w\cdot x_i+b-y_i\right)}^2$$

3. 对 $w$ 求偏导：
   $$\frac{\partial L}{\partial w}=\frac{1}{m}\sum _{i=1}^m\left(w\cdot x_i+b-y_i\right)\cdot x_i$$

4. 对 $b$ 求偏导：
   $$\frac{\partial L}{\partial b}=\frac{1}{m}\sum _{i=1}^m\left(w\cdot x_i+b-y_i\right)$$

梯度下降更新规则：

• $$w=w-\alpha \cdot \left(\frac{1}{m}\sum (\hat{y}-y)\cdot x\right)$$

• $$b=b-\alpha \cdot \left(\frac{1}{m}\sum (\hat{y}-y)\right)$$

其中 $\alpha$ 是学习率，$m$ 是样本数量。

梯度下降和正规方程区别：

正规方程是根据损失函数，设损失函数的所有参数的偏导(直接求导)的结果为0，通过矩阵运算一次性推出损失函数的最优参数


梯度下降是对损失函数各个参数求偏导，并不需要将偏导设为0求最优参数，而是只求偏导的结果(梯度)，然后根据学习率沿着梯度的方向走，并逐步迭代