Java 里的Tree初认识
目录
一、树的核心概念
关键术语:
二、平衡二叉树(以 AVL 树为例)
1. 左旋(Left Rotation)
2. 右旋(Right Rotation)
3. 先左旋后右旋(LR 型)
4. 先右旋后左旋(RL 型)
5、另一种技法
1、左左
2、左右
3、右右
4、右左
三、红黑树的旋转
1、概念
2、插入规则:
场景 1:
场景 2:
场景 3:
场景 4:
一、树的核心概念
树是一种层级化的非线性数据结构,由「节点」和「边」组成,核心特点是:
- 有一个唯一的「根节点」(没有父节点);
- 除根节点外,每个节点有且仅有一个「父节点」;
- 节点之间的边没有环路,形成一个「倒立的树状结构」。
关键术语:
- 节点:树的基本单元,包含数据和指向子节点的引用;
- 子节点 / 父节点:若节点 A 直接连接节点 B,A 是 B 的父节点,B 是 A 的子节点;
- 叶子节点:没有子节点的节点;
- 深度:从根节点到当前节点的边数(根节点深度为 0);
- 高度:从当前节点到最深叶子节点的边数(叶子节点高度为 0);
- 二叉树:每个节点最多有 2 个子节点(左子节点、右子节点)的树;
- 二叉查找树(BST):左子树所有节点值 <根节点值,右子树所有节点值> 根节点值(便于快速查找,时间复杂度 O (h),h 为树高)。
二、平衡二叉树(以 AVL 树为例)
平衡二叉树(如 AVL 树)是「二叉查找树的升级版」,核心目标是避免树退化为链表(此时查询效率从 O (log n) 退化到 O (n))。
它的定义是:任意节点的左右子树高度差(平衡因子)的绝对值 ≤ 1(平衡因子 = 右子树高度 - 左子树高度)。
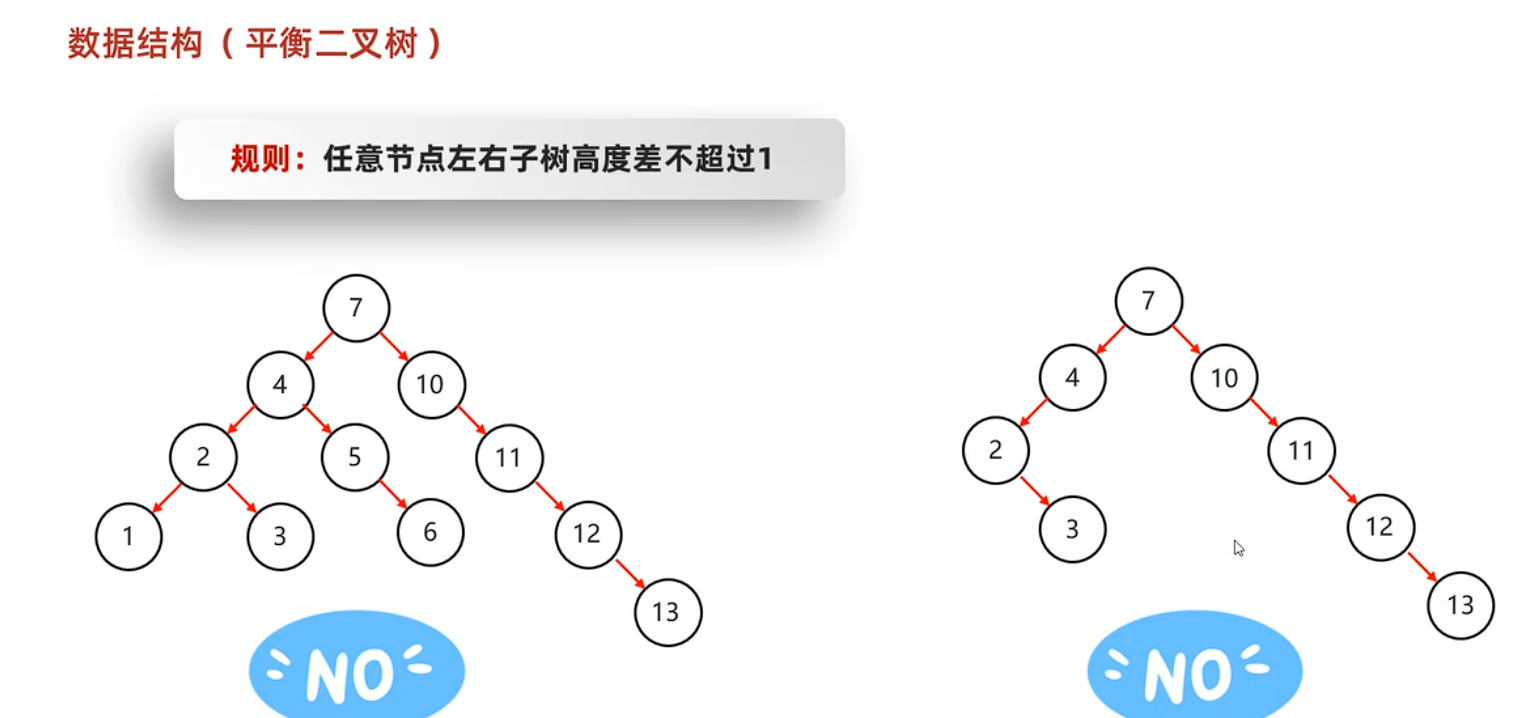
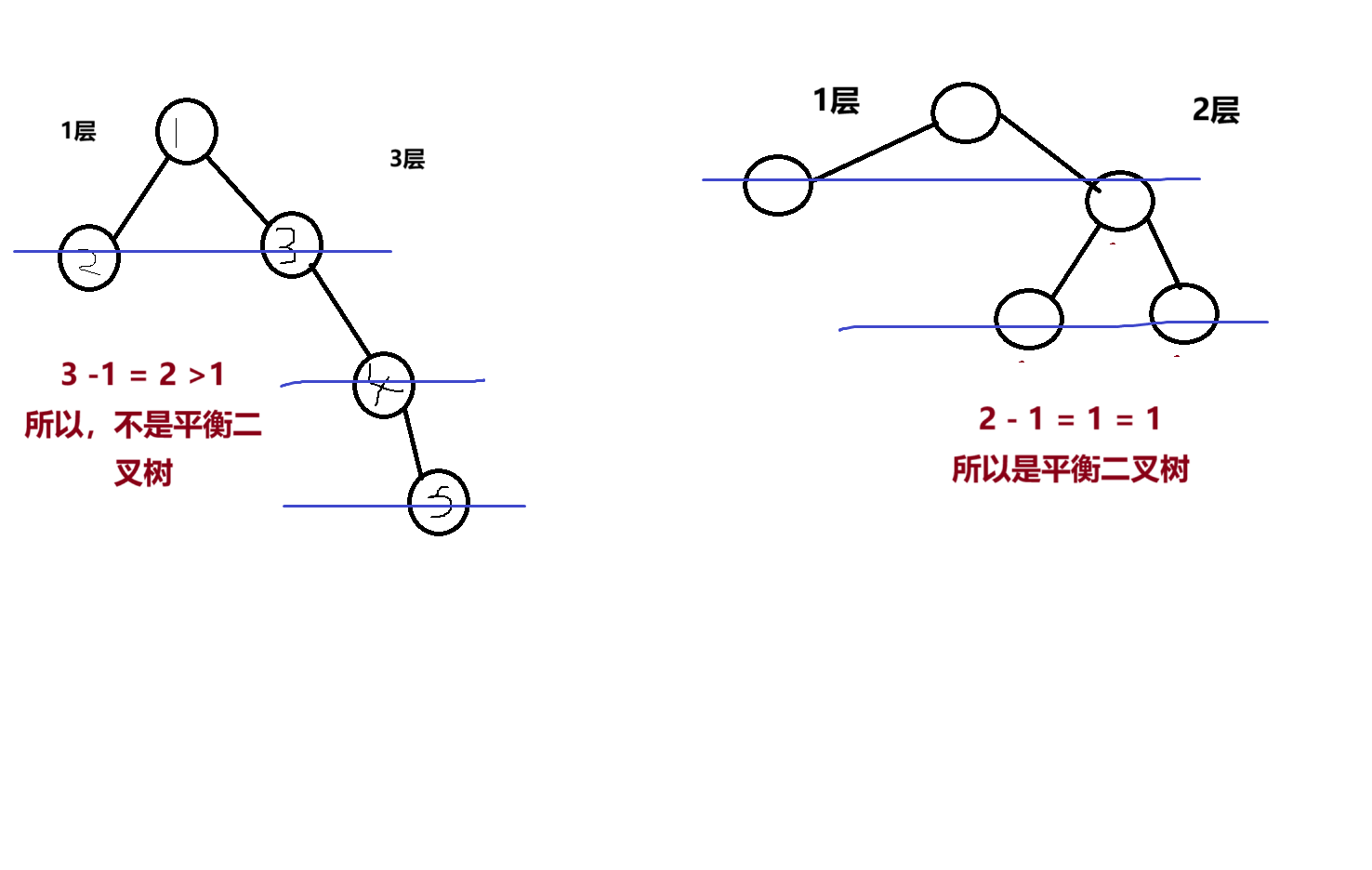
当插入或删除节点后,若某节点的平衡因子绝对值 > 1(失衡),需要通过「旋转」调整结构,恢复平衡。旋转的本质是通过调整节点的父子关系,降低树的高度,常见旋转分为 4 种场景:
1. 左旋(Left Rotation)
适用场景:右子树过深(如 RR 型失衡)。
操作步骤(以节点 X 为失衡点):
- 让 X 的右子节点 Y 成为新的父节点;
- X 的右子树更新为 Y 的左子树;
- Y 的左子树更新为 X;
- 原 Y 的父节点指向新根 Y。
// 左旋前(X失衡,右子树Y过深) X \ Y / \ A B // 左旋后(Y成为新根,X成为Y的左子树) Y / \ X B \ A 2. 右旋(Right Rotation)
适用场景:左子树过深(如 LL 型失衡)。
操作步骤(以节点 X 为失衡点):
- 让 X 的左子节点 Y 成为新的父节点;
- X 的左子树更新为 Y 的右子树;
- Y 的右子树更新为 X;
- 原 Y 的父节点指向新根 Y。
// 右旋前(X失衡,左子树Y过深) X / Y / \ A B // 右旋后(Y成为新根,X成为Y的右子树) Y / \ A X / B 3. 先左旋后右旋(LR 型)
适用场景:左子树的右子树过深(左 - 右结构导致失衡)。
操作步骤:
- 先对失衡节点的左子节点(Y)做左旋,将结构转为 LL 型;
- 再对原失衡节点(X)做右旋,恢复平衡。
// 失衡前(X的左子树Y的右子树Z过深) X / Y \ Z // 第一步:对Y左旋(转为LL型) X / Z / Y // 第二步:对X右旋(恢复平衡) Z / \ Y X 4. 先右旋后左旋(RL 型)
适用场景:右子树的左子树过深(右 - 左结构导致失衡)。
操作步骤:
- 先对失衡节点的右子节点(Y)做右旋,将结构转为 RR 型;
- 再对原失衡节点(X)做左旋,恢复平衡。
// 失衡前(X的右子树Y的左子树Z过深)
X \ Y /
Z // 第一步:对Y右旋(转为RR型)
X \ Z \ Y // 第二步:对X左旋(恢复平衡) Z / \ X Y 5、另一种技法

1、左左
即在节点的左子树的左节点添加新的节点,从添加的地方开始算是否违反规则,如在某节点违反,就在此节点进行一次右旋
2、左右
下面的都是将上面的词语换好就行,再去对照表格
3、右右
4、右左
三、红黑树的旋转
1、概念
红黑树也是一种「自平衡二叉查找树」,但它的平衡不是通过「平衡因子」,而是通过 5 条颜色规则(见前文)。旋转是红黑树维护规则的核心操作之一,旋转本身和 AVL 树的左旋 / 右旋完全相同,但触发旋转的条件和目的不同。
它通过一系列规则来维持树的平衡:
- 节点颜色:每个节点不是红色就是黑色
- 根节点:根节点必须是黑色
- 叶节点:所有叶节点(NIL 节点)都是黑色
- 红色节点的子节点:如果一个节点是红色,则它的子节点必须是黑色
- 路径一致性:从任一节点到其所有后代叶节点的路径包含相同数量的黑色节点
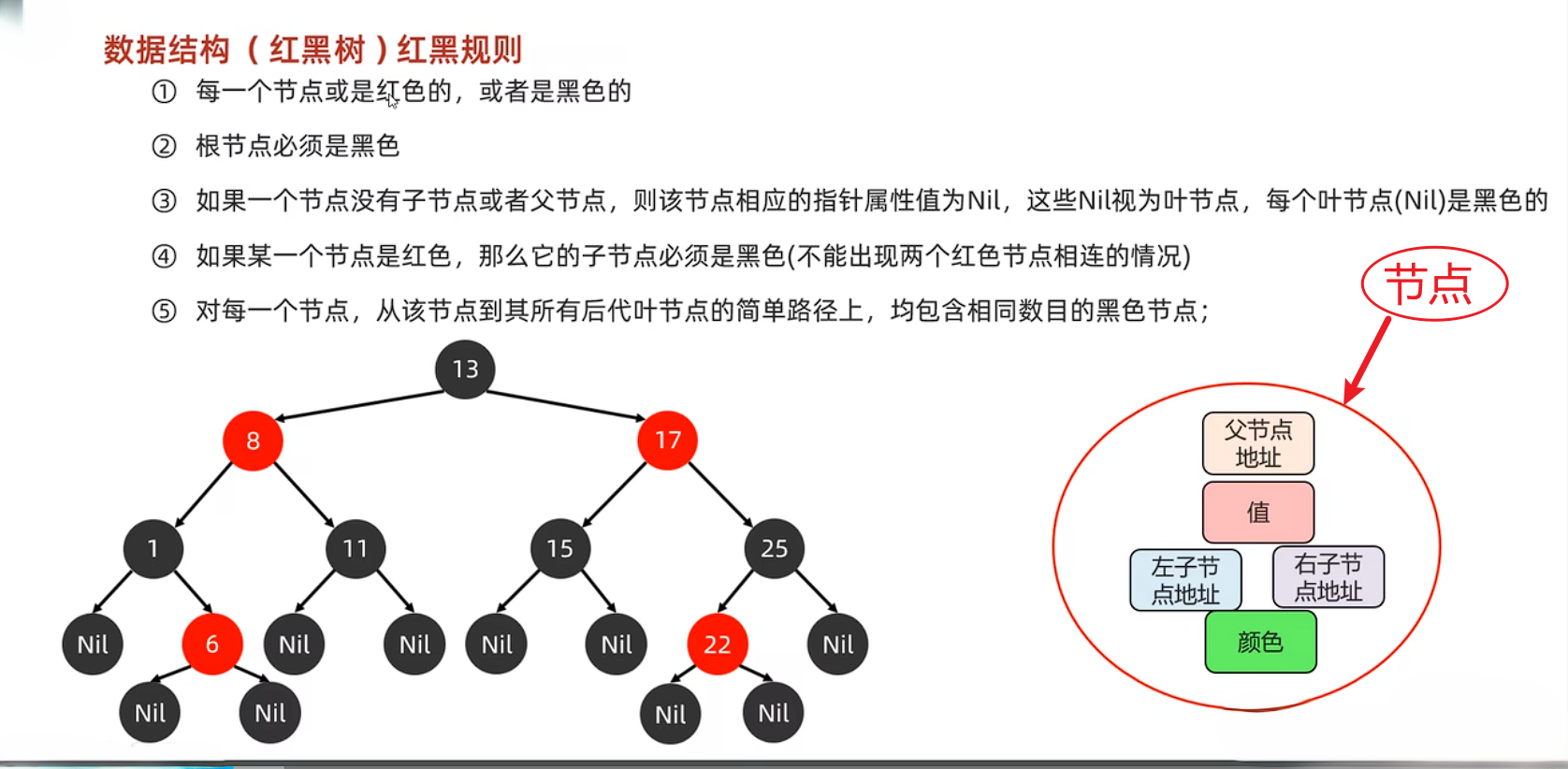
2、插入规则:
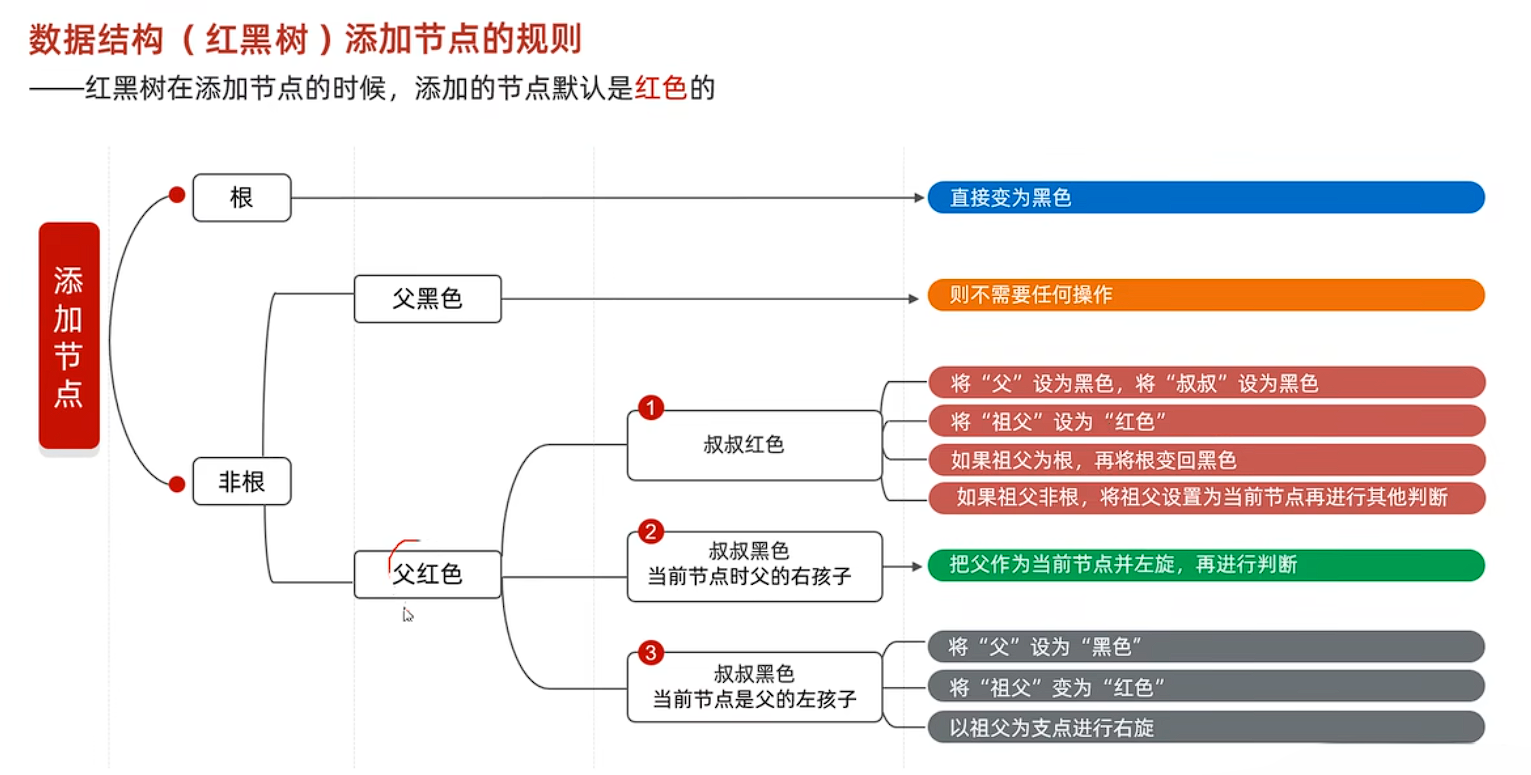
举例:
假设插入一个红色节点(红黑树新节点默认红色),若其父节点也是红色(违反规则 4:红色节点的子节点必须是黑色),且叔叔节点(父节点的兄弟)是黑色,则需要旋转:
场景 1:
父节点是左子节点,且新节点是父节点的左子节点(LL 型)
- 问题:父节点(红)和新节点(红)连续,叔叔节点(黑);
- 操作:对祖父节点右旋,同时交换父节点和祖父节点的颜色(父节点变黑,祖父节点变红)。
// 旋转前(违反规则4) 祖父(黑) / 父(红) /
新节点(红)
(叔叔节点为黑) // 右旋后 + 变色 父(黑) / \
新节点(红) 祖父(红) 场景 2:
父节点是右子节点,且新节点是父节点的右子节点(RR 型)
- 问题:父节点(红)和新节点(红)连续,叔叔节点(黑);
- 操作:对祖父节点左旋,同时交换父节点和祖父节点的颜色(父节点变黑,祖父节点变红)。
// 旋转前(违反规则4)
祖父(黑) \ 父(红) \ 新节点(红)
(叔叔节点为黑) // 左旋后 + 变色 父(黑) / \
祖父(红) 新节点(红) 场景 3:
父节点是左子节点,新节点是父节点的右子节点(LR 型)
- 问题:父节点(红)的右子节点(新节点,红),叔叔节点(黑);
- 操作:先对父节点左旋(转为 LL 型),再对祖父节点右旋,最后变色。
祖父(黑)/父节点(红) ← 父节点是祖父的左子节点\新节点(红) ← 新节点是父的右子节点
(叔叔节点为黑色或NIL)//对父节点做左旋(转为 LL 型)祖父(黑)/新节点(红) ← 左旋后,新节点成为父节点的父节点/父节点(红) ← 原父节点成为新节点的左子节点
(叔叔节点仍为黑色或NIL)//对祖父节点做右旋 + 变色新节点(黑) ← 新节点成为新的根,颜色变为黑色/ \
父节点(红) 祖父(红) ← 原父节点和祖父节点变为红色场景 4:
父节点是右子节点,新节点是父节点的左子节点(RL 型)
- 问题:父节点(红)的左子节点(新节点,红),叔叔节点(黑);
- 操作:先对父节点右旋(转为 RR 型),再对祖父节点左旋,最后变色
//初始状态(违反规则:连续两个红色节点)祖父(黑)\父节点(红) ← 父节点是祖父的右子节点/新节点(红) ← 新节点是父的左子节点
(叔叔节点为黑色或NIL)//对父节点做右旋(转为 RR 型)祖父(黑)\新节点(红) ← 右旋后,新节点成为父节点的父节点\父节点(红) ← 原父节点成为新节点的右子节点
(叔叔节点仍为黑色或NIL)//对祖父节点做左旋 + 变色新节点(黑) ← 新节点成为新的根,颜色变为黑色/ \
祖父(红) 父节点(红) ← 原祖父和父节点变为红色