当前位置：首页 > news >正文

GEAR：一种高效的 KV Cache 压缩方法，用于几乎无损的大语言模型生成式推理

news 2025/8/7 9:54:51

温馨提示：
本篇文章已同步至"AI专题精讲" GEAR：一种高效的 KV Cache 压缩方法，用于几乎无损的大语言模型生成式推理

摘要

Key-value（KV）缓存已成为提升大语言模型（LLM）推理生成速度的事实标准技术。然而，随着序列长度的增加，缓存需求的不断增长使得LLM推理演变为一个受限于内存带宽的问题，显著限制了系统吞吐量。现有方法通常依赖于丢弃不重要的token或对条目进行分组量化。然而，这些方法在表示压缩矩阵时常常引入较大的近似误差。自回归解码过程进一步在每个步骤中累积误差，导致模型生成结果的严重偏离与性能下降。

为了解决这一问题，我们提出了GEAR，一个高效的误差降低框架，它在量化方案中引入两个误差缓解模块，在高压缩率下实现了近乎无损的性能。GEAR首先将幅值相近的大部分条目以超低精度进行量化，然后使用一个低秩矩阵来逼近量化误差，同时引入一个稀疏矩阵来修正由离群条目产生的个别误差。通过巧妙地整合这三种技术，GEAR能够充分释放它们的协同潜力。

实验表明，GEAR在2-bit压缩率下的准确率与FP16缓存几乎一致，在精度方面比当前最优方法（SOTA）最多提升了24.42%。此外，与采用FP16 KV缓存的LLM推理相比，GEAR可将峰值内存消耗降低最多2.39倍，带来 2.1×至5.07× 的吞吐率提升。我们的代码已在以下地址开源：https://github.com/HaoKang-Timmy/GEAR

1 引言

自回归的大语言模型（LLMs）（Brown et al., 2020b；Zhang et al., 2022；Touvron et al., 2023a,b）在自然语言处理（NLP）和人工智能（AI）（Vaswani et al., 2017；Brown et al., 2020a；OpenAI, 2023）领域取得了重要突破，在内容创作、对话系统等广泛应用场景中展现出卓越的性能（Yuan et al., 2022；Thoppilan et al., 2022；Wei et al., 2022）。在LLM的生成式推理服务中，KV缓存机制已成为常规做法。它缓存此前注意力计算中得到的Key/Value张量，并在生成下一个token时复用这些缓存（Pope et al., 2022），从而避免重复计算，大幅提升生成速度。

在这里插入图片描述

尽管KV缓存在推理中至关重要，但其内存消耗却随着模型规模和序列长度迅速增长，极大地限制了系统吞吐。例如，在一个参数规模为300亿的大模型中，当输入长度为1024、batch size为128时，其生成的KV缓存可能会占用多达 180GB 的内存（Zhang et al., 2023b）。为了缓解GPU有限显存带来的压力，推理系统通常采用缓存卸载（offloading）策略（Aminabadi et al., 2022；Sheng et al., 2023），即将KV缓存转移至CPU内存或NVMe存储。然而，这种方式仍然会带来不可忽视的开销，因为许多设备中GPU与CPU之间的PCIe带宽有限。因此，降低KV缓存作为推理瓶颈的内存占用变得尤为关键。

为了解决这一问题，研究者提出了基于token丢弃的压缩方法，以在保留生成性能的同时减少缓存大小（Zhang et al., 2023b；Liu et al., 2023；Ge et al., 2023）。这些方法利用注意力得分中的稀疏性，从KV缓存中剔除不重要token的embedding，仅保留被频繁关注的token。例如，H2O（Zhang et al., 2023b）通过累计注意力得分评估token重要性，并移除得分较低的token以减少缓存大小。

此外，量化也是一种被广泛采用的压缩策略，它通过将全精度张量值映射为离散级别并以较低精度（如INT4或INT8）进行存储，从而压缩KV缓存（Zafrir et al., 2019；Dettmers et al., 2022；Sheng et al., 2023）。例如，FlexGen（Sheng et al., 2023）采用了细粒度的组内非对称量化：将每个token的KV条目分组，g个相邻条目组成一组，然后对该组张量进行量化。两项最新工作（Liu et al., 2024；Hooper et al., 2024）进一步研究了KV条目的分布，提出对Key缓存按通道量化、对Value缓存按token量化，从而实现更高比例的缓存压缩。

这些现有方法在多个自然语言理解任务（如多项选择问答、文本分类或简单摘要）中能够在低精度下实现接近无损的表现（Zhang et al., 2023b；Liu et al., 2024）。然而，当它们被应用于生成更长文本或涉及推理等更复杂的生成任务时，性能出现了明显下降，如数学问题求解（Cobbe et al., 2021）和链式思维（CoT）推理（Wei et al., 2023）。当压缩率较高时（如4-bit/2-bit量化，或丢弃超过50%的token（Ge et al., 2023）），上述方法的性能劣化尤为明显。这种现象可以归因于它们引入了不可忽略的近似误差，即原始KV与压缩KV之间的差异。

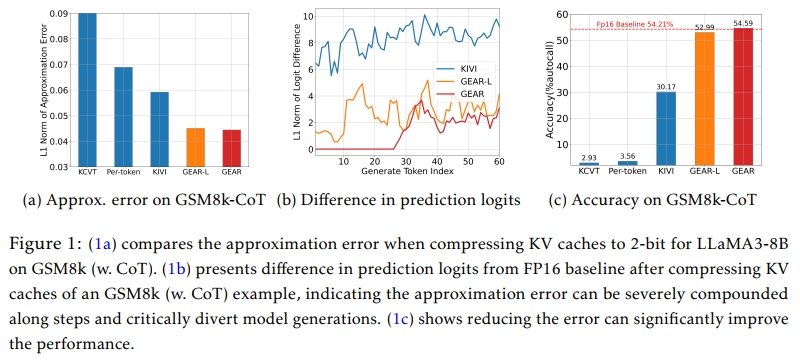
对于简单任务，模型只需生成少量token，所需的关键信息往往可由少数重要上下文token推断得到，因此，即使存在较大的近似误差，也不会严重影响生成目标token。而对于复杂任务，模型需要基于密集相关的提示信息生成较长文本（如CoT推理），而自回归解码机制会在每一步累积误差，哪怕是较小的误差也会逐步放大，严重影响后续的生成过程。例如，图1展示了各方法在GSM8k任务上的近似误差，并揭示了token生成偏离的累积效应，导致准确率大幅下降。因此，关键问题在于这些方法在高压缩率下的近似误差过大。

为了解决这一问题，我们提出 GEAR（GEnerative Inference with Approximation Error Reduction），这是一个高效的误差缓解框架，它在现有KV缓存量化方案的基础上引入两种误差缓解机制，并通过巧妙整合最大化发挥其潜力。总体上，GEAR包括以下三个组成部分用于分解KV矩阵：

量化主干部分：我们首先采用已有的量化方法，将绝大多数（如98%）幅值相近的条目以超低精度进行高效量化；
低秩矩阵补偿：我们引入一个低秩矩阵，用于高效逼近上述量化残差；
稀疏矩阵修正：我们使用一个稀疏矩阵，仅包含极少数大幅值条目，用以修正由这些离群值引起的个体误差。

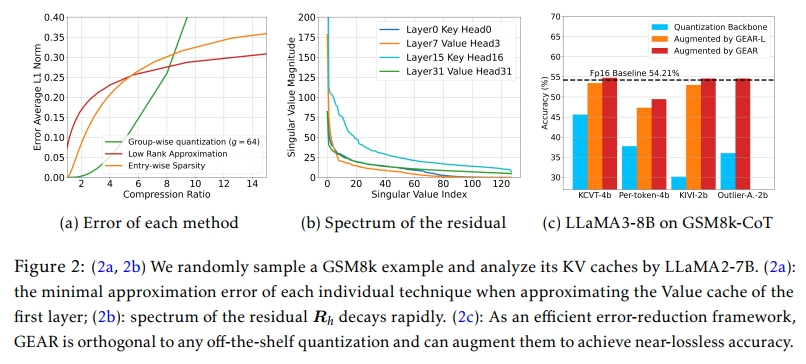
这种复合近似方式将近似误差中可协同部分与非协同部分有效解耦：低秩矩阵捕捉量化误差的主要协同基底，而稀疏矩阵则纠正了存在于个别异常条目中的非协同误差。我们在第4.2节的实验证据中表明，这两个轻量级组件几乎不会引入额外内存和计算开销，具备极高效率。因此，GEAR能够在高压缩率下高效减少近似误差，在复杂和简单任务中都能获得优越的性能表现，且具备良好的即插即用性。我们发现：同时使用稀疏与低秩组件是GEAR实现最优性能的关键，突显了它们的互补性。值得注意的是，对于偏向效率优先的场景，仅使用低秩近似组件也能有效降低误差，同时带来显著的效率与性能提升，我们将该精简版本命名为 GEAR-L。

此外，我们为GEAR设计了一种 流式缓存策略 以进一步提高推理效率。具体来说，在生成长序列时，我们将新生成token的KV向量临时保存在一个小缓存中（例如，缓存大小nb = 20）。当缓存达到容量后，GEAR每nb步对KV缓存进行一次压缩，从而以非常小的内存代价显著提升推理速度。

为了进一步降低开销，我们还提供了一个GPU友好的核函数实现，它结合流式机制与量化优化，大幅提升推理吞吐率。

我们在多种任务和模型上开展实验，验证GEAR的有效性。具体而言，我们在 数学推理任务（GSM8k（Cobbe et al., 2021）、AQuA（Ling et al., 2017））、符号推理任务（BigBench Hard（Suzgun et al., 2022））、长上下文理解任务（LongBench（Bai et al., 2023））上，评估GEAR在 LLaMA2-7B/13B（Touvron et al., 2023b）、Mistral-7B（Jiang et al., 2023）和LLaMA3-8B（Meta, 2024）等模型上的压缩效果。

结果表明，GEAR在高压缩率（如2-bit精度）下始终优于各类基线方法。例如，在将KV缓存压缩至2-bit时，GEAR在多个模型和数据集上的平均准确率提升达 14.95%，远超表现最好的基线方案。关于推理效率，与FP16缓存相比，GEAR可将峰值显存占用降低最多2.39倍，实现 2.10×至5.07× 的吞吐率提升。

2 背景

多头注意力机制（Multi-head attention）
一个典型的transformer模型由 $L$ 个堆叠的层组成，每一层包含两个子模块：一个多头注意力机制（MHA）和一个前馈神经网络（FFN）。给定输入的token embedding为 $\in \mathbb{R}^{n \times d}$ ，MHA会在 $H$ 个注意力头上并行地执行注意力函数：
$MHA(X)=Concat(H(1),…,H(H))Wo,H(i)=Softmax(Q(i)K(i)⊤dH)V(i)(1)\text{MHA}(X) = \text{Concat}(H^{(1)}, \ldots, H^{(H)}) W_o, \quad H^{(i)} = \text{Softmax}\left(\frac{Q^{(i)} {K^{(i)}}^\top}{\sqrt{d_H}}\right) V^{(i)} \quad(1)$

其中， $Q^{(i)} = X W_{qi}, K^{(i)} = X W_{ki}, V^{(i)} = X W_{vi}$ 分别是Query/Key/Value矩阵， $\in \mathbb { R } ^ { d \times d _ { H } }$ 是第 $i$ 个头的投影矩阵， $d_H$ 通常设为 $d / H$ 。

预填充与解码（Prefill and decoding）
假设模型需要生成 $n_g$ 个token。在第一个生成步骤中，输入token $X0∈Rn×dX_0 \in \mathbb{R}^{n \times d}$ 会被预填充（prefill）。随后，所有层和所有注意力头上的 $K^{(i)}$ 和 $V^{(i)}$ 都会被缓存下来，作为后续生成的初始KV缓存：
$K0=Concat(K(1),…,K(H)),V0=Concat(V(1),…,V(H)),K0,V0∈Rn×dK_0 = \text{Concat}(K^{(1)}, \ldots, K^{(H)}), \quad V_0 = \text{Concat}(V^{(1)}, \ldots, V^{(H)}), \quad K_0, V_0 \in \mathbb{R}^{n \times d}$

在自回归解码（autoregressive decoding）的每一步 $t$ （ $\leq t \leq n_g$ ）中，模型基于输入和历史生成的token预测下一个token $x_t$ 。在接下来的步骤中，MHA只需为新生成的token $x_t$ 计算其Query/Key/Value向量（ $qt,kt,vt∈Rdq_t, k_t, v_t \in \mathbb{R}^d$ ），并将 $k_t, v_t$ 添加到KV缓存中：

$Kt=Kt−1∥kt,Vt=Vt−1∥vtK_t = K_{t-1} \| k_t, \quad V_t = V_{t-1} \| v_t$

然后，注意力操作（公式(1)）只在 $q_t$ 与 $K_t, V_t$ 之间进行。

Group-wise Quantization
Group-wise quantization 被广泛用于压缩 KV cache（Sheng et al., 2023；Liu et al., 2024；Hooper et al., 2024）。给定一个全精度的张量 $\in \mathbb{R}^{n \times d}$ ，最基本的方法是按照token将条目分组，即将每个token的 $g$ 个连续条目放入一个组。例如，第 $i$ 个分组 $\mathcal { G } _ { i } }$ 包含的条目索引为 $Gi={(ti,ci),…,(ti,ci+g)}.\mathcal { G } _ { i } = \{ ( t _ { i } , c _ { i } ) , \ldots , ( t _ { i } , c _ { i } + g ) \} \, .$ 其中 $t_i, c_i)$ 是第 $i$ 组的起始索引， $g$ 是组的大小。然后，对 $X$ 进行 group-wise 量化： $X^=Quant⁡b,g(per−token)\widehat { X } = \operatorname { Q u a n t } _ { b , g } ^ { ( \mathrm { p e r - t o k e n } ) }$ ，其中
$Quantb,g(per⋅token)(X)Gi=[(XGi−min⁡XGi)/Δi],Δi=(max⁡XGi−min⁡XGi)/(2b−1)（2）\mathrm { Q u a n t } _ { b , g } ^ { ( \mathrm { p e r } \cdot \mathrm { t o k e n } ) } ( X ) _ { \mathcal { G } _ { i } } = \left[ ( X _ { \mathcal { G } _ { i } } - \operatorname* { m i n } X _ { \mathcal { G } _ { i } } ) / \Delta _ { i } \right] , \: \Delta _ { i } = ( \operatorname* { m a x } X _ { \mathcal { G } _ { i } } - \operatorname* { m i n } X _ { \mathcal { G } _ { i } } ) / ( 2 ^ { b } - 1 )\quad（2）$
其中 $b$ 是位宽， $X^\widehat { X }$ 是 $b$ 位精度下的量化张量， $⌈⋅⌋\lceil \cdot \rfloor$ 是取整函数。 $Δi\Delta_i$ 和 $min X_{G_i}$ 分别是第 $i$ 组的缩放因子和零点。两项同期工作（KIVI Liu et al. (2024) 和 KVQuant Hooper et al. (2024)）研究了 KV cache 的条目分布，并发现，在 Key cache 中，一些固定的通道呈现出非常大的幅值。为了将量化误差限制在各个独立通道中而不影响其他通道，它们提出对 Key cache 进行 per-channel 量化，而对 Value cache 进行 per-token 量化，从而实现了当前最先进的 2-bit 压缩。

直观上，更细粒度的分组（如 KIVI Liu et al. (2024) 中设置的 $g = 64$ ）会带来更精确的近似，从而获得更好的性能。然而，小组大小会带来相当大的内存开销，因为每组都需存储以全精度表示的缩放因子和零点。同时，用于 per-channel 量化的细粒度分组也意味着必须将一部分 KV token 保留为全精度，直到它们形成一个完整的组（Liu et al. (2024)）。因此，这部分全精度内容的剩余长度必须设为组大小的倍数（例如 KIVI 设置为 128），这进一步带来额外的显著开销。为了在最小化开销的同时利用当前最先进的量化方案，我们选择对 Key 进行 per-channel、对 Value 进行 per-token 的量化，同时不使用细粒度分组，作为轻量化的量化主干。我们称之为 KCVT，它是 KIVI 的一个变体，采用粗粒度的 per-vector 分组方式：将每个通道的所有 Key 条目组成一个大小为 $n$ 的组，将每个 token 的所有 Value 条目组成一个大小为 $d$ 的组，这样可以显著减少缩放因子和零点的存储开销。
在这里插入图片描述

3 GEAR 框架

GEAR 框架由三个重要组件组成，用于分解和压缩 KV cache 矩阵：(i) 一个量化矩阵 $D^\widehat { \cal D }$ ，作为压缩主干；(ii) 一个低秩矩阵 $L$ ，用于近似量化残差；(iii) 一个稀疏矩阵 $S$ ，用于捕捉个别异常值。如第 1 节所述，近似误差在决定模型性能方面起着关键作用。因此，给定张量 $\in \{ K _ { t } , V _ { t } \}$ ，我们的目标是最小化其压缩近似的误差。一个简单的策略是分别采用这三种压缩方法，并通过最小化与 $X$ 的距离来进行近似。例如，可以通过 $X$ 的前几个奇异值/奇异向量构建 $L$ ，或使用幅度最大的条目组成 $S$ 。

然而，如图 2a 所示，仅依赖这三种方法中的任意一种都无法在高压缩率下实现低误差，因为它们在高压缩率条件下都会引入显著的误差。此外，$\widehat { D } $、$ L$ $S$ 在矩阵近似中扮演不同角色，分别捕捉 $X$ 的不同组成部分。这些动因促使我们探索将三种技术融合的可能性，以利用它们各自的优势并挖掘它们之间的协同潜力。为此，我们的目标转化为最小化以下近似误差：
$min⁡D^,L,S∥X−D^−L−S∥F(3)\operatorname* { m i n } _ { \widehat { D } , L , S } \left\| X - \widehat { D } - L - S \right\| _ { \mathrm { F } } \quad(3)$