碰撞问题的分析

碰撞问题

问题的假设

• 瞬时性假设：碰撞持续时间极短（微秒至毫秒级），远小于宏观运动时间，非碰撞外力（重力、摩擦力等）的冲量可忽略，仅考虑碰撞力冲量对动量的影响。

• 外力主导性忽略假设：碰撞瞬间，碰撞力远大于其他外力，外力对物体运动状态的影响可忽略，动量变化仅由碰撞力决定。

• 碰撞力方向假设：碰撞力沿两物体接触点的公法线方向（垂直于接触表面），切向力通常单独分析或忽略（除非考虑摩擦滑动）。

• 冲量主导假设：碰撞力为冲击力，大小随时间急剧变化，分析中更关注其冲量（力对时间的积分），因冲量直接决定动量变化（动量定理：冲量=动量变化量）。

• 力与变形关联假设：弹性碰撞中，碰撞力与碰撞方向的相对压缩量成正比，压缩与恢复阶段力-变形关系对称；非弹性碰撞中，恢复阶段的力小于压缩阶段同变形量下的力，导致能量耗散。

• 刚性体假设：碰撞物体为绝对刚性体（或变形可忽略），不发生形变，仅整体平移或转动，简化对内部应力和形变的分析。

• 均质与形状简化假设：物体质量分布均匀，形状简化为质点、刚体（小球、滑块等），忽略不规则形状对碰撞的影响。

• 微小位移假设：碰撞中物体的位移远小于自身尺寸和碰撞前运动距离，可认为位置不变，仅速度（或角速度）突变。

• 相对位移聚焦假设：重点分析两物体沿碰撞方向的相对位移（压缩阶段靠近、恢复阶段分离），最大相对压缩量对应碰撞力峰值时刻。

• 动量守恒假设：无外力（或外力可忽略）时，碰撞系统总动量守恒（沿碰撞方向或动量矢量守恒）。

• 能量损失假设：

  • 弹性碰撞：无能量损失（动能守恒），仅动量和动能在物体间转移；
  • 非弹性碰撞：存在能量损失（转化为热能、形变能等），通过恢复系数（分离速度与靠近速度的比值）描述，恢复系数=1为完全弹性，=0为完全非弹性。

碰撞的分类

碰撞可以按作用力与速度的方向进行分类如图，若碰撞力作用线通过俩个物体的质心，称为对心碰撞，否则称为偏心碰撞。

若碰撞时两物体各自质心的速度均沿公法线，则称正碰撞，否则称为斜碰撞。

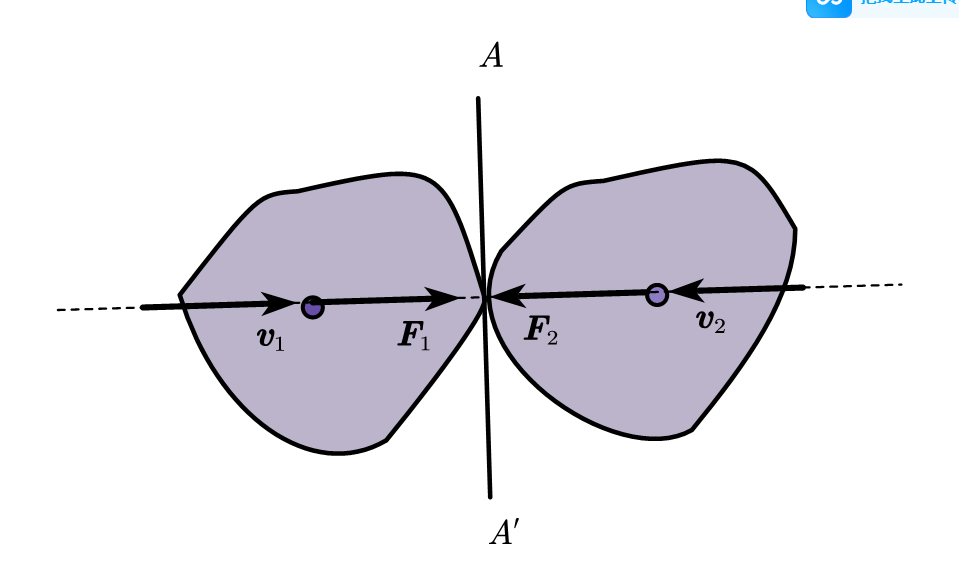
两个物体相撞时，按其接触处有无摩擦，还可以分为光滑碰撞与非光滑碰撞。

两物体碰撞时，可以按物体碰撞前后变形恢复程度(能量损失情况)，分为完全弹性碰撞、弹性碰撞和塑性碰撞。

用于碰撞构成的基本定理

一般采用动量定理和动量矩定理的积分形式来确定力的作用关系与运动变化的关系。

1.质点系的碰撞方程

① 质点系的冲量定理：质点系所受外力的总冲量等于质点系总动量的增量，即作用于质点系的所有外力在某一时间间隔内的冲量矢量和，等于该质点系在同一时间间隔内总动量的变化量。
$$m_c{\mathbf{v}}_c^{\prime }-m_c{\mathbf{v}}_c=\sum _i{\mathbf{I}}_i^{(e)}$$
其中，$m_c$为质点系的总质量（质心质量），${\mathbf{v}}_c^{\prime }$为碰撞后质心的速度，${\mathbf{v}}_c$为碰撞前质心的速度，${\mathbf{I}}_i^{(e)}$为第$i$个质点所受外碰撞冲量（外力在碰撞时间内的冲量）。该定理表明，质点系总动量的改变仅由外力冲量决定，内力冲量不会影响总动量。

证明

对于碰撞的质点系，作用在第 $i$ 个质点上的碰撞冲量可分为外碰撞冲量 ${\mathbf{I}}_i^{(e)}$ 和内碰撞冲量 ${\mathbf{I}}_i^{(i)}$，按照上式有
$$m_i{\mathbf{v}}_i^{\prime }-m_i{\mathbf{v}}_i={\mathbf{I}}_i^{(e)}+{\mathbf{I}}_i^{(i)}$$
设质点系有 $n $ 个质点，对于每个质点都可列出如上的方程，将 $n $ 个方程相加，得
$$\sum _{i=1}^n{m}_i{\mathbf{v}}_i^{\prime }-\sum _{i=1}^n{m}_i{\mathbf{v}}_i=\sum _{i=1}^n{\mathbf{I}}_i^{(e)}+\sum _{i=1}^n{\mathbf{I}}_i^{(i)}$$

因为内碰撞冲量总是大小相等，方向相反，成对地存在，因此 $\sum_{i = 1}^{n} \boldsymbol{I}_{i}^{(i)} = \boldsymbol{0} $，于是得
$$\sum _{i=1}^n{m}_i{\mathbf{v}}_i^{\prime }-\sum _{i=1}^n{m}_i{\mathbf{v}}_i=\sum _{i=1}^n{\mathbf{I}}_i^{(e)}$$

得到：
$$m_c{\mathbf{v}}_c^{\prime }-m_c{\mathbf{v}}_c=\sum _i{\mathbf{I}}_i^{(e)}$$

② 质点系的冲量矩定理：质点系所受外力对某固定点的总冲量矩等于质点系对该固定点的总角动量的增量，即作用于质点系的所有外力在某一时间间隔内对固定点的冲量矩矢量和，等于该质点系在同一时间间隔内对该固定点总角动量的变化量。
$${\mathbf{L}}_{O2}-{\mathbf{L}}_{O1}=\sum _i{\mathbf{M}}_O({\mathbf{I}}_i^{(e)})$$
其中，${\mathbf{L}}_{O2}$为质点系在碰撞后对固定点$O$的总角动量，${\mathbf{L}}_{O1}$为碰撞前对固定点$O$的总角动量，${\mathbf{M}}_O({\mathbf{I}}_i^{(e)})$为第$i$个质点所受外碰撞冲量${\mathbf{I}}_i^{(e)}$对固定点$O$的冲量矩（冲量与力的作用点到$O$点矢径的叉积）。该定理表明，质点系对固定点的角动量变化仅由外力冲量矩决定，内力冲量矩不会改变总角动量。

证明

质点系动量矩定理的一般表达式为微分形式，即
$$\frac{\mathrm{d}}{\mathrm{d}t}{\mathbf{L}}_O=\sum _{i=1}^n{\mathbf{M}}_O({\mathbf{F}}_i^{(e)})=\sum _{i=1}^n({\mathbf{r}}_i\times {\mathbf{F}}_i^{(e)})$$
式中，${\mathbf{L}}_O$为质点系对于定点$O$的动量矩矢，${\sum }_{i=1}^n({\mathbf{r}}_i\times {\mathbf{F}}_i^{(e)})$为作用于质点系的外力对点$O$的主矩。
上式可写成
$$\mathrm{d}{\mathbf{L}}_O=\sum _{i=1}^n({\mathbf{r}}_i\times {\mathbf{F}}_i^{(e)})\mathrm{d}t=\sum _{i=1}^n({\mathbf{r}}_i\times \mathrm{d}{\mathbf{I}}_i^{(e)})$$ 对上式积分，得
$${\int }_{{\mathbf{L}}_{O1}}^{{\mathbf{L}}_{O2}}\mathrm{d}{\mathbf{L}}_O=\sum _{i=1}^n{\int }_0^t({\mathbf{r}}_i\times \mathrm{d}{\mathbf{I}}_i^{(e)})$$ 或 $${\mathbf{L}}_{O2}-{\mathbf{L}}_{O1}=\sum _{i=1}^n{\int }_0^t({\mathbf{r}}_i\times \mathrm{d}{\mathbf{I}}_i^{(e)})$$
一般情况下，上式中${\mathbf{r}}_i$是未知的变量，上式难以积分。但在碰撞过程中，按基本假设，各质点的位置都是不变的，因此碰撞力作用点的矢径${\mathbf{r}}_i$是个恒矢量，于是有
$${\mathbf{L}}_{O2}-{\mathbf{L}}_{O1}=\sum _{i=1}^n{\mathbf{r}}_i\times {\int }_0^t\mathrm{d}{\mathbf{I}}_i^{(e)}$$ 或 $${\mathbf{L}}_{O2}-{\mathbf{L}}_{O1}=\sum _{i=1}^n({\mathbf{r}}_i\times {\mathbf{I}}_i^{(e)})=\sum _{i=1}^n{\mathbf{M}}_O({\mathbf{I}}_i^{(e)})$$
式中，${\mathbf{L}}_{O1}$和${\mathbf{L}}_{O2}$分别是碰撞开始和结束时质点系对点$O$的动量矩，${\mathbf{I}}_i^{(e)}$是外碰撞冲量。

③刚体平面运动碰撞方程
$$\{\begin{array}{l}{m}_c{\mathbf{v}}_c^{\prime }-m_c{\mathbf{v}}_c={\sum }_i{\mathbf{I}}_i^{(e)}\\ {\mathbf{L}}_{C2}-{\mathbf{L}}_{C1}={\sum }_i{\mathbf{M}}_C({\mathbf{I}}_i^{(e)})\end{array}$$
对于平行于其质量对称平面的平面运动刚体：
$$\{\begin{array}{l}{m}_c{\mathbf{v}}_c^{\prime }-m_c{\mathbf{v}}_c={\sum }_i{\mathbf{I}}_i^{(e)}\\ J_c{\omega }_2-J_c{\omega }_1={\sum }_i{M}_C({\mathbf{I}}_i^{(e)})\end{array}$$

对固定面的碰撞

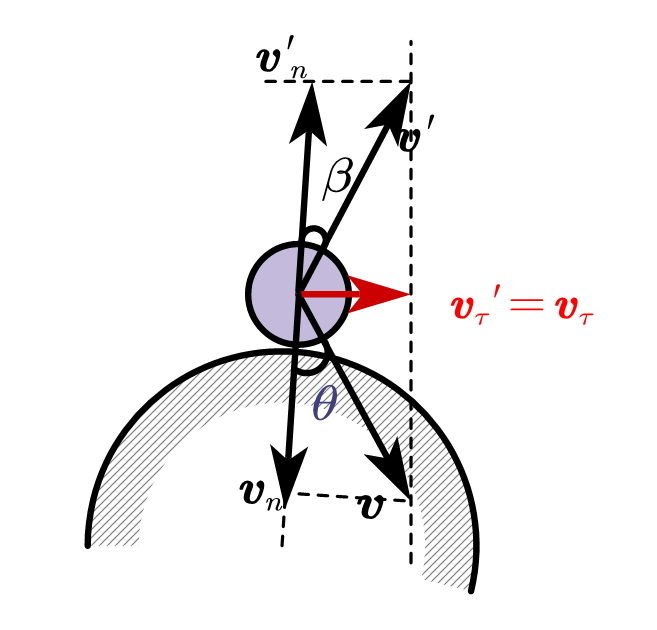
小球与固定面的斜碰撞（不计摩擦）
如果小球与固定面碰撞，碰撞开始瞬时的速度 $v$ 与接触点法线的夹角为 $\theta$，碰撞结束时返跳速度 $v^{\prime }$ 与法线的夹角为 $\beta$（如图 3 - 4 所示，此为斜碰撞场景 ）。

设不计摩擦，两物体只在法线方向发生碰撞，此时定义恢复因数为：
$$e=\left|\frac{v_n^{\prime }}{v_n}\right|$$
式中，$v_n^{\prime }$ 和 $v_n$ 分别是速度 $v^{\prime }$ 和 $v$ 在法线方向的投影。

由于不计摩擦，$v^{\prime }$ 和 $v$ 在切线方向的投影相等，由图可见：
$$\left|v_n^{\prime }\right|\tan \beta =\left|v_n\right|\tan \theta$$

于是，有：
$$e=\left|\frac{v_n^{\prime }}{v_n}\right|=\frac{\tan \theta }{\tan \beta }$$

对于实际材料有 $e<1$，由上式可见，当碰撞物体表面光滑时，应有 $\beta >\theta$。

一般情况（两运动物体斜碰撞，不计摩擦）

在不考虑摩擦的一般情况下，碰撞前后的两个物体都在运动，此时恢复因数定义为：
$$e=\left|\frac{v_r^{\prime n}}{v_r^n}\right|$$
式中，$v_r^{\prime n}$ 和 $v_r^n$ 分别为碰撞后和碰撞前两物体接触点沿接触面法线方向的相对速度。

碰撞冲量对绕定轴转动刚体的作用

定轴转动刚体所受到碰撞时角速度的变化

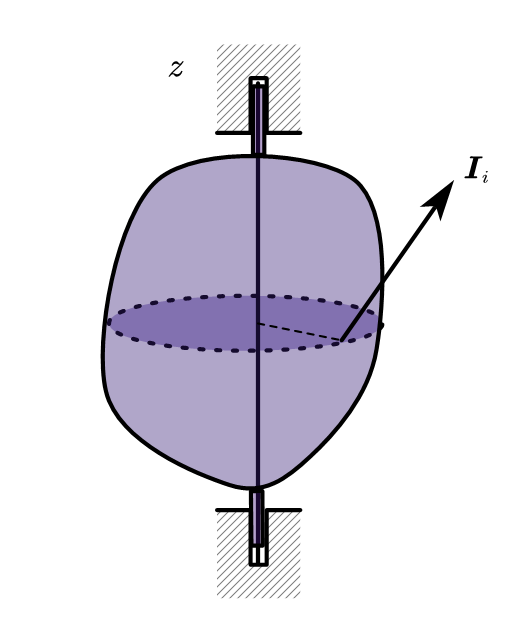
使用$z$轴的动量矩定理投影式：

$$J_z{\omega }_2-J_z{\omega }_1=\sum _i{M}_z({\mathbf{I}}_i^{(e)})$$

支座的反碰撞冲量与碰撞中心

设刚体有质量对称平面，且绕垂直于此对称平面的轴转动，并设图示平面图形为刚体质量对称平面，则刚体质心必在质量对称平面内。

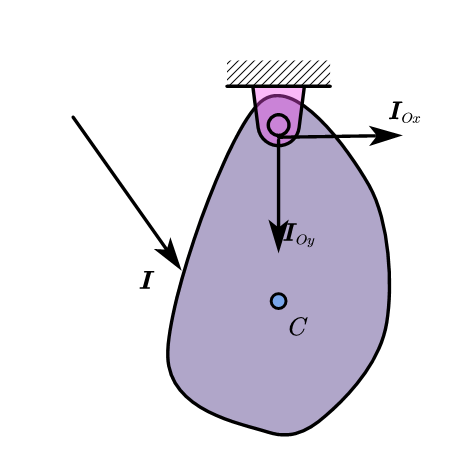
2. 支座的反碰撞冲量·撞击中心

绕定轴转动的刚体（如图 3-8 所示），受到外碰撞冲量 $I$ 作用时，轴承与轴间将发生碰撞。

设刚体有质量对称平面，且绕垂直于此对称平面的轴转动，图示平面图形是刚体的质量对称平面，则刚体的质心 $C$ 必在图面内。

取 $y$ 轴通过质心 $C$，$x$ 轴与 $y$ 轴垂直。

今有外碰撞冲量 $\mathbf{I}$ 作用在此对称平面内，求轴承 $O$ 的反碰撞冲量 ${\mathbf{I}}_{Ox}$ 和 ${\mathbf{I}}_{Oy}$。

应用冲量定理，有：
$$m{v}_{Cx}^{\prime }-m{v}_{Cx}=I_x+I_{Ox}$$
$$m{v}_{Cy}^{\prime }-m{v}_{Cy}=I_y+I_{Oy}$$

式中：

• $m$ 为刚体质心；
• $v_{Cx}、v_{Cx}^{\prime }$ 为碰撞前后质心速度沿 $x$ 轴的投影；
• $v_{Cy}、v_{Cy}^{\prime }$ 为碰撞前后质心速度沿 $y$ 轴的投影；
• $I_x、I_y$为外碰撞冲量$I$ 沿$x、y$轴的投影。

若图示位置是发生碰撞的位置，且轴承没有被撞坏，则碰撞前后质心在 $y$ 方向速度不变，即：
$$v_{Cy}^{\prime }=v_{Cy}=0$$

代入冲量定理公式，可得：
$$I_{Ox}=m(v_{Cx}^{\prime }-v_{Cx})-I_x$$
$$I_{Oy}=-I_y$$

由此可见，一般情况下，轴承处会因碰撞产生反碰撞冲量 。

应用于碰撞过程的拉格朗日方程

碰撞问题可用拉格朗日方程求解，对其时间域积分形式推导如下：
将式第二类拉格朗日方程两端对时间积分：
$${\int }_0^{\Delta t}\frac{\mathrm{d}}{\mathrm{d}t}\left(\frac{\partial T}{\partial {\dot{q}}_k}\right)\mathrm{d}t-{\int }_0^{\Delta t}\frac{\partial T}{\partial q_k}\mathrm{d}t={\int }_0^{\Delta t}{Q}_k\mathrm{d}t\text{\hspace{1em}(1)}$$
由于碰撞过程中质点速度有限、位置变化可忽略，当$\Delta t\to 0$时，$\frac{\partial T}{\partial q_k}$为有限值，故：
$${\int }_0^{\Delta t}\frac{\partial T}{\partial q_k}\mathrm{d}t\to 0$$
将其代入式$(1)$，并考虑碰撞前、后时刻（下标“1”“2” ），可得：
$${\left(\frac{\partial T}{\partial {\dot{q}}_k}\right)}_2-{\left(\frac{\partial T}{\partial {\dot{q}}_k}\right)}_1={\int }_0^{\Delta t}{Q}_k\mathrm{d}t\text{\hspace{1em}(2)}$$
令$I_k={\int }_0^{\Delta t}{Q}_k\mathrm{d}t$（对应第$k$个广义力的广义冲量），又因$\frac{\partial T}{\partial {\dot{q}}_k}=p_k$（与第$k$个广义坐标对应的广义动量 ），则动力学方程可写为：
$$p_{k2}-p_{k1}=I_k\text{\hspace{1em}(3)}$$
此式称为广义冲量定理 。

为计算广义冲量，对虚功原理表达式两端对时间积分：
$${\int }_0^{\Delta t}\delta W\mathrm{d}t={\int }_0^{\Delta t}\sum _{i=1}^N{\mathbf{F}}_i\cdot \delta {\mathbf{r}}_i\mathrm{d}t=\sum _{i=1}^N\left({\int }_0^{\Delta t}{\mathbf{F}}_i\mathrm{d}t\right)\cdot \delta {\mathbf{r}}_i=\sum _{i=1}^N{\mathbf{I}}_i\cdot \delta \mathbf{r}\text{\hspace{1em}(4)}$$

虚功的时间积分形式为：
$${\int }_0^{\Delta t}\delta W\mathrm{d}t={\int }_0^{\Delta t}\sum _{k=1}^N{Q}_k\delta q_k\mathrm{d}t=\sum _{k=1}^N\left({\int }_0^{\Delta t}{Q}_k\mathrm{d}t\right)\delta q_k=\sum _{k=1}^N{I}_k\delta q_k\text{\hspace{1em}(5)}$$
结合式$(4)$与$(5)$，可得：
$$\delta W(I)=\sum _{k=1}^N{I}_k\cdot \delta {\mathbf{r}}_k=\sum _{k=1}^N{I}_k\delta q_k\text{\hspace{1em}(3 - 18)}$$

利用广义虚位移的任意性，最终推得：
$$I_k=\sum _{i=1}^N{\mathbf{I}}_i\cdot \frac{\partial {\mathbf{r}}_i}{\partial q_k}=\sum _{i=1}^N\left(I_i\frac{\partial x_i}{\partial q_k}+I_i\frac{\partial y_i}{\partial q_k}+I_i\frac{\partial z_i}{\partial q_k}\right)$$
该式形式上与广义力的计算式一致，体现了广义冲量与广义坐标、虚位移等的关联 。

题目

两物体的质量分别为$m_1$和$m_2$，恢复因数为$e$，产生对心正碰撞.碰撞前两物体质心速度分别为$v_{11}$、$v_{21}$，碰撞后为$v_{12}$、$v_{22}$。

解

两物体能碰撞的条件是$v_1>v_2$，取两物体为研究的质点系，因无外碰撞冲量，质点系动量守恒。

设碰撞结束时，两物体质心的速度分别为$v_1^{\prime }$和$v_2^{\prime }$，取$BB$直线为投影轴，由冲量定理，有
$$m_1{v}_1+m_2{v}_2=m_1{v}_1^{\prime }+m_2{v}_2^{\prime }\text{\hspace{1em}(a)}$$
由恢复因数定义，有
$$e=\frac{v_2^{\prime }-v_1^{\prime }}{v_1-v_2}\text{\hspace{1em}(b)}$$
联立式$(a)$和式((b)$二式，解得
$$\{\begin{array}{l}{v}_1^{\prime }=v_1-(1+e)\frac{m_2}{m_1+m_2}(v_1-v_2)\\ v_2^{\prime }=v_2+(1+e)\frac{m_1}{m_1+m_2}(v_1-v_2)\end{array}\text{\hspace{1em}(c)}$$
在理想情况下，$e=1$，有
$$\{\begin{array}{l}{v}_1^{\prime }=v_1-\frac{2m_2}{m_1+m_2}(v_1-v_2)\\ v_2^{\prime }=v_2+\frac{2m_1}{m_1+m_2}(v_1-v_2)\end{array}$$
如果$m_1=m_2$，则$v_1^{\prime }=v_2$，$v_2^{\prime }=v_1$，即两物体在碰撞结束时交换了速度。
当两物体做塑性碰撞时，即$e=0$，有 $$v_1^{\prime }=v_2^{\prime }=\frac{m_1{v}_1+m_2{v}_2}{m_1+m_2}$$
即碰撞结束时，两物体速度相同，一起运动。
以$T_1$和$T_2$分别表示此两物体组成的质点系在碰撞过程开始和结束时的动能，则有 $$T_1=\frac{1}{2}{m}_1{v}_1^2+\frac{1}{2}{m}_2{v}_2^2,T_2=\frac{1}{2}{m}_1{v}_1^{\prime 2}+\frac{1}{2}{m}_2{v}_2^{\prime 2}$$

在碰撞过程中质点系损失的动能为 $$\begin{array}{rl}\Delta T& =T_1-T_2\\ & =\frac{1}{2}{m}_1(v_1^2-v_1^{\prime 2})+\frac{1}{2}{m}_2(v_2^2-v_2^{\prime 2})\\ & =\frac{1}{2}{m}_1(v_1-v_1^{\prime })(v_1+v_1^{\prime })+\frac{1}{2}{m}_2(v_2-v_2^{\prime })(v_2+v_2^{\prime })\end{array}$$
将式$(c)$代入上式，再结合式$(b)$ $v_2^{\prime }-v_1^{\prime }=e(v_1-v_2)$推导（过程略），可得两物体在正碰撞过程中损失的动能 $$\Delta T=T_1-T_2=\frac{m_1{m}_2}{2(m_1+m_2)}(1-e^2)(v_1-v_2{)}^2\text{\hspace{1em}(d)}$$

理想弹性碰撞（$e=1$）：
由$(d)$得$\Delta T=0$，即动能无损失，碰撞前后系统动能守恒。

• 塑性碰撞（$e=0$）：
  代入$(d)$得：
  $$\Delta T=T_1-T_2=\frac{m_1{m}_2}{2(m_1+m_2)}(v_1-v_2{)}^2$$
  若碰撞前$v_2=0$（第二物体静止），则：
  $$\Delta T=\frac{m_1{m}_2}{2(m_1+m_2)}{v}_1^2$$ 结合$T_1=\frac{1}{2}{m}_1{v}_1^2$，可改写为： $$\Delta T=\frac{m_2}{m_1+m_2}{T}_1=\frac{1}{\frac{m_1}{m_2}+1}{T}_1\text{\hspace{1em}(e)}$$

• 当$m_2\gg m_1$时，$\Delta T\approx T_1$，即质点系在碰撞开始时的动能几乎完全损失于碰撞过程中。这种情况对于锻压金属最理想，锻压时希望金属变形消耗能量，砧座（$m_2$大）动能变化小 。

• 当$m_2\ll m_1$时，$\Delta T\approx 0$，适合打桩场景。打桩时希望锤（$m_1$大）保留动能驱动桩（$m_2$小）前进，减少能量浪费 。

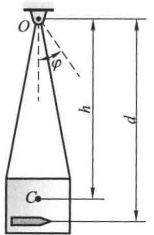
如图所示为一测量子弹速度的装置，称为射击摆，其是一个悬挂于水平轴$O$ 的填满砂土的筒。当子弹水平射入砂筒后，使筒绕轴 $O$ 转过一偏角$\phi$，测量偏角的大小即可求出子弹的速度。已知摆的质量为 $m_1$，对于轴 $O$ 的转动惯量为$J_O$，摆的重心$C$ 到轴$O$的距离为$h$。子弹的质量为 $m_2$，子弹射入砂筒时子弹到轴 $O$的距离为$d $。悬挂索的重量不计，求子弹的速度。

解

以子弹与摆组成的质点系为研究对象，子弹射入砂筒直到与砂筒一起运动可近似为碰撞过程。外碰撞冲量对轴 $O$ 的矩等于零，因此碰撞开始时质点系的动量矩 $L_{O1}$ 等于碰撞结束时的动量矩 $L_{O2}$。 设碰撞开始时子弹速度为 $v$，则
$$L_{O1}=m_{2}dv$$
设碰撞结束时摆的角速度为 $\omega$，则
$$L_{O2}=J_O\omega +m_2{d}^2\omega =(J_O+m_2{d}^2)\omega$$
因 $L_{O1}=L_{O2}$，解得
$$v=\frac{J_O+m_2{d}^2}{m_{2}d}\omega$$
碰撞结束后，摆与子弹一起绕轴 $O$ 转过角度 $\phi$，应用动能定理，有
$$0-\left(\frac{1}{2}{J}_O{\omega }^2+\frac{1}{2}{m}_2{d}^2{\omega }^2\right)=-m_{1}g(h-h\cos \phi )-m_{2}g(d-d\cos \phi )$$
即
$$\frac{1}{2}(J_O+m_2{d}^2){\omega }^2=(m_{1}h+m_{2}d)(1-\cos \phi )g$$
因 $1-\cos \phi =2{\sin }^2\frac{\phi }{2}$，代入上式中，解得
$$\omega =\sqrt{\frac{m_{1}h+m_{2}d}{J_O+m_2{d}^2}g}\cdot 2\sin \frac{\phi }{2}$$
于是得子弹射入砂筒前的速度为
$$v=\frac{2\sin \frac{\phi }{2}}{m_{2}d}\sqrt{(J_O+m_2{d}^2)(m_{1}h+m_{2}d)g}$$