计算机算术5-整形除法
1.1 基础知识
- 英文简写
以Z/D = (Q, R)为例
Z = numerator (dividend),分子,被除数
D = denominator (divisor),分母,除数
Q = quotient,商
R = Remainder,余数 - 基础算法
s(j+1)=s(j)−q(k−j)dr(k−j) s^{(j+1)} = s^{(j)} - q_{(k-j)}dr^{(k-j)} s(j+1)=s(j)−q(k−j)dr(k−j)
其中s(0)=zs^{(0)} = zs(0)=z; k 表示商的位数,sjs^jsj表示部分余数,为了让后续推导顺利进行,这里给sjs^jsj乘上一个rjr^jrj, 上式变为:
s(j+1)=rs(j)−qk−jdrks^{(j+1)} = rs^{(j)} - q_{k-j}dr^k s(j+1)=rs(j)−qk−jdrk - robertson图
下一次余数和当前余数的关系图, 也即s(j+1)和rs(j)s^{(j+1)} 和rs^{(j)}s(j+1)和rs(j)的关系图, 核心目的是用来选商的。
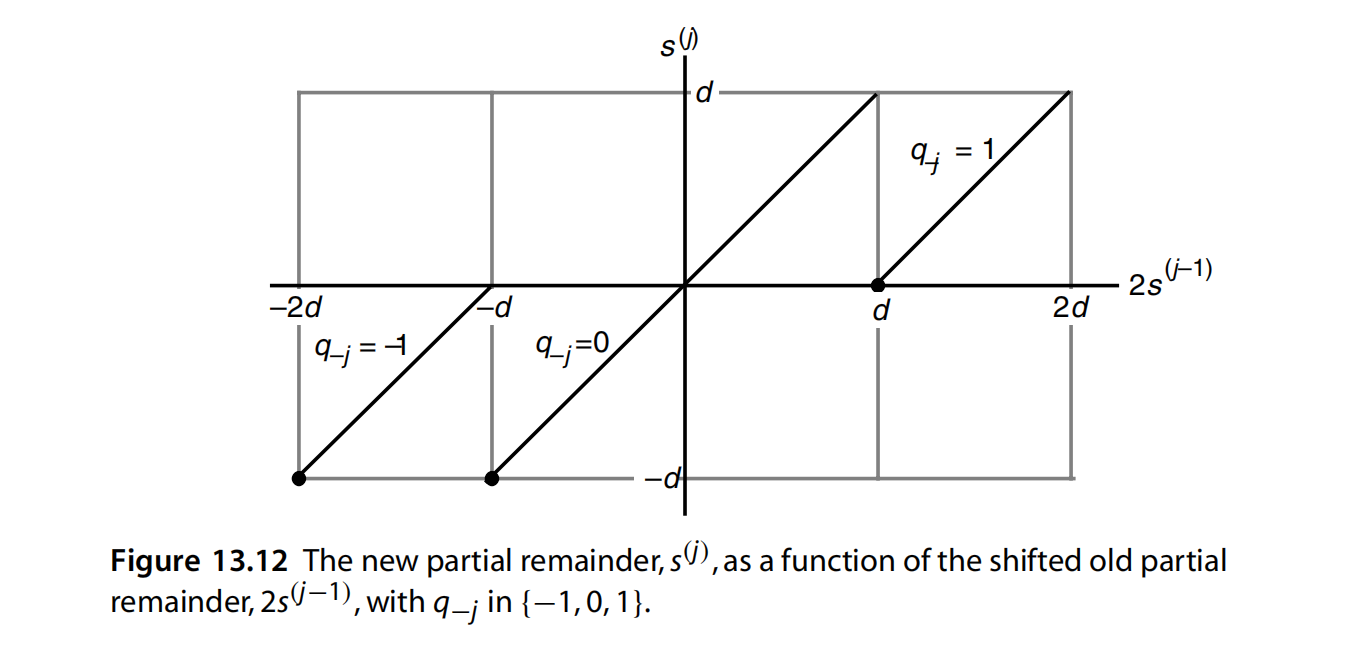
但如上图所示,这样比较大小进行选商太复杂了,如果边界是个常数就好了
1.2 基本分类
- 恢复余数除法(Restoring Remainder)、不恢复余数除法(Non-redstoring Remaind)、SRT除法(SRT Division)等算法。
- 牛顿迭代法、Goldschmidt算法等算法。
上面两类的区别是,第一类每次迭代都可确定1位的商,并且是基于加法的,即通过加法操作迭代来收敛结果,称作加性归一化的(additive normalization)。
第二类的收敛速度是平方级的,例如可能第i次能收敛n bit的商,第i+1次就能收敛2n bit的商了,这类算法是基于乘法操作的,即通过乘法操作来收敛结果,称作乘性归一化的(multiplicative normalization)。
2. 基本算法
2.1 恢复余数除法-慢速除法
慢速算法通过循环等式,对余数R进行迭代:
Rj+1=B∗Rj−qn−(j+1)∗D R_{j+1} = B * R_j - q_{n-(j+1)}*D Rj+1=B∗Rj−qn−(j+1)∗D
其中RjR_jRj是第j个部分余数, B是基;qn−(j+1)q_{n-(j+1)}qn−(j+1)是商的第n-(j+1)位,例如第一次迭代(j=0)产生qn−1q_{n-1}qn−1,商的最高位。n是商的位数,D是除数.
其中R=RnR_nRn, N = R0R_0R0, 将上面递归计算式带入得到
Rn=2nN−QDR_n = 2^nN-QDRn=2nN−QD
恢复余数除法的操作是先更新余数,如果余数小于0,则表明更新余数上的商是错误的,所以我们选择正确的商,并将余数恢复到正数(R+D)

2.2 不恢复余数除法
不恢复余数除法使用数集{-1, 1}, 在这种算法下,每位数字的基是{-1,1}, 而非{0, 1}, 例如-3 = 4’b-111-1.
不恢复余数法的操作是先判断余数大小,如果余数大于0,更新R=2*R-D;如果余数小于0;更新R=2R+D
R := N
D := D << n -- R and D need twice the word width of N and Q
for i = n − 1 .. 0 do -- for example 31..0 for 32 bitsif R >= 0 thenq(i) := +1R := 2 * R − Delseq(i) := −1R := 2 * R + Dend if
end
-- Note: N=numerator, D=denominator, n=#bits, R=partial remainder, q(i)=bit #i of quotient.
由于这种方法得到的结果是非标准形式,因此需要对商在最后一步进行转化。转化方式如下:
例如: Q = 111(-1)1(-1)1(-1)
则P = 11101010, N=00010101
Q = P-M = 11010101
最后还需要判断一次余数的正负,如果最后一次余数为负,则Q= Q-1
if R < 0 thenQ := Q − 1R := R + D -- Needed only if the remainder is of interest.
end if
3. 小结
- 除法分为恢复余数除法和不恢复余数除法,两者的基都是非冗余基,其中不恢复余数除法的基可以为负数,因此需要对商进行转换
- 在进行除法运算时,我们会先将除数(d)进行左移,使得除数和被除数进行对齐,最后将余数进行右移。
参考链接:
https://www.cnblogs.com/devindd/articles/17633558.html
