c++ --- priority_queue的使用以及简单实现

前言

priority_queue是C++容器之一，意为优先级队列，虽说叫做队列，但是其底层结构是堆，唯一和队列有关是使用此容器时包含的标准头文件是queue，通过此容器的学习，会学习到一个新的知识，仿函数。

一、priority_queue的使用

priority_queue的接口和stack与queue的基本一样，主要是push，pop，top，empty，size这些接口，只是底层的结构不同。

需要注意的是底层默认创建大堆结构，需要变成创建小堆结构，这里需要使用新的知识，仿函数，仿函数的详细介绍留在简单实现板块；还有同样因为数据有特殊的顺序，所以底层不支持迭代器遍历。

// 在这里仿函数是第三个模板参数，控制的是创建堆的结构
// greater --- 更大的
// less --- 更小的
// 不过标准库里的是less控制大堆，greater控制小堆，是反过来的，这一点需要注意一下
// 标准库提供的接口和前面的stack，queue相似，主要就是push，pop，top，size，empty这几个
// 使用起来也是差不多的，同样因为数据有特殊的顺序，所以底层不支持迭代器遍历
// 尽管堆的底层是数组，但是底层没有实[]的重载。// 创建一个堆的对象
//priority_queue<int> hp;
priority_queue<int, vector<int>, greater<int>> hp;hp.push(4);
hp.push(2);
hp.push(6);
hp.push(7);
hp.push(1);
hp.push(8);// 循环取堆顶元素打印
while (!hp.empty())
{cout << hp.top() << " ";hp.pop();
}
cout << endl;

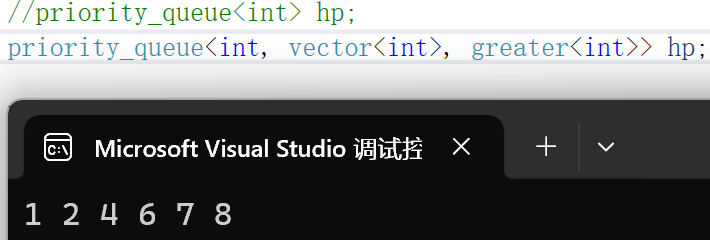
打印结果：
此时仿函数是greater，创建的是小堆，循环取堆顶元素则是升序排列。

二、priority_queue的简单实现

1.整体结构

priority_queue的底层是一个堆结构，并且堆结构是由数组实现的完全二叉树，所以这里直接使用容器适配器，默认适配vector，来作为priority_queue的结构。

template<class T, class Container = vector<T>>
class priority_queue
{
public://………………// 各种方法
private:Container _con;
};

2.主要方法

priority_queue的主要接口就是push，pop，top，empty，size。

push

由于堆结构本身就有性质，要么是大堆，要么就是小堆，所以这里在堆尾插入完数据后需要调整数据的位置，以满足堆的结构。

// 在堆尾入数据
void push(const T& x)
{// 插入数据_con.push_back(x);// 向上调整算法Adjust_up(size() - 1);}// 向上调整算法
void Adjust_up(size_t child)
{// 已知孩子节点求双亲节点size_t parent = (child - 1) / 2;// 最坏的情况child调整至根节点才结束while (child > 0){// 大堆，谁大谁向上调整// 小堆，谁小谁向上调整if (_con[child] < _con[parent]){swap(_con[child], _con[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}

在向上调整算法中，参数接收的是孩子节点的下标，根据二叉树的性质可知双亲节点的下标 = （孩子节点 - 1）/ 2，求出双亲节点的下标后比较它们两个的大小，孩子节点大（大堆）/ 小（小堆）于双亲节点，则进行交换，随后更新child和parent的位置，指向下一棵子树，若插入后满足所需要的堆结构，则直接跳出循环，最坏的情况下child调整至根节点才结束，所以这里的循环结束条件是child <= 0。

pop

由于堆底层是数组，并且堆的pop操作是在堆顶进行的，所以相当于进行头删操作，这样效率较低，首先先将堆顶数据和堆尾数据进行交换，这样一来需要删除的数据就在堆尾，而数组删除最后一个数据效率很高，直接将其删除掉即可，然后调整堆结构即可，这里使用向下调整算法。

// 在堆顶出数据
void pop()
{// 删除堆顶元素，先将堆顶和堆尾元素交换，再删除swap(_con[0], _con[_con.size() - 1]);_con.pop_back();// 向下调整算法Adjust_down(0);
}// 向下调整算法
void Adjust_down(size_t parent)
{// 已知双亲节点求左孩子节点，右孩子节点即左孩子 + 1size_t child = parent * 2 + 1;// 最坏的情况是根节点调整到叶子节点while (child < size()){// 首先右孩子得存在合法// 如果右孩子大于/小于左孩子，则child走到大/小的一方if (child+1 < size() && _con[child + 1] < _con[child]){++child;}// 大堆，谁大谁向上调整// 小堆，谁小谁向上调整if (_con[child] < _con[parent]){swap(_con[child], _con[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}

在向下调整算法中，参数接收的是根节点的下标，根据二叉树的性质可知左孩子节点 = 双亲节点 * 2 + 1，右孩子则是左孩子 + 1；在此算法中额外多出一步是比较左右孩子的大小关系，当堆结构为大堆时，child走到大的那一个孩子处，同理当堆结构为小堆时，child走到小的那一个孩子处（这一步要注意右孩子的下标需要存在合法），之后就和向上调整算法里的一样，孩子节点和双亲结点比较，谁大 / 小 就进行交换，随后更新child和parent的位置，走到下一棵子树的位置继续进行调整，若满足所需要的堆结构，则直接跳出循环，最坏的情况是根节点调整到叶子节点才结束，所以这里的循环结束条件是child >= 堆的szie。

top

此接口和下面的两个接口都直接使用适配即可。

// 取堆顶元素
const T& top() const
{return _con[0];
}

empty

// 判空
bool empty()
{return _con.empty();
}

size

// 取有效元素个数
size_t size() 
{return _con.size();
}

三、构造

迭代器区间构造

priority_queue支持迭代器区间构造，并且底层实现的是函数模板形式，所以我们也去实现函数模板形式。

// 迭代器区间构造
template<class InputIterator>
priority_queue(InputIterator first, InputIterator last)// 先将此迭代器区间入堆 --- _con是容器，支持直接迭代器区间构造:_con(first,last)
{// 然后就是向下调整建堆 --- 因为此时还不是堆结构for (size_t i = (size() - 1 - 1) / 2; i > 0; i--){Adjust_down(i);}
}

这里初始化列表里直接复用适配器的迭代器区间构造即可，然后虽入了数据，但是此时不是一个堆结构，同样需要进行调整，这里采用的是向下调整算法，至于为什么不使用向上调整算法，因为向上调整算法的时间复杂度高于向下调整算法，时间复杂度详情请回顾我的数据结构 — 堆 的这篇博客（link）

在向下调整建堆中，由于是向下调整，双亲节点和孩子节点进行比较向下调整，所以这里的for循环的循环变量 i 也就是双亲节点的下标，并且二叉树的最后一层节点是叶子节点，所以双亲节点的最后一层是倒数第二层，size() - 1 是最后一个位置的下标（不能保证此位置上有节点，此位置是右孩子），再减一就是左孩子的下标，已知孩子求双亲就是：(size() - 1 - 1) / 2，直至调整至根节点，所以循环结束条件就是i <= 0。

默认构造

由于我们自己写了一种构造，编译器就不再生成默认构造了，而默认构造能满足我们的需求，所以这里强制让编译器生成默认构造。

// 由于我们自己写了一种构造，编译器就不生成默认构造了
// 所以这里强制让编译器生成
priority_queue() = default;

四、仿函数

所谓仿函数，也叫做函数对象，它其实是一个类，其中重载了运算符operator()，使得这个类能够像函数一样被调用。
回到堆的代码中，在向上或者向下调整算法里面，我们控制大堆小堆结构是通过孩子和双亲大小关系来确定的，但是这个关系是固定死的，要么大于，要么小于，这里就可以使用仿函数，不用写死关系，通过调用仿函数创建的对象去调用运算符()，在此重载内部再去确定比较关系即可。

// 这个就是仿函数 / 函数对象
// 仿函数代替的就是C语言的函数指针
// 简单来说就是一个类，通过这个类类型创建的对象去模拟函数那样被调用
template<class T>
struct less
{bool operator()(const T& x, const T& y){return x < y;}
};template<class T>
struct greater
{bool operator()(const T& x, const T& y){return x > y;}
};// 使用仿函数控制大小比较关系
// 需要多增加一个模板参数
template<class T, class Container = vector<T>,class Compare = less<T>>
class priority_queue

回到向上调整算法中，在方法内部通过Compare创建了一个对象com，在孩子和双亲比较的逻辑里替换了之前的固定写死一方的大小关系，变成通过com对象去调用运算符()，这样就看起来像是调用了函数，这就是仿函数。

// 向上调整算法
void Adjust_up(size_t child)
{Compare com;size_t parent = (child - 1) / 2;while (child > 0){//if (_con[child] < _con[parent])if (com(_con[parent], _con[child])){swap(_con[parent], _con[child]);child = parent;parent = (child - 1) / 2;}else{break;}}
}

调用关系如下图所示：
这里的参数x接收的就是parent，参数y接收的就是child。

同理向下调整算法里parent和child的比较逻辑，child和child+1的比较逻辑也是如此替换。
需要注意的是对于类模板而言使用仿函数时这里传递的是类型，而对函数模板而言使用仿函数时传递的则是对象。