机器学习——决策树(DecisionTree)
决策树(Decision Tree)详解:原理、构建、剪枝与实践
在机器学习算法中,决策树(Decision Tree) 是一种经典、直观且易于解释的监督学习方法。它模拟人类的思维过程,通过“是/否”问题逐步将数据划分,最终形成一棵可以用于分类或回归的“树”。
本文将系统介绍决策树的核心原理、构建流程、剪枝技巧、优缺点以及代码实践。
一、什么是决策树?
决策树是一种树形结构模型,每个内部节点表示对一个特征的判断,每个分支代表判断结果,每个叶子节点表示一个类别或预测值。
用于分类任务:称为分类树(Classification Tree)
用于回归任务:称为回归树(Regression Tree)
二、决策树的核心思想
构建决策树的核心是:选择最佳特征将样本空间划分得最“纯净”。常见的划分标准有:
| 划分准则 | 用途 | 描述 |
|---|---|---|
| 信息增益(ID3) | 分类 | 衡量划分后信息的不确定性减少了多少 |
| 信息增益比(C4.5) | 分类 | 解决ID3偏好多值特征的问题 |
| 基尼指数(Gini Index,CART) | 分类 | 衡量节点的不纯度 |
| 均方差(MSE) | 回归 | 衡量预测值与真实值之间的误差 |
三、决策树的构建过程
以分类树为例,整体流程如下:
选择最优划分特征:根据信息增益、基尼指数等指标
节点划分数据集
对每个子集递归调用决策树构建算法
设置停止条件:
达到最大深度
节点样本数量小于阈值
所有样本标签相同
四、剪枝(Pruning):防止过拟合
决策树容易过拟合训练集,为了提高泛化能力,需要剪枝:
✅ 预剪枝(Pre-pruning)
在构建过程中提前停止划分,例如:
最大深度限制(
max_depth)最小样本分裂数(
min_samples_split)最小叶子节点样本数(
min_samples_leaf)
🔁 后剪枝(Post-pruning)
先生成整棵树,再自底向上剪去一些子树。例如:
使用验证集判断剪枝效果
成本复杂度剪枝(Cost Complexity Pruning)
五、决策树的优缺点
✅ 优点
简单直观,容易理解
不需要特征标准化
可处理离散和连续特征
对缺失值不敏感
可用于分类与回归
❌ 缺点
容易过拟合
对小样本数据不稳定
对类别不平衡敏感
可解释性好但精度可能不如集成方法(如随机森林、XGBoost)
六、决策树实战代码(分类)
| 品种 (三个品种共150条) | 花萼长度(cm) | 花萼宽度(cm) | 花瓣长度(cm) | 花瓣宽度(cm) |
|---|---|---|---|---|
| 山鸢尾(Iris-setosa)*50条 | 5.1 | 3.5 | 1.4 | 0.2 |
| 变色鸢尾(Iris-versicolor)*50条 | 7.0 | 3.2 | 4.7 | 1.4 |
| 维吉尼亚鸢尾(Iris-virginica)*50条 | 6.3 | 3.3 | 6.0 | 2.5 |
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import classification_report
from sklearn import tree
import matplotlib.pyplot as plt# 1. 加载数据(以鸢尾花为例)
from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data
y = iris.target# 2. 拆分训练集与测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)# 3. 创建并训练模型
clf = DecisionTreeClassifier(criterion='gini', max_depth=3, random_state=0)
clf.fit(X_train, y_train)# 4. 预测与评估
y_pred = clf.predict(X_test)
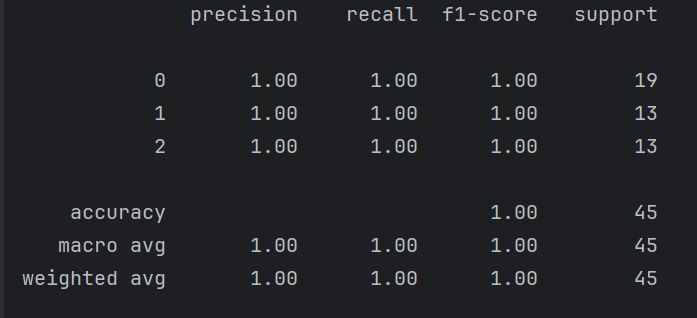
print(classification_report(y_test, y_pred))# 5. 可视化树结构
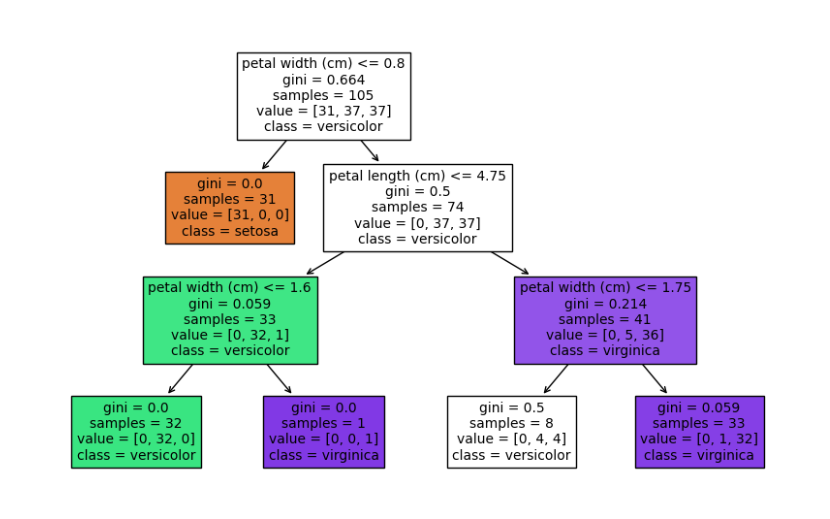
plt.figure(figsize=(10,6))
tree.plot_tree(clf, filled=True, feature_names=iris.feature_names, class_names=iris.target_names)
plt.show()
全是1.00,因为数据导致而已
七、超参数说明(分类器)
| 参数名 | 类型 | 默认值 | 说明 |
|---|---|---|---|
criterion | str | gini | 划分标准: • • |
splitter | str | best | 分裂策略: • • |
max_depth | int or None | None | 树的最大深度,限制深度可以防止过拟合 |
min_samples_split | int or float | 2 | 内部节点再划分所需的最小样本数(整数或比例) |
min_samples_leaf | int or float | 1 | 叶子节点所需的最小样本数(整数或比例) |
min_weight_fraction_leaf | float | 0.0 | 每个叶子节点所需的最小权重比例(对样本加权时有用) |
max_features | int, float, str, or None | None | 每次分裂考虑的最大特征数 • • • • |
max_leaf_nodes | int or None | None | 限制叶节点总数,控制模型复杂度 |
min_impurity_decrease | float | 0.0 | 节点划分的最小信息增益,低于则不分裂 |
| 参数名 | 类型 | 默认值 | 说明 |
|---|---|---|---|
random_state | int or None | None | 随机数种子,确保结果可复现 |
class_weight | dict, 'balanced', or None | None | 类别权重设置,常用于处理类别不平衡 • |
| 参数名 | 类型 | 默认值 | 说明 |
|---|---|---|---|
ccp_alpha | float | 0.0 | 成本复杂度剪枝参数(Cost Complexity Pruning) • 大于 0 时会自动剪枝,推荐配合交叉验证调参 |
八、应用场景
客户流失预测
信贷风险评估
疾病诊断
销售策略优化
决策支持系统
九、与其它模型的对比
| 模型 | 可解释性 | 性能 | 是否易过拟合 |
|---|---|---|---|
| 决策树 | ⭐⭐⭐⭐ | ⭐⭐ | 容易 |
| 随机森林 | ⭐⭐ | ⭐⭐⭐⭐ | 不易 |
| 支持向量机 | ⭐⭐ | ⭐⭐⭐⭐ | 适中 |
| 神经网络 | ⭐ | ⭐⭐⭐⭐⭐ | 可能 |
十、总结
决策树是一个适合入门的机器学习模型,其直观性和解释能力在很多实际场景中都有广泛应用。虽然它存在过拟合等问题,但通过剪枝或集成方法(如随机森林、XGBoost)可以有效改进。
📌 学会决策树,不仅能加深对机器学习本质的理解,也为进一步掌握集成学习打下了坚实基础!
