[ Leetcode ]---快乐数
题目链接
Leetcode快乐数
题目描述

如下图:
题目解析:
1.双指针法
算法核心思路
判断快乐数的关键挑战是如何检测是否进入无限循环。这里使用了快慢指针法(Floyd 循环检测算法),这是一种高效检测循环的技巧:
- 慢指针:每次计算一次数字的平方和(走一步)
- 快指针:每次计算两次数字的平方和(走两步)
- 如果是快乐数:最终都会收敛到 1,此时快慢指针会相遇在 1
- 如果不是快乐数:快慢指针会在某个非 1 的数字处相遇(检测到循环)

算法执行流程示例
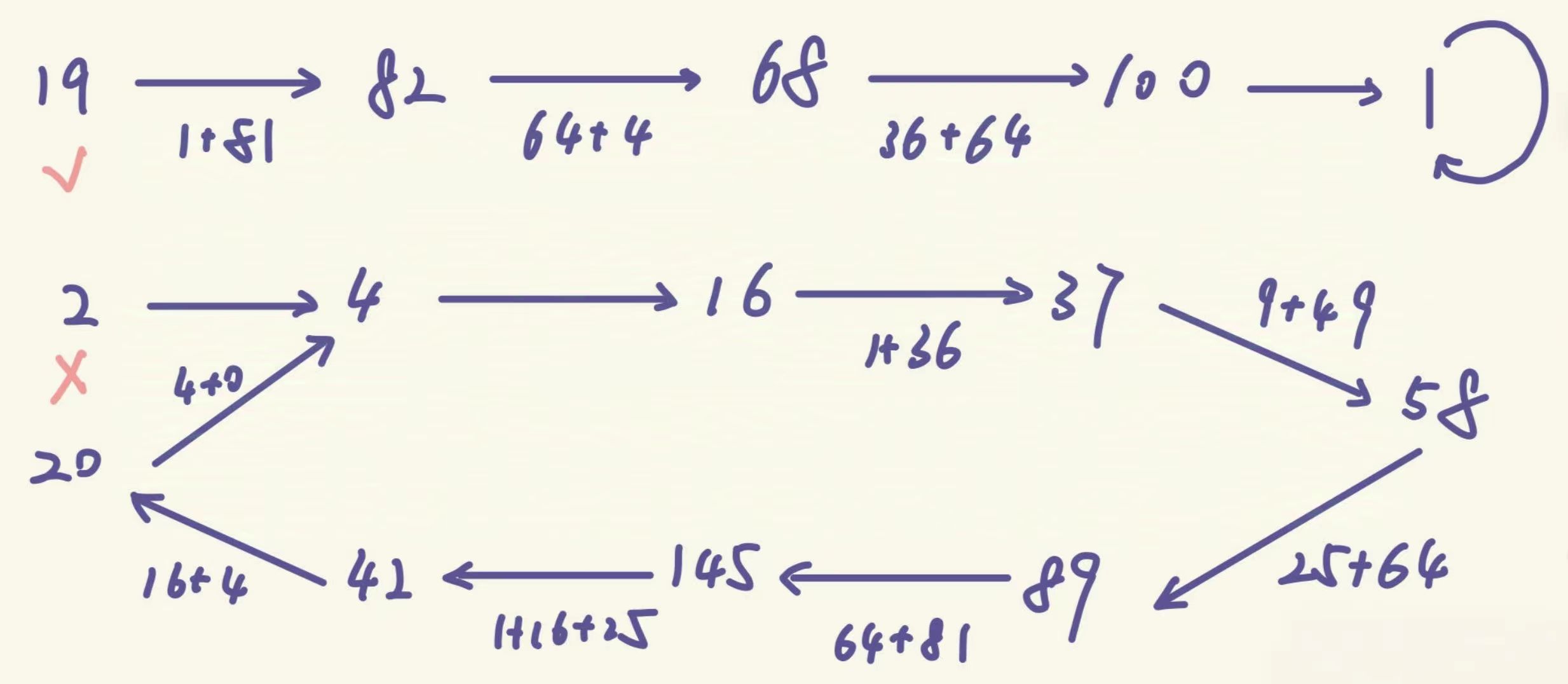
以非快乐数 11 为例,看看算法如何工作:
- 初始状态:slow=11,fast=11
- 第一次循环:
- slow = Sum(11) = 1² + 1² = 2
- fast = Sum(Sum(11)) = Sum(2) = 4
- 此时 slow≠fast,继续循环
- 第二次循环:
- slow = Sum(2) = 4
- fast = Sum(Sum(4)) = Sum(16) = 1² + 6² = 37
- 此时 slow≠fast,继续循环
- 后续循环中,快慢指针会逐渐接近,最终在某个非 1 的数字相遇,此时返回 false
算法复杂度分析
-
时间复杂度:O(log n)
- 每次计算平方和时,数字的位数大约是 log₁₀n
- 快慢指针相遇前最多执行 O (log n) 次操作
-
空间复杂度:O(1)
- 只使用了常数个额外变量,没有使用额外的数据结构
2.哈希表法
使用哈希表(Hash Set)求解快乐数问题是另一种直观且容易理解的方法。其核心思路是记录每次计算得到的平方和,如果某个平方和重复出现,说明进入了循环,该数不是快乐数;如果最终得到 1,则是快乐数。
哈希表解法思路
1.计算数字的各位平方和
2. 检查该平方和是否为 1:
若是 1,返回 true(是快乐数)
若不是 1,检查该平方和是否已在哈希表中:
- 若已存在,说明进入循环,返回 false(不是快乐数)
- 若不存在,将其加入哈希表,继续计算下一个平方和
完整代码:
代码解析
-
getSum 函数:与之前的 Sum 函数功能相同,计算一个数的各位数字平方和。
-
isHappy 函数:
- 使用
unordered_set<int> seen存储已经出现过的数字 - 循环计算平方和,直到结果为 1 或检测到循环:
- 若 n=1,返回 true(找到快乐数)
- 若 n 已在哈希表中,返回 false(检测到循环)
- 否则将 n 加入哈希表,继续计算下一个平方和
- 使用
执行流程示例(以 19 为例)
- 初始 n=19,哈希表为空
- 19 不在哈希表中,加入哈希表,计算下一个值:1²+9²=82
- 82 不在哈希表中,加入哈希表,计算下一个值:8²+2²=68
- 68 不在哈希表中,加入哈希表,计算下一个值:6²+8²=100
- 100 不在哈希表中,加入哈希表,计算下一个值:1²+0²+0²=1
- 此时 n=1,返回 true(19 是快乐数)
复杂度分析
-
时间复杂度:O(log n)
- 每次计算平方和处理 log₁₀n 位数字
- 最多处理 O (log n) 个不同的数字(因为平方和的增长有上限)
-
空间复杂度:O(log n)
- 最坏情况下,哈希表需要存储 O (log n) 个不同的数字
