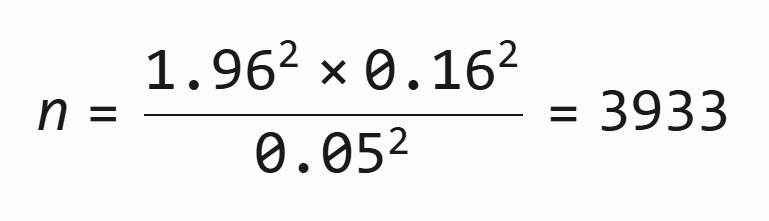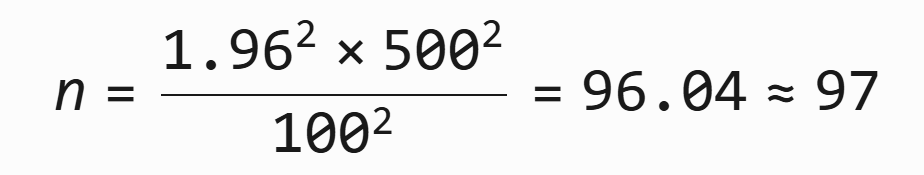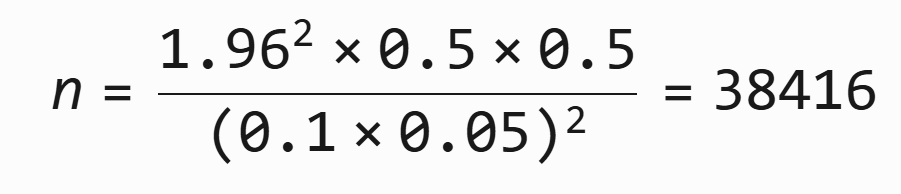第3章 AB实验的统计学知识
AB实验统计学相关知识
引言
AB实验是互联网产品优化的核心工具,通过随机抽样用户样本推断全体用户表现。然而,其科学性依赖于统计学原理,包括抽样分布、假设检验、功效分析等。本章将系统解析这些概念,结合费曼学习法——用简单案例阐释复杂理论——帮助读者轻松掌握核心知识。无论你是数据科学家、产品经理还是业务决策者,理解这些底层原理对正确设计、评估和解读AB实验至关重要。
一、随机抽样和抽样分布
1. 随机抽样的定义与意义
- 定义:从总体中按一定规则抽取部分个体组成样本的过程。简单随机抽样要求:
- 每个个体来自同一总体;
- 每次抽取独立且概率相同(无偏)。
- 意义:通过样本推断总体特征(如均值、标准差),避免全量检查的高成本。
- 例如:从500万日活用户中随机抽取100人,计算其使用时长的均值(样本均值)和标准差(样本标准差),作为总体参数的估计。
2. 点估计与抽样误差
- 点估计量:样本均值(
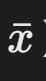 )和样本标准差(s)分别是总体均值(μ)和总体标准差(σ)的估计值。
)和样本标准差(s)分别是总体均值(μ)和总体标准差(σ)的估计值。 - 计算公式:
- 样本均值:
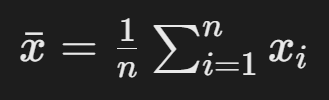
- 样本标准差:
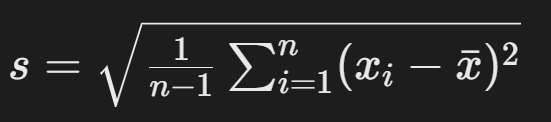
- 样本均值:
- 计算公式:
- 抽样误差:样本与总体的差异(
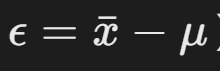 ),需量化其范围。
),需量化其范围。
3. 抽样分布与中心极限定理
- 抽样分布:反复抽样(如1000次)得到的样本均值的分布。
- 性质:
- 期望:
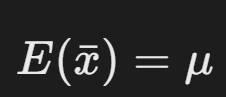 (无偏性);
(无偏性); - 标准差(标准误):
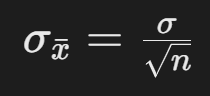 (样本容量越大,误差越小)。
(样本容量越大,误差越小)。
- 期望:
- 性质:
- 中心极限定理(CLT):无论总体分布形态如何,当样本容量n足够大(通常n≥30),样本均值的分布近似正态分布。例如:均匀分布在n=15时已接近正态(图3-2)。
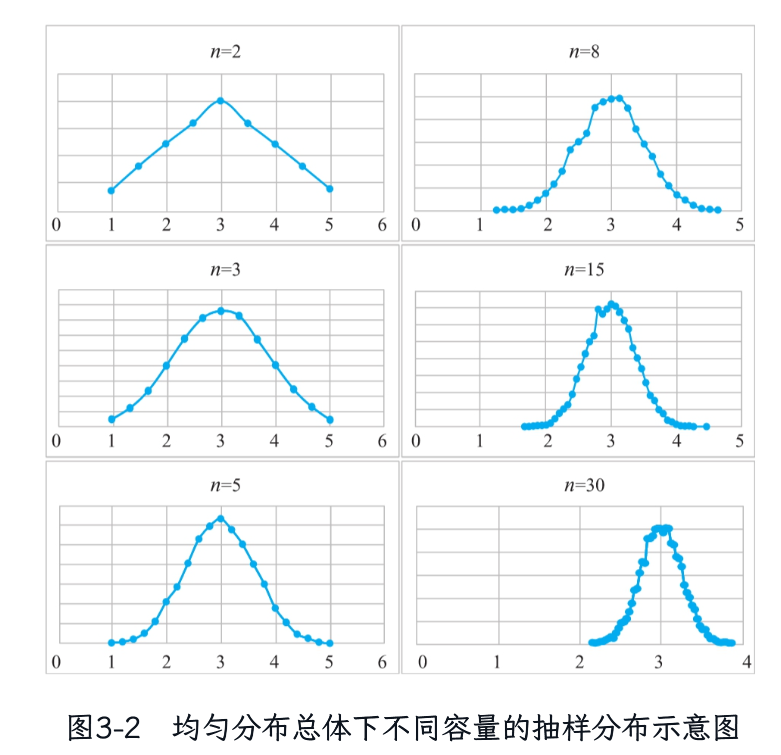
4. 样本容量与布形态
- 关键概念:
- 样本容量(n):单个样本中的个体数(如100人);
- 样本量:抽样次数(如1000次)。
- 影响:
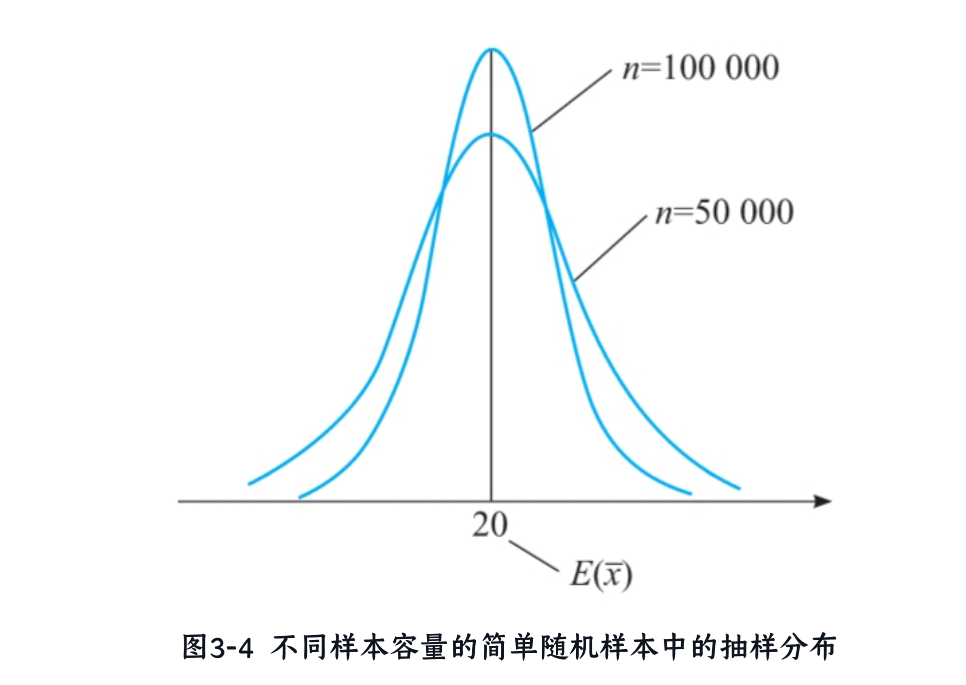
- n越大,标准误越小,抽样分布越集中(图3-4)。
- 极端情况:n=N(全量)时,xˉ=μ,无误差。
5. 概率计算与置信度
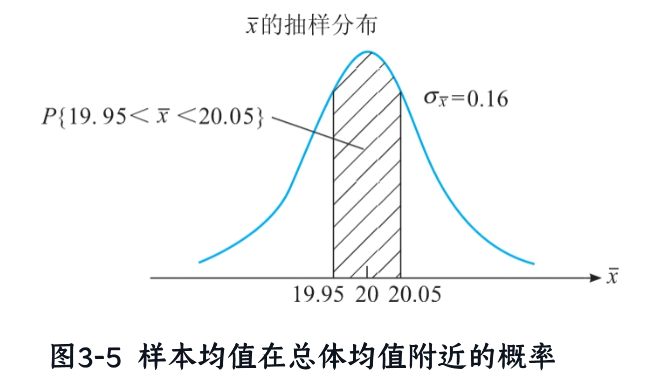
问题:计算样本均值落在μ±0.05分钟内的概率。
步骤:
- 已知μ=20,σxˉ=0.16(假设σ=1.6,n=100,根据
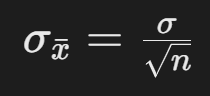 );
); - 计算标准化Z值:

- 查标准正态表得概率:P(19.95≤xˉ≤20.05)=0.6217−0.3783=0.2344。
结论:仅有23.44%的把握使误差在±0.05分钟内,需增大样本容量以提高置信度。
即:
6. 实际应用建议
- 增加样本容量:降低标准误,使分布更集中,提高估计精度。
- 分布选择:
- 总体正态 → 样本均值正态(任意n);
- 总体非正态 → n≥30时近似正态。
二、区间估计和置信区间
1. 基本概念
区间估计是通过样本统计量来估计总体参数的可能范围。与点估计(单一数值估计)不同,区间估计提供了一个范围,并附带一个置信水平(即该范围包含总体参数的概率)。
置信区间(Confidence Interval, CI)是区间估计的具体实现形式,表示在给定置信水平下,总体参数可能落入的范围。
2. 核心公式
对于总体均值μ的置信区间,公式为:
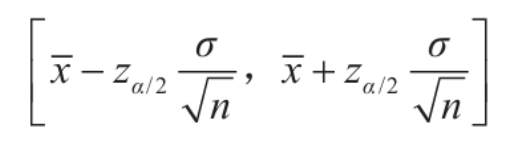
其中:
- xˉ:样本均值
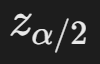 :标准正态分布的分位数(临界值)
:标准正态分布的分位数(临界值)- σ:总体标准差(若未知可用样本标准差s替代)
- n:样本量
- α:显著性水平(1 - 置信水平)
3. 关键组成部分
边际误差(Margin of Error)
公式中  部分,表示估计的允许误差范围。对应问题中的 ε,即 μ=xˉ±ε。
部分,表示估计的允许误差范围。对应问题中的 ε,即 μ=xˉ±ε。
置信水平
如95%置信水平表示:重复抽样时,95%的置信区间会包含真实总体均值μ。
(注意:不能说“μ有95%概率落在当前区间内”,因为μ是固定值,区间是随机的。)
![]() 的确定
的确定
通过标准正态分布表查找。例如:
- 95%置信水平 → α=0.05 → z0.025=1.96
- 90%置信水平 → z0.05=1.645
4. 举例说明
假设:
- 样本均值 xˉ=50
- 总体标准差 σ=10
- 样本量 n=100
- 置信水平95%(α=0.05)
计算:
- 边际误差 =
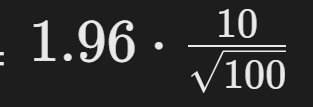 =1.96
=1.96 - 置信区间 =

结论:有95%的置信度认为总体均值μ在48.04到51.96之间。
5. 注意事项
- 正态性假设:当样本量足够大(如n≥30),中心极限定理保证样本均值近似正态分布;小样本时需用t分布。
- σ未知时:用样本标准差s替代σ,同时改用t分布临界值(tα/2)。
- 解释严谨性:置信水平是对方法(而非当前区间)的可靠性描述。
6. 常用置信水平
| 置信水平 | α | α/2 | zα/2 |
|---|---|---|---|
| 90% | 0.10 | 0.05 | 1.645 |
| 95% | 0.05 | 0.025 | 1.960 |
| 99% | 0.01 | 0.005 | 2.576 |
三、样本容量和边际误差
1. 基本概念
-
边际误差(Margin of Error, ε):表示估计值与真实值之间的最大允许偏差。例如,在用户使用时长的案例中,业务人员可以接受的平均使用时长误差不超过 0.05 分钟。
-
样本容量(n):指需要抽取的样本数量,以确保在给定的置信水平和边际误差下,估计值足够准确。
-
置信水平(1-α):表示估计结果的可信程度(如 95% 置信水平意味着,重复抽样时,95% 的置信区间会包含真实值)。
2. 均值类指标的样本容量计算
公式:
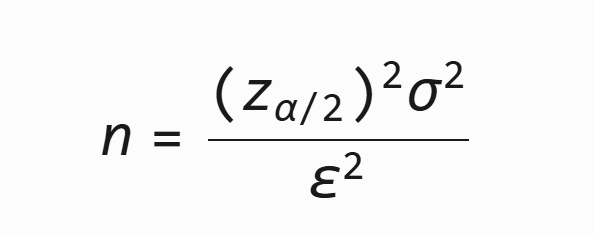
变量说明:
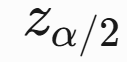 :标准正态分布的分位数(如 95% 置信水平下 z0.025=1.96)
:标准正态分布的分位数(如 95% 置信水平下 z0.025=1.96)- σ:总体标准差(若未知,可用样本标准差 s 代替)
- ε:允许的边际误差
示例 1(用户使用时长):
- 标准差 σ=0.16 分钟
- 允许误差 ε=0.05 分钟
- 计算:
即需要 3933 个样本 才能保证 95% 置信水平下误差 ≤ 0.05 分钟。
示例 2(员工工资):
- 标准差 σ=500 元
- 允许误差 ε=100 元
- 计算:
即需要 97 名员工 才能保证 95% 置信水平下误差 ≤ 100 元。
关键结论:
- 边际误差减半,样本容量需增至 4 倍(指数关系)。
- 例如,若 ε 从 100 元降至 50 元,则 n 从 97 增至 385。
3. 比率类指标的样本容量计算
公式:
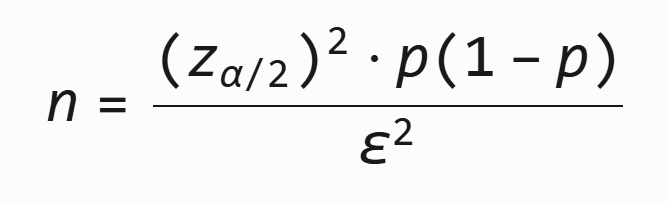
变量说明:
- p:比率(如点击率),若未知,可用经验值或保守估计 p=0.5(此时样本量最大)
- ε:允许的边际误差(如 5% 的点击率变化)
示例(点击率估计):
- 假设点击率 p=10%,允许误差为 5% 的 p(即 ε=0.1×0.05=0.005)
- 保守计算(取 p=0.5):
即需要 38,416 个用户 才能保证 95% 置信水平下点击率误差 ≤ 5%。
4. 如何选择样本容量?
- 确定置信水平(通常 95%)。
- 估计标准差 σ 或比率 p(若未知,可用历史数据或保守估计)。
- 设定可接受的边际误差 ε(业务需求决定)。
- 计算最小样本容量,权衡精度与成本。
5. 实际应用中的注意事项
- 边际误差越小,样本量需求急剧增加(如 ε 减半,n 变 4 倍)。
- 比率类指标中,若 p 未知,取 p=0.5 最保守(保证样本量足够)。
- 实验成本考量:样本量增加可能延长实验周期或增加商业风险(如 A/B 测试中的用户损失)。
总结
- 均值类指标:样本容量与 σ2 成正比,与 ε2 成反比。
- 比率类指标:样本容量取决于 p(1−p),保守估计取 p=0.5。
- 业务决策:需在统计精度(小 ε)与实验成本(大 n)之间权衡。
四、假设检验
1. 为什么需要假设检验?
在AB实验中,直接比较两组均值(如实验组A和对照组B的人均时长)可能得出误导性结论。例如:
- A组均值=20min,B组均值=19.95min,差异仅0.05min。
- 但通过计算95%置信区间:
- A组区间:[19.92, 20.08]
- B组区间:[19.87, 20.02]
- 两组区间重叠,说明在95%置信水平下,无法确定A组是否显著优于B组。
核心问题:抽样误差可能导致观察到的差异是随机波动而非真实效果——假设检验通过统计方法判断差异是否显著。
2. 假设检验的基本步骤
1、设立假设:
- 原假设(H₀):两组无差异(如tA = tB)。
- 备择假设(H₁):两组有差异(如tA ≠ tB)。
2、构造检验统计量:
- 例如计算Z值:
若z=3.539(案例中Δ=0.2),远大于临界值1.96(α=0.05)。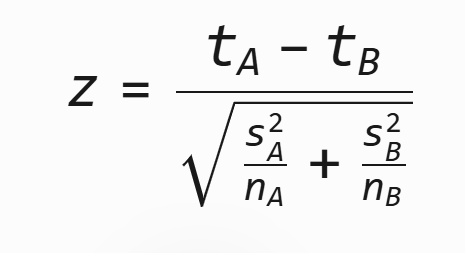
参考详细解释:【番外篇16】假设检验-CSDN博客
3、判断显著性:若P值(观测到极端值的概率)<显著性水平α(如0.05),拒绝H₀。
3. 两类错误与功效
在假设检验中,我们可能会犯两种错误:第一类错误(Type I Error) 和 第二类错误(Type II Error)。
第一类错误(假阳性,冤枉好人)
- 定义:当原假设 H0 为真(即没有真实效应)时,我们却错误地拒绝了 H0。
- 示例:小明没有作弊,但老师误判他作弊了。
- 统计学意义:这是“误报”错误,即错误地认为新策略有效,但实际上无效。
- 控制方法:通过显著性水平 α 控制,通常设定 α=0.05(即 5% 的犯错概率)。
第二类错误(假阴性,放过坏人)
- 定义:当备择假设 H1 为真(即存在真实效应)时,我们却未能拒绝 H0。
- 示例:小明确实作弊了,但老师没发现,认为他没作弊。
- 统计学意义:这是“漏报”错误,即错误地认为新策略无效,但实际上有效。
- 控制方法:通过 功效(Power) 控制,通常目标设定为 ≥80%。
| 错误类型 | 定义 | 控制方法 |
|---|---|---|
| 第一类错误 | H₀为真但被拒绝(假阳性) | 通过α控制(通常α=5%) |
| 第二类错误 | H₀为假但未被拒绝(假阴性) | 通过功效(1-β)控制(目标≥80%) |
功效(Power = 1 - β) 表示 当 H1 为真时,正确拒绝 H0 的概率。
参考:【番外篇17】统计功效(Power)-CSDN博客
- β 是第二类错误的概率(即 P(不拒绝 H0∣H1 为真))。
- 目标:通常希望功效 ≥ 80%,即至少有 80% 的概率能检测到真实效应。

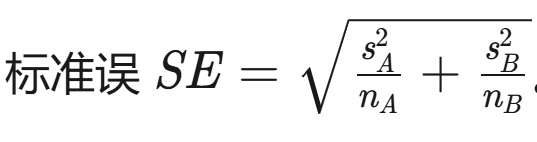
影响功效的因素:
- 样本量 n:样本越大,功效越高(更容易检测到小效应)。
- 效应量 Δ:效应越明显(如两组差异越大),功效越高。
- 方差 σ2:数据波动越小,功效越高。
- 显著性水平 α:α 越大(如 0.1 代替 0.05),功效越高(但第一类错误风险也增加)。
提升方法:
- 增加样本量 n(最直接的方法)。
- 减少方差 σ2(如优化实验设计,减少噪声)。
- 增大效应量 Δ(如优化策略,使效果更明显)。
- 调整 α 或 β(但需权衡第一类错误风险)。
4. 实际案例解析
案例1(人均时长实验):
- 观测Δ=0.2,计算z=3.539 > 1.96 → 拒绝H₀,认为新策略有效。
- 若Δ=0.1,z=1.77 < 1.96 → 无法拒绝H₀,需检查功效是否足够。
案例2(点击率实验):
- 若功效<80%,可能因样本不足导致无法检测真实差异,需延长实验或优化设计。
5. 常见误解与纠正
| 误解 | 正确解释 |
|---|---|
| "P值=0.05意味着H₀有5%为真" | P值是H₀成立时观测到极端数据的概率,非H₀本身概率。 |
| "不显著=无差异" | 可能因功效不足(样本量小或方差大)导致未能检测差异。 |
| "P值越小效果越强" | P值仅反映统计显著性,不代表实际效果大小(需结合效应量)。 |
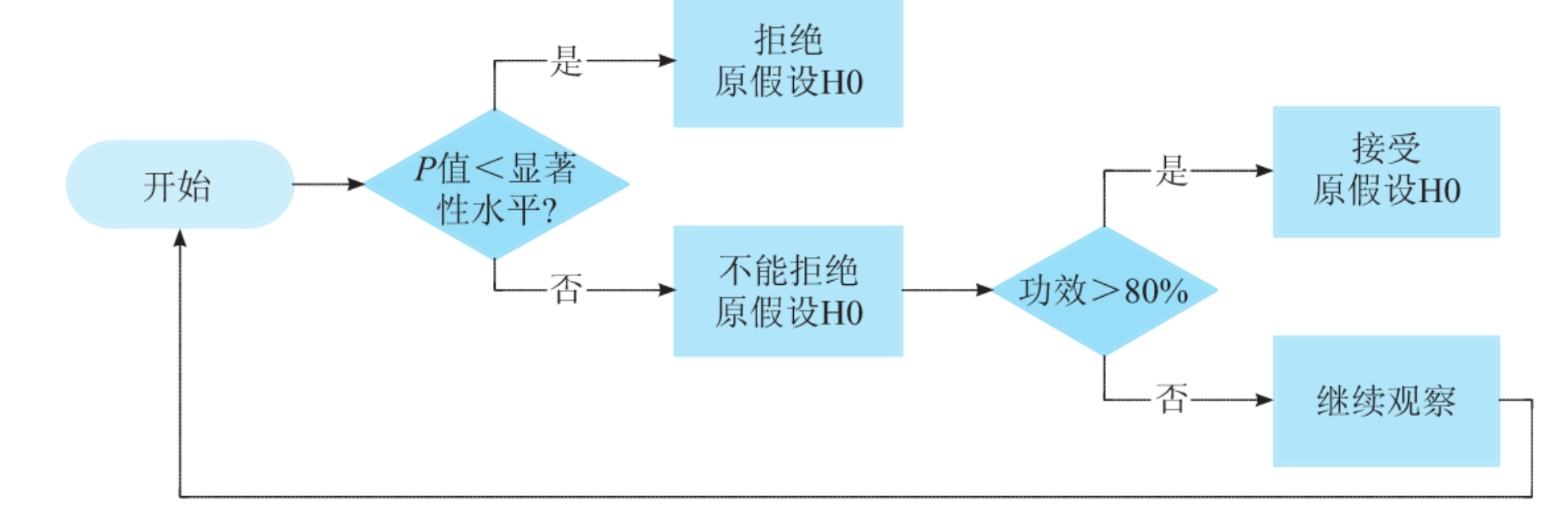
6. 决策流程图
根据P值与功效的判断逻辑:
- P值 < α → 拒绝H₀,认为策略有效。
- P值 ≥ α:
- 若功效≥80% → 倾向于接受H₀(策略可能无效)。
- 若功效<80% → 需继续实验或优化设计。
7. 总结
- 假设检验:通过统计方法区分随机波动与真实效果。
- 核心指标:P值(显著性)、功效(检验灵敏度)。
- 实践建议:
- 设定合理的α(如5%)和功效目标(如80%)。
- 避免仅依赖P值,需结合置信区间和效应量综合评估。
- P值告诉你“有没有发现差异”(显著性),功效告诉你“能不能发现差异”(灵敏度)
- P值显著说明这次可能不是运气,功效高说明实验本身靠谱,不容易漏掉真实效果。
- P值(显著性):好比“警报器响了没”,P<0.05 表示“这次检测到异常,可能真有不同”(但可能是误报)。
- 功效(灵敏度):好比“警报器灵敏度”,功效高(如80%)表示“只要真有异常,八成能响”,功效低则容易“该响不响”(漏报)。
- 如果P值显著(警报响了),且功效高(警报灵敏),结果更可信;
- 如果P值不显著,但功效低(警报不灵敏),可能是实验能力不足,而非真的没差异。
- P值 = 医生诊断“你有病”(P<0.05),但可能是误诊(假阳性)。
- 功效 = 这台检测仪“能查出80%的真病人”,如果功效低,查不出病可能是仪器太烂(而非你真健康)。
五、非参数检验
1. 核心概念
-
参数检验的局限
- 隐含前提:传统方法(t检验/z检验)要求数据满足独立同分布(i.i.d.),即样本独立且服从特定分布(如正态分布)。
- 现实挑战:实际场景常违背此前提。例如:
- 搜索场景:用户点击行为受历史记录影响(如看过优质条目后不再点击相似内容),导致条目间不独立。
- 数据分布复杂:可能非正态或形式未知。
-
非参数检验的核心思想
- 无需分布假设:不预设总体分布形式,完全依赖数据本身进行推断。
- 优势:
- 适用性广:无论正态分布与否均可使用。
- 规避理论计算:通过重采样模拟抽样分布,避免复杂数学推导。
- 灵活性:可处理复杂估计量(如中位数、分位数)。
2. 主流方法对比:Bootstrap vs. Jackknife
参考:【番外篇07】Delta、Jackknife、Bootstrap-CSDN博客
| 方法 | Bootstrap | Jackknife |
|---|---|---|
| 采样方式 | 有放回抽样(样本可重复) | 无放回删除(每次删除一个子集) |
| 样本构建 | 从原样本随机抽取容量为 n 的新样本 | 将样本分为 N 份,每次删除1份,用剩余 N−1 份构成新样本 |
| 计算效率 | 需大量重复抽样(如1000次) | 计算量更小(仅需 N 次删除操作) |
| 方差性质 | 精确估计 | 是Bootstrap方差的一阶近似 |
| 适用场景 | 小样本精度要求高 | 大规模数据(工程易实现) |
注:Jackknife的工程优化常将用户分桶聚合(如每桶包含 n 个用户),以桶为单位删除,显著降低计算量。
3. Bootstrap案例详解(中学生身高)
目标:用30个身高样本估计总体均值的95%置信区间。
步骤
- 重抽样:从原始样本中有放回地随机抽取 20个数据(如
[138.5, 138.5, 140.0, ..., 160.5]),允许重复。(解释一下30和20:30个原始样本数据(固定不变),每次从30个原始数据中抽20个可重复Bootstrap子样本) - 计算统计量:计算该次抽样的均值(如 μ=153.5)。
- 重复构建经验分布:重复上述过程 1000次,得到1000个均值估计值。
- 确定置信区间:
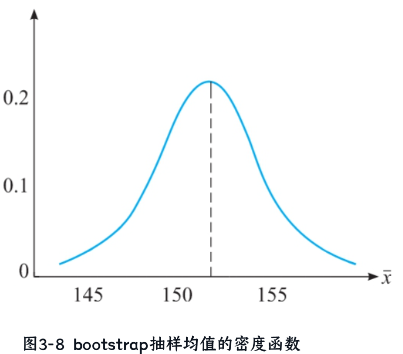
- 绘制1000个均值的密度函数图(图3-8),反映抽样分布。
- 通过最短区间长度法选择95%置信区间(如区间长度6.8),确保唯一性。
关键结论
- 样本容量影响:容量减小时(如从30→20),相同置信水平下置信区间变宽(估计精度下降)。
- 容量选择原则:需权衡计算成本与估计精度需求。
1000个Bootstrap均值的密度函数图
原始数据构成
- 输入:通过Bootstrap重采样生成的1000个均值(每个均值来自一次容量为20的子样本)。
- 例如:
[153.5, 152.8, 154.1, ..., 151.9](共1000个值)。- 密度函数图:通过核密度估计(Kernel Density Estimation, KDE)将离散的均值分布转化为连续概率密度曲线(如图3-8所示)。
- 横轴:均值取值范围(如150-160 cm)。
- 纵轴:概率密度(反映不同均值出现的相对可能性)。
图形特征
- 形状:
- 若原始数据接近正态分布 → 密度曲线对称且钟形;
- 若原始数据偏态 → 密度曲线左偏/右偏(如文档案例中身高数据可能右偏,因存在160.5 cm等高值)。
- 用途:直观展示Bootstrap统计量的变异性和置信区间边界。
最短区间长度法
在所有可能的95%置信区间中,选择 区间宽度最短 的一个,确保估计精度最高。
排序Bootstrap均值:将1000个均值按升序排列,得到有序序列:
[150.1, 150.3, ..., 155.6, 156.0]。滑动窗口搜索:
- 初始化一个覆盖95%数据的窗口(即包含1000×0.95=950个均值)。
- 从排序后的序列左端开始,滑动窗口逐步右移,计算每次窗口的区间长度:
- 第1窗口:
[150.1, 154.8]→ 长度=4.7- 第2窗口:
[150.3, 154.9]→ 长度=4.6- ...
- 第N窗口:
[151.0, 155.5]→ 长度=4.5(最短)。确定最优区间:选择所有窗口中长度最短的区间(如
[151.0, 155.5]),即为95%置信区间。
4. 非参数检验的核心价值
- 解决现实复杂性:适用于数据不独立、分布未知或非标准化的场景(如互联网行为数据)。
- 工程友好性:
- Jackknife通过分桶策略降低计算复杂度。
- Bootstrap通过模拟替代理论推导,适应复杂统计量。
- 推断鲁棒性:摆脱分布假设束缚,结论更普适。
5. 总结
非参数检验通过数据重采样(Bootstrap/Jackknife)构建经验分布,替代传统参数检验的理论分布假设。其优势在于无需独立同分布前提,尤其适用于现实场景中复杂、非标准化的数据推断。两种方法中,Jackknife因计算效率更高,更常用于大规模数据场景(配合分桶策略),而Bootstrap在小样本下提供更精确的估计。
六、方差估计问题
案例1:绝对差与相对差的方差估计
场景:比较两组用户的平均使用时长(单位:分钟)。
- 实验组(Yₜ):[10, 12, 11, 13, 14]
- 对照组(Y꜀):[8, 9, 10, 11, 12]
步骤1:计算均值
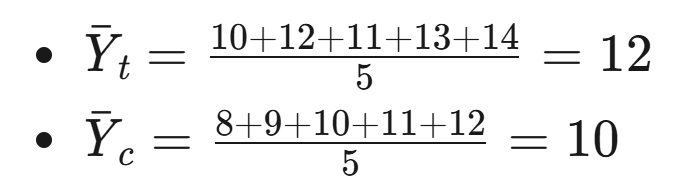
步骤2:计算绝对差(Δ)及其方差
- 绝对差:
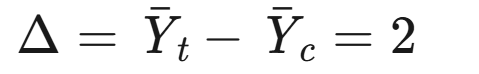
- 方差:
其中样本方差: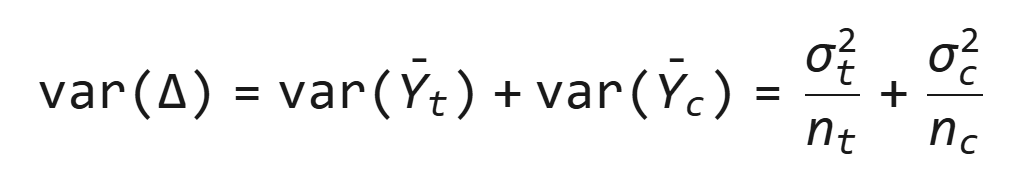
因此: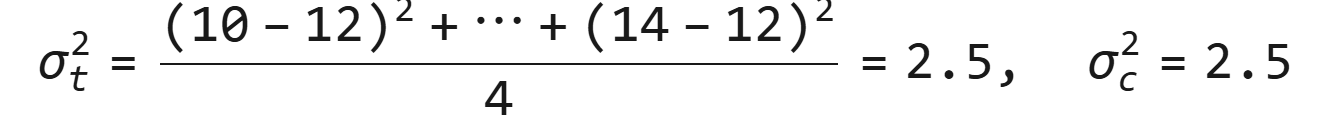
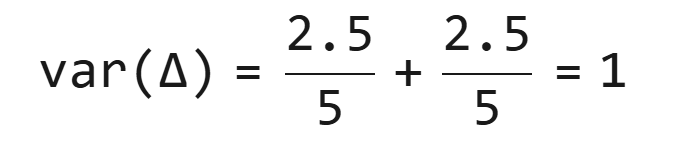
步骤3:计算相对差(Δ%)及其方差
- 相对差:
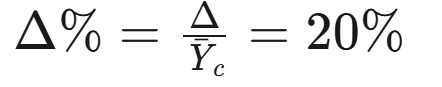
- 使用Delta方法近似:
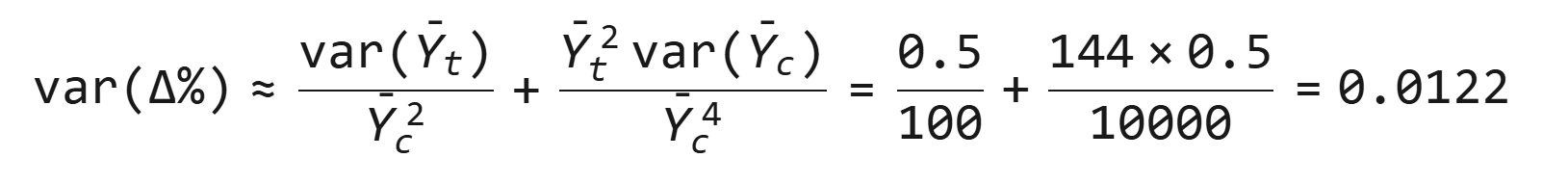
案例2:比率类指标(点击率CTR)的方差估计
场景:用户级随机化,但指标为页面级(点击量/浏览量)。
- 实验组:总点击量 Xt=50,总浏览量 Yt=1000
- 对照组:总点击量 Xc=40,总浏览量 Yc=800
步骤1:计算比率(CTR)
![]()
步骤2:用户级拆分(假设5个用户)
- 实验组用户贡献:[ (10,200), (12,250), (8,150), (15,300), (5,100) ]
- 对照组用户贡献:[ (8,160), (10,200), (6,120), (12,240), (4,80) ]
步骤3:计算用户级均值和协方差
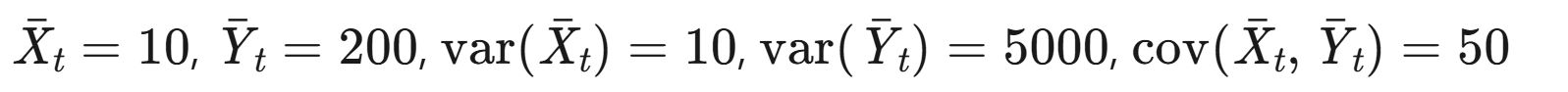
代入Delta方法:
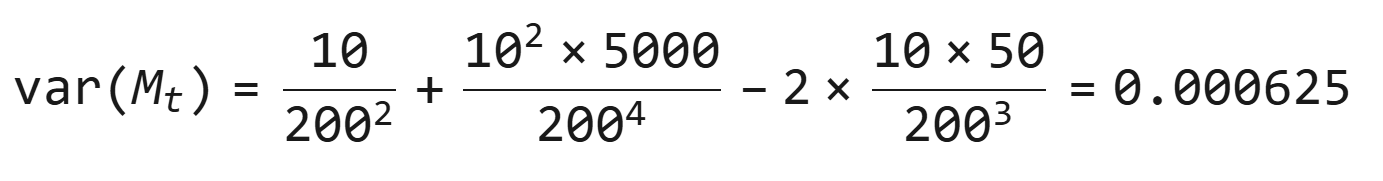
案例3:异常值对方差的影响
场景:实验组数据含异常值[10, 12, 11, 13, 1000]。
- 原始方差(无异常):σt2=2.5
- 含异常方差:σt2=194928(极端高估)
- 处理:截断异常值(如阈值=20),修正后数据为[10,12,11,13,20],方差恢复合理范围。
关键结论
- 绝对差方差:直接相加各组方差,需满足正态性。
- 相对差方差:用Delta方法近似,避免比率分布复杂性。
- 比率类指标:需匹配分析单元(如用户级拆分),否则需调整协方差项。
- 异常值:通过截断或Bootstrap方法处理,避免方差膨胀。
七、多重测试问题
1. 什么是多重测试问题?
多重测试问题是指在AB实验中进行多次假设检验时,整体犯第一类错误(假阳性)的概率显著增加的现象。
- 核心机制:假设检验的显著性水平(α,通常设为0.05)表示单次检验中错误拒绝原假设(H0)的概率为5%。如果进行N次独立的检验:
- 所有检验都正确的概率为 (1−α)N(例如,α=0.05时,为0.95N)。
- 至少犯一次错误的概率为 1−(1−α)N,随N增加而指数级上升(例如,N=10时,错误概率约40%)。
- 后果:在AB实验中,这可能导致“假阳性”结论,例如错误地认为实验组有效(实际无效),从而做出错误决策。
- 示例:以5%显著性水平为例,N次相同检验后,错误概率从5%升至1 - 0.95N。
为什么重要?
在AB实验中,多重测试会放大噪声,导致实验结果不可靠,尤其在以下场景:
- 多次重复实验(如反复测试同一策略)。
- 多个指标或多组对比。
- 实验过程中“偷窥”数据。
2. 多重测试的来源和避免方法
多重测试在AB实验中常见,需主动避免。
来源
- 多次重复相同实验(图3-9实验A,A*,A**):例如,第一次实验无显著效果,反复重试直到某次出现“显著”,这很可能由随机波动导致假阳性。
- 多次进行相同对比(图3-9实验B和C):如一个实验组与多个对照组对比,或多个相同实验组与一个对照组对比。注意:不同策略的实验组不构成多重测试。
- 实验过程中多次查看结果(图3-9实验E):在数据不稳定时“偷窥”,可能偶然看到显著结果(如正向波动),导致实验过早停止。
- 同一个实验有多个指标(图3-9实验D):例如,计算100个指标时,即使实验无效,约5个指标可能随机显著(假阳性率5%)。

避免策略
- 精简指标:核心指标(如关键业务指标)数量应尽量少,避免多目标比较。
- 禁止数据偷窥:实验中途不查看结果,以最终稳定数据为决策依据。
- 实验设计规范:
- 不重复相同实验。
- 避免多余组别对比(如多个相同实验组)。
- 优先预防:文档强调“尽量避免多重测试”,因为控制方法有局限。
为什么避免优于控制?
多重测试会增加假阳性,而统计校正方法(如Bonferroni)可能过于保守,增加第二类错误(假阴性,即漏检真实效果)。因此,预防是首选。
3. 如何控制多重测试问题?
当多重测试不可避免(如实验有多个关键指标),需用统计方法控制整体错误率。文档介绍了经典方法和扩展技术,核心目标是控制整体第一类错误率(Family-Wise Error Rate, FWER)或假阳性率。
(1)基本方法:Bonferroni校正
- 原理:若进行n次检验,将显著性水平α校正为α/n。例如:
- 3个指标时,校正后α = 0.05 / 3 ≈ 0.0167。
- 决策规则:P值需≤校正后α才算显著,或直接将P值乘以n后与原始α比较。
- 优点:简单、通用,能严格控制FWER。
- 缺点:过于保守(阈值过严),可能导致真实效应被忽略(增加第二类错误)。
(2)扩展方法:应对Bonferroni的保守性
文档介绍两种改进方法,更灵活地分配α:
-
Fallback法(备用检验):
- 适用场景:指标有优先级(如主要指标和次要指标)。
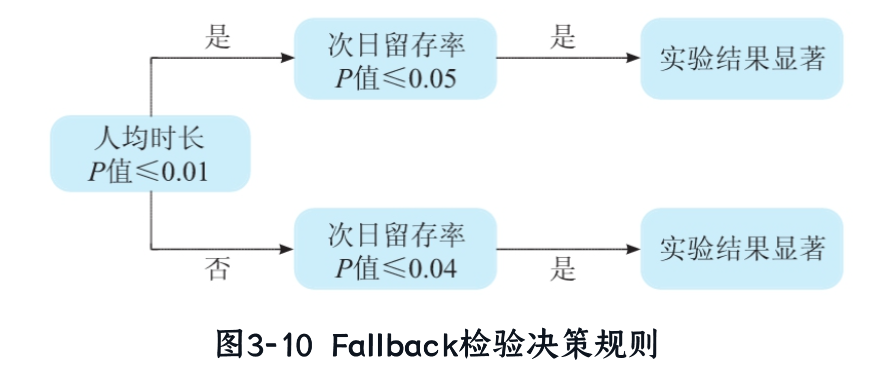
- 原理:不均匀分配α。例如:
- 第一步:检验主要指标(如用户人均使用时长),α=0.01。
- 如果显著,则次要指标(如次日留存率)用较高α(如0.05)。
- 如果不显著,则次要指标用较低α(如0.04)。
- 优点:优先保障主要指标,减少保守性。
- 示例:图3-10中,决策规则基于指标显著性动态调整阈值。
-
Holm法(逐步校正):
- 适用场景:指标有固定顺序。
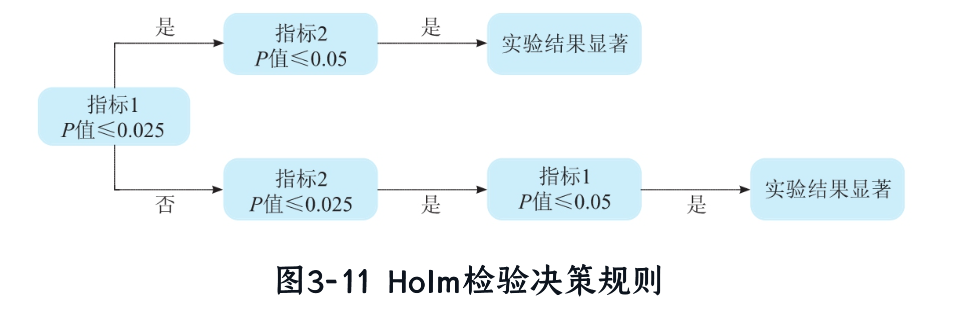
- 原理:逐步调整α。例如:
- 第一步:检验指标1,α=0.025。
- 如果显著,则指标2用α=0.05。
- 如果不显著,则指标2用α=0.025;并可回查指标1(如果P值≤0.05,则确证)。
- 优点:比Bonferroni宽松,但仍控制FWER。
- 示例:图3-11中,检验顺序影响阈值分配。
(3)经验法则:指标分组策略
- 适用场景:指标数量多(如成百上千),无法严格排序时。
- 原理:基于先验信念分组:
- 一阶指标:预计受实验影响(如核心转化率),用α=0.05。
- 二阶指标:可能受影响(如次要行为指标),用α=0.01。
- 三阶指标:不太可能受影响(如无关指标),用α=0.001。
- 贝叶斯解释:对原假设(H0)的信念越强(即认为实验无效的概率高),使用更严格的α(降低假阳性风险)。
(4)方法比较
| 方法 | 适用场景 | 优点 | 缺点 |
|---|---|---|---|
| Bonferroni | 少量指标(n较小) | 简单、严格 | 过于保守,功效低 |
| Fallback | 指标有优先级 | 灵活,减少保守性 | 需预定义指标重要性 |
| Holm | 指标有顺序 | 比Bonferroni宽松 | 顺序依赖性强 |
| 分组策略 | 大量指标 | 实用,基于业务理解 | 主观性强,需专业知识 |
4. 总结与建议
- 核心问题:多重测试在AB实验中常见,会放大假阳性风险,需在设计和分析阶段管理。
- 优先避免:减少指标数量、禁止偷窥、规范实验设计。
- 控制方法:当不可避免时,Bonferroni是基础,Fallback和Holm提供平衡,分组策略处理大规模场景。
- 关键思想:通过校正显著性水平或P值,控制整体错误率(如FWER),确保实验结论可靠。
- 文档结语:AB实验需结合方差估计、假设检验、置信区间等知识,多重测试控制是确保统计推断严谨的关键一环。
结语
AB实验的统计学原理是科学决策的基石。关键要点:
- 精度与成本平衡:样本容量、边际误差需业务权衡。
- 假设检验严谨性:P 值、功效缺一不可,避免早期偷窥。
- 实战贴士:清洗异常值、控制多重测试、优先非参数方法。
来源书籍:——刘玉凤《AB实验:科学归因于增长的利器》