【常见分布及其特征(8)】连续型随机变量-正态分布*

正态分布

引例一

1. 定义随机变量
   定义了一个连续均匀分布$U(0,1)$,并且定义了$n=5$个独立的随机变量$X_1$到$X_5$;并且均服从上述分布;即$$X_n\sim U(0,1),n=1,2,3,4,5$$
   则可以称这5个随机变量是独立同分布的

2. 抽样
   对5个随机变量执行一次抽样;
   样本值：用小写字母表示，例如一次采样后得到的具体值为 $x_1,x_2,\dots ,x_5$,其中每个 $x_i\in [0,1]$。一次采样后，样本值为:
   $$x_1=\text{Sample}(X_1),x_2=\text{Sample}(X_2),\cdots ,x_5=\text{Sample}(X_5)$$
   以下是可能的抽样结果示例,这样的示例可以举出无限多个:

示例编号	均值	$x_1$	$x_2$	$x_3$	$x_4$	$x_5$
示例 1	0.549289	0.896074	0.886996	0.374390	0.081029	0.507958
示例 2	0.419763	0.570370	0.107197	0.983434	0.221526	0.216287
示例 3	0.294898	0.185088	0.013277	0.408898	0.367660	0.499566

附一个生成的代码

import numpy as npsp = np.random.random((3,5))
print(sp)
# 对每行求均值
row_means = np.mean(sp, axis=1)
print(row_means)
print(np.column_stack((row_means, sp)))

3. 扩大随机变量,再次抽样
   $n=1000$个独立的随机变量$X_1$到$X_{1000}$;并且均服从上述分布;即$$X_n\sim U(0,1),n=1,2,3,\cdots ,1000$$

示例编号	均值	$x_1$	$x_2$	$x_3$	$\cdots$	$x_{1000}$
示例 1	0.50698297	0.84908216	0.13467754	0.374390	$\cdots$	0.06873601
示例 2	0.48454968	0.66022503	0.03217824	0.983434	$\cdots$	0.70057909
示例 3	0.49077309	0.25737745	0.04264012	0.408898	$\cdots$	0.30889889

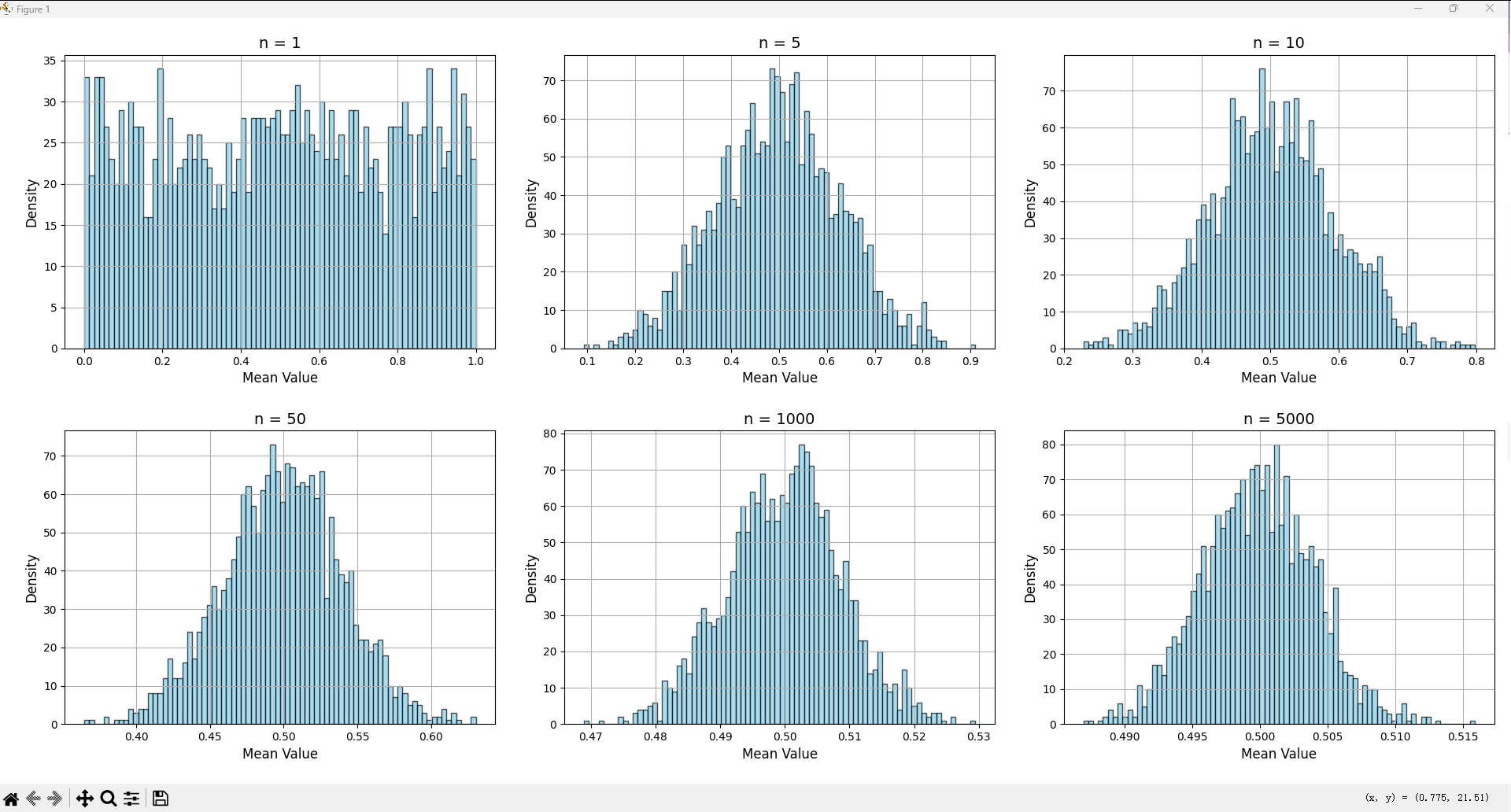
观察均值这一列,可以明显看出,当$n=5\to n=1000$,时,均值的稳定程度明显提高了,而且趋近于$X_i$的期望了;

• 如果觉得以上的不够直观,以下展示了各12组示例,第一列均为均值,均匀分布;

# n=5时的结果
[0.51177121 0.64972725 0.79864437 0.26144494 0.02885988 0.82017961]
[0.5387426  0.15816605 0.72253606 0.67549004 0.60952049 0.52800036]
[0.25243907 0.87643116 0.09397123 0.00179747 0.02647162 0.26352389]
[0.49120919 0.37110317 0.56440969 0.69843874 0.38633834 0.43575599]
[0.49709079 0.96020927 0.6040899  0.60171813 0.05464104 0.26479562]
[0.56874528 0.15495668 0.72611065 0.6985964  0.61305459 0.65100806]
[0.56970291 0.21338898 0.72839761 0.26438999 0.98735146 0.6549865 ]
[0.57184459 0.56795882 0.53453043 0.59070316 0.75968399 0.40634656]
[0.67773425 0.91024391 0.85876042 0.70395502 0.10358019 0.81213171]
[0.64856283 0.57525252 0.87790623 0.49302471 0.31732044 0.97931024]
[0.37102274 0.65237646 0.55096309 0.44173061 0.07955758 0.13048595]
[0.4822816  0.47407257 0.21329814 0.27420517 0.98064111 0.46919102]# n=1000时的结果
[0.4945074  0.50273574 0.52522912 ... 0.38031662 0.42860546 0.72074343]
[0.49621251 0.67881337 0.03880736 ... 0.92981839 0.65805523 0.38261631]
[0.49262885 0.81203807 0.43174388 ... 0.68740689 0.92866097 0.56505152]
[0.50967169 0.14997624 0.93324006 ... 0.53000919 0.48711552 0.26967198]
[0.49939796 0.63793338 0.87528609 ... 0.98436646 0.91608776 0.32658811]
[0.50291407 0.32440555 0.03177322 ... 0.96926983 0.52440474 0.73910828]
[0.50908082 0.88887095 0.46454131 ... 0.04160692 0.63408981 0.72006609]
[0.5006352  0.25307945 0.5568652  ... 0.96087729 0.10194726 0.54255956]
[0.49424821 0.08349161 0.35183987 ... 0.22038619 0.93989811 0.14642372]
[0.48437207 0.4528952  0.91680597 ... 0.20512634 0.19849493 0.53023536]
[0.49658921 0.92238767 0.17093952 ... 0.71290388 0.41343221 0.18931387]
[0.49429535 0.96498261 0.81471275 ... 0.93917227 0.84554065 0.59315527]

• 不同的$n$绘制分布图像如下,可见随着n的增大,图像趋向于一个钟形曲线;
  

4. 其他分布抽样
   若随机变量服从指数分布呢?设$X_i\sim \text{Exp}(2)$
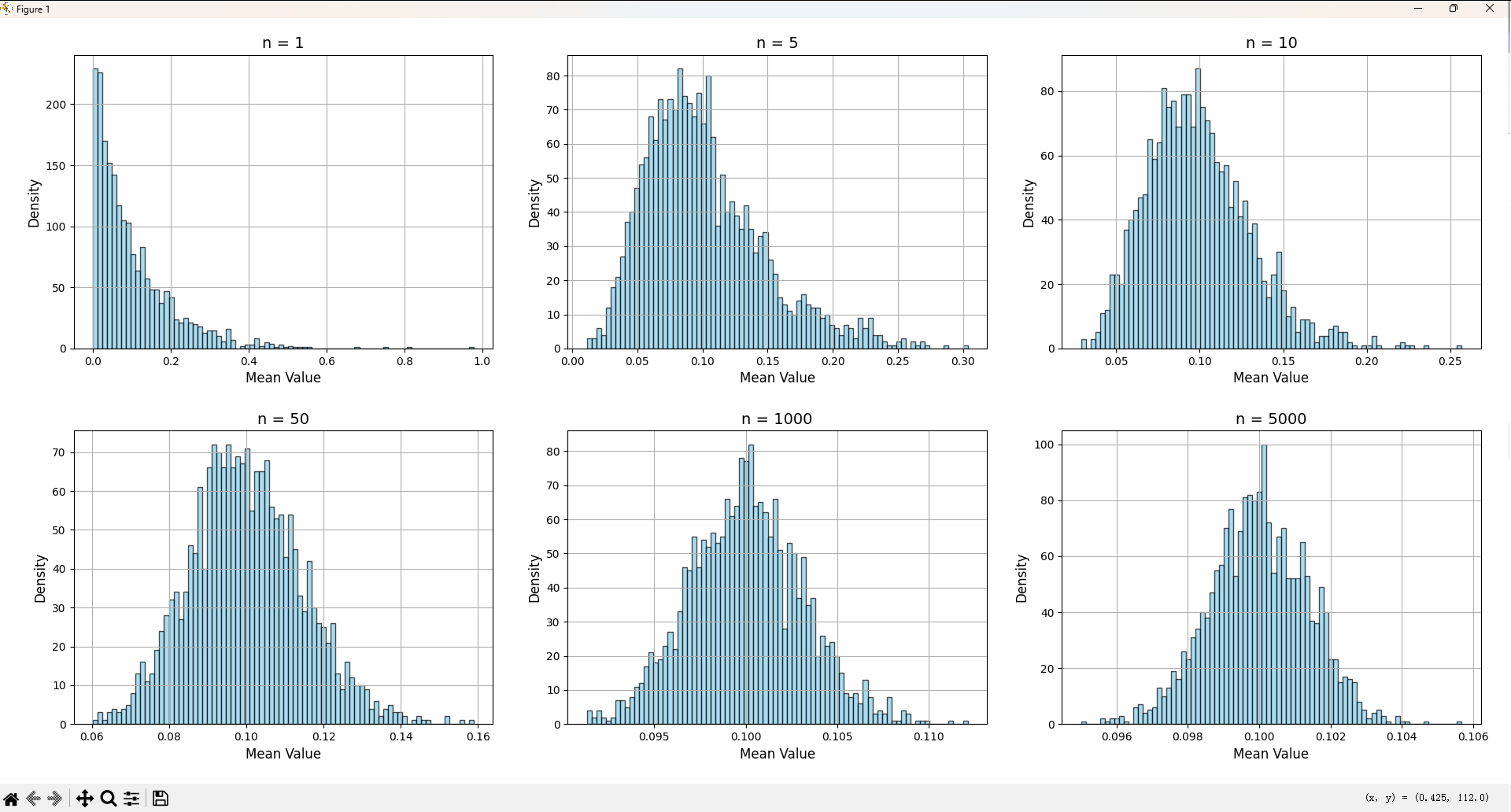
   执行相同的采样方式,可见,同样伴随着n的增大,$均值$这一列的稳定性提高了,且都趋向于$X_i$的期望

# n=5时的结果
[0.73411466 0.70151055 0.58552744 1.40848118 0.52992534 0.44512879]
[0.81113348 0.53431281 0.27084777 0.64021452 0.17419464 2.43609766]
[0.40670354 0.28069173 0.09011335 0.46911745 0.77372054 0.4198746 ]
[0.39217388 0.71925745 0.33419681 0.14974111 0.43873465 0.31893941]
[1.10752828 0.91971051 1.88885734 0.78719437 1.72043777 0.22144144]
[0.66299886 0.53282981 0.52905482 0.51776715 1.00682295 0.72851959]
[0.52414378 0.55970346 1.30554564 0.35656776 0.16566018 0.23324187]
[0.74790822 0.15209213 1.45643592 0.00856253 1.65698463 0.4654659 ]
[0.47633977 0.08690879 0.7636792  0.09175103 0.91023342 0.52912641]
[0.24892092 0.11581998 0.58664384 0.07320079 0.35082388 0.11811614]
[0.76317128 0.18174787 1.81766939 0.37271795 0.9385246  0.50519659]
[0.28458274 0.54393585 0.21895033 0.05139447 0.22892284 0.37971021]# n=1000时的结果
[0.50554701 0.12433105 0.1030619  ... 0.29139791 0.14156148 0.62659368]
[0.47398597 0.63052295 0.19590248 ... 0.01708745 0.18198675 0.15249499]
[0.49456711 0.24362464 0.47198712 ... 0.01233769 0.10306549 0.01969198]
[0.50014714 0.01423834 0.02672236 ... 1.41039619 0.18627241 0.91300211]
[0.50806173 0.14285735 0.13048108 ... 1.02997043 1.37381383 0.06590316]
[0.49356967 0.12188426 0.00758442 ... 0.09492193 0.08728697 0.42673882]
[0.49165601 0.2808061  2.53125083 ... 0.23595166 0.56993227 0.03543   ]
[0.48882824 1.13584049 0.19034411 ... 0.03731577 0.14899468 0.11803879]
[0.51453059 0.20444391 0.45787545 ... 1.06898298 0.68646825 0.08849507]
[0.49986363 0.43790124 1.82583125 ... 2.76173303 0.6031149  0.13847748]
[0.51533877 0.02963715 0.1906024  ... 0.84861804 0.50370152 0.75360766]
[0.49119387 1.24506202 2.57919455 ... 0.04874295 0.9975069  0.14039345]

附生成代码

sp = np.random.exponential(scale=0.5, size=(6,1000))
# print(sp)
# 对每行求均值
row_means = np.mean(sp, axis=1)
# print(row_means)
print(np.column_stack((row_means, sp)))

• 不同的$n$绘制分布图像如下,可见随着n的增大,图像和均匀分布一样,也同样趋向于一个钟形曲线;实际可尝试不同分布,都会趋向这个曲线,只是收敛的速度有快有慢;
  
• 附绘图代码

# 独立同分布中心极限定理
import randomimport numpy as np
from matplotlib import pyplot as plt
import math# 设置抽样次数固定
samplingNumber = 2000# 设置多个不同的样本容量n值
sampleSizes = [1,5, 10, 50, 1000, 5000]# 计算接近正方形的布局
n_plots = len(sampleSizes)
cols = math.ceil(math.sqrt(n_plots))
rows = math.ceil(n_plots / cols)# 创建子图布局
fig, axes = plt.subplots(rows, cols, figsize=(cols * 5, rows * 4))# 如果只有一个子图，则需要确保axes可迭代
axes = axes.flatten()[:n_plots]for ax, sampleSizeN in zip(axes, sampleSizes):# 生成随机数矩阵，并计算每行的均值# sampling = np.random.rand(samplingNumber,sampleSizeN)# sampling = np.random.poisson(lam=0.5, size=(samplingNumber,sampleSizeN))sampling = np.random.exponential(scale=0.1, size=(samplingNumber,sampleSizeN))# sampling = np.random.binomial(n=10, p=0.5, size=(samplingNumber, sampleSizeN))row_means = np.mean(sampling, axis=1)# 在对应的子图上绘制直方图ax.hist(row_means, bins=80, density=False, alpha=0.7, color='skyblue', edgecolor='black')# 子图标题ax.set_title(f'n = {sampleSizeN}', fontsize=14)ax.set_xlabel('Mean Value', fontsize=12)ax.set_ylabel('Density', fontsize=12)ax.grid(True)# 调整子图之间的距离
plt.tight_layout()# 显示图形
plt.show()

6. 均值的分布
   如我们将均值这一栏看作是一个随机变量$M_n$,那么$M_n$的定义应该为:
   $$M_n=\frac{1}{n}(X_1+X_2+\cdots +X_n)=\frac{1}{n}\sum _{i=1}^n{X}_i$$
   是否可以写出此随机变量的分布函数?实际此分布就是正态分布;

引例二

现在有一个均匀的六面骰子,定义随机变量$X$,表示掷出的骰子点数;
定义一个试验:连续投出100次,结果分别是不确定值,使用随机变量:$X_1,X_2,X_3,\cdots ,X_{100}$;表示;(注意,因为没有实际的抛出,故而并不是某个确定值,骰子没有变,故而所有的随机变量均服从同一个离散的均匀分布);
那么定义一个新的随机变量:$\bar{X}$,表示上述一组随机变量的均值;就称为样本均值;注意:样本均值也是一个随机变量(随机变量的均值也是一个随机变量);
$$\bar{X}=\frac{1}{n}\sum _{i=0}^n{X}_i$$
既然是随机变量,那么就应该有概率分布;对于任意的一组独立同分布的随机变量(有限的均值和方差),无论初始分布如何,只要样本数量足够大,即$n\to \infty$,他的样本均值的概率分布都应该近似服从正态分布(中心极限定理);

随机变量实际是一个函数映射,事件的实际结果和实数关联起来的函数;
但随机变量更容易的理解为就是一个不确定的数,就是一个未知数,取值的范围就是映射函数的值域;它表示一种不确定的结果,表示抛出一个硬币的正反结果,表示骰子的点数,表示一个电容的寿命,可以表示一切不确定的结果;所以实际可以理解为是一个未知数;
何时未知数变化为一个确定的值呢?即当硬币落地,骰子出现点数时;$X$变化为了$x$,即从一个不确定值,变为了一个确定的值,称为一次抽样,显然对于同一个随机变量可以进行多次抽样,从而获取不同的抽样结果;
$$x_1=\text{Sample}(X),x_2=\text{Sample}(X),$$
我们可以将抛出一枚硬币的的结果定义为随机变量$X$;
那么抛出一枚硬币100次的结果也可以定义为单个随机变量$X$,表示落到正面的次数,当然我们可以有其他的定义方式,比如定义100个随机变量,表示每一次的结果是正面还是反面$X_1,X_2,X_3,\cdots ,X_{100}$;并且这100个随机变量是独立同分布的;
当我实际抛出100次时,随机变量变为实际的确定值,那么就这么表示:
$x_1,x_2,x_3,\cdots ,x_{100}$,其中$x_1=1,x_2=0,\cdots$;
如果我抛出100个硬币的行为,执行2次采样呢?
我同样使用100个随机变量来表示;那么可能的结果可以表示为:
$x_1^1,x_2^1,x_3^1,\cdots ,x_{100}^1$
$x_1^2,x_2^2,x_3^2,\cdots ,x_{100}^2$
也可以表示为:
$x_{1,1},x_{2,1},x_{3,1},\cdots ,x_{100,1}$
$x_{1,2},x_{2,2},x_{2,3},\cdots ,x_{100,2}$
就是一种表示数据的形式,乐意的话:用画个表格,或者用二维矩阵表示也可以

定义

若连续型随机变量$X$的概率密度函数为:
$$\boxed{f(x)=\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}}}$$
其中$\mu ,\sigma >0$为常数则称$X$服从参数为$\mu ,\sigma$的正态分布或高斯分布;
$$\boxed{X\sim N(\mu ,{\sigma }^2)}$$
对应的累积分布函数为:
$$\boxed{F(x)={\int }_{-\infty }^x\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{(t-\mu {)}^2}{2{\sigma }^2}}dt}$$

• 特殊的,当$\mu =0,\sigma =1$时,即$N(0,1)$称为标准正态分布
  此时的概率密度函数和累积分布函数特殊的记为,即令:$\mu =0,\sigma =1$:
  $$\boxed{\phi (x)}=f(x)=\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}}=\frac{1}{\sqrt{2\pi }}{e}^{-x^2/2}$$
  $$\boxed{\Phi (x)}=F(x)={\int }_{-\infty }^x\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{(t-\mu {)}^2}{2{\sigma }^2}}dt=\frac{1}{\sqrt{2\pi }}{\int }_{-\infty }^x{e}^{-t^2/2}dt$$

参数

正态分布有2个参数,$\mu ,{\sigma }^2$分别表示分布的期望和标准差;
可自己调整参数看看概率密度函数的变化(卡的话把下面的累积分布函数关闭,有积分会卡一些):正态分布

可以明显的看出:

• 这个钟形曲线,的中心就是期望,也就是$\mu$,且关于$x=\mu$对称;
• $\sigma$关系着曲线的陡峭程度,$\sigma$越小则越尖,即分布越集中,反之;
• $x=\mu$时,取到最大值
  $$f(\mu )=\frac{1}{\sqrt{2\pi }\sigma }$$

分布特征值

由定义易知正态分布的:

• 期望
  $$E(X)=\mu$$
• 方差
  $$\text{Var(X)}={\sigma }^2$$

引理

任意一个服从正态分布的随机变量都可以通过线性变换为标准正态分布;
设随机变量$X\sim N(\mu ,{\sigma }^2)$;
已知标准正态分布的期望为0,标准差为1,累积分布函数为$\Phi (x)$;
设新的随机变量$Z\sim N(0,1)$,设:
$$Z=\frac{X-\mu }{\sigma }$$

证明期望为0,即
$$\begin{array}{rl}E(Z)& =E(\frac{X-\mu }{\sigma })\\ & =E[\frac{1}{\sigma }(X-\mu )]\\ & =\frac{1}{\sigma }E[(X-\mu )]\\ & =0\end{array}$$

证明方差为1,即
$$\begin{array}{rl}\text{Var}(Z)& =\text{Var}(\frac{X-\mu }{\sigma })\\ & =\text{Var}[\frac{1}{\sigma }(X-\mu )]\\ & =\frac{1}{{\sigma }^2}\text{Var}[(X-\mu )]\\ & =\frac{1}{{\sigma }^2}\text{Var}(X)\\ & =\frac{1}{{\sigma }^2}{\sigma }^2\\ & =1\end{array}$$

由期望性质
$$E(aX)=aE(X)$$
可得方差性质
$$\begin{array}{rl}\text{Var}(aX)& =E[(aX{)}^2]-[E(aX){]}^2\\ & =E(a^2{X}^2)-[aE(X){]}^2\\ & =a^{2}E(X^2)-a^{2}E(X{)}^2\\ & =a^2[E(X^2)-E(X{)}^2]\\ & =a^2\text{Var}(X)\end{array}$$
即
$$\boxed{\text{Var}(aX)=a^2\text{Var}(X)}$$

• 将原随机变量通过$Z=\frac{X-\mu }{\sigma }$的线性变换处理后，称为标准化（Standardization），也即Z-score 变换。此过程使数据的均值为 0、标准差为 1。
• 若原始数据服从正态分布，则标准化后的数据服从标准正态分布（均值为 0，标准差为 1 的正态分布）；否则，仅调整均值和标准差，分布形态不变。
• 请注意一下,并不是将数据缩放到一个固定区间,例如$[-0.5,0.5]$,但是如原始分布服从正态分布,则数据的取值范围通常集中在 $[-3,3]$ 之间,这是由正态分布本身影响的;若数据中存在离群点，则标准化后的值可能超出$[-3,3]$ 范围。
• Z-score 标准化是一种线性变换（减去均值、除以标准差），不改变数据的分布形态（如偏态、长尾特性）。离群点在标准化后仍然存在，但其数值大小会反映其距离均值的标准差数（例如，离群点的 Z-score 可能远大于 3 或小于 -3）。若观察分布图像，形态保持不变，仅数值比例被调整。

对于正态分布,数据的分布有68-95-99.7的规律。即数据大约有68%落在μ±σ范围内，95%在μ±1.96σ（约2σ）范围内，99.7%在μ±3σ范围内

例题

一液温调节器,设定温度为$d$°C,液体的温度为随机变量$X$(°C),且$X\sim N(d,0.5^2)$;¹
(1):$d=90$°C时,求$X$小于89°C的概率;
(2):要求保持液体的温度至少为80°C的概率不低于0.99,则$d$至少为多少?

解(1):
由题意知:
$$X\sim N(90,0.5^2)$$
使用累积分布函数计算(我拿计算器算的):
$$P(X<89)={\int }_{-\infty }^{89}\frac{1}{\sqrt{2\pi }\cdot 0.5}{e}^{\frac{(t-90{)}^2}{2\cdot 0.5^2}}dt\approx 0.2275$$
或使用标准正态分布查表:

• 设随机变量$Z$
  $$\begin{array}{c}Z=\frac{X-\mu }{\sigma }\\ X=Z\sigma +\mu \end{array}$$
  $$\begin{array}{rl}P(X<89)& =P(Z\sigma +\mu <89)\\ & =P(Z<\frac{89-\mu }{\sigma })\\ & =P(Z<\frac{89-90}{0.5})\\ & =P(Z<-2)\\ P(X<89)& =1-\Phi (2)=0.228\end{array}$$
• 或者写为
  $$\begin{array}{rl}P(X<89)& =P(\frac{X-\mu }{\sigma }<\frac{89-\mu }{\sigma })\\ & =P(\frac{X-89}{0.5}<\frac{89-89}{0.5})\\ & =\Phi (-2)\\ P(X<89)& =1-\Phi (2)=0.228\end{array}$$
  (2): 由题意知:
  $$X\sim N(d,0.5^2)$$
  求$d$最小值,要使得
  $$P(X>80)>0.99$$

$$\begin{array}{rl}P(X>80)& \\ P(X>80)& =P(Z\sigma +\mu >80)\\ & =P(Z>\frac{80-\mu }{\sigma })\\ & =P(Z<\frac{80-d}{0.5})\\ P(X>80)& =\Phi (\frac{80-d}{0.5})>0.99\end{array}$$
查表可知 $\Phi (2.33)=0.9901$,故
$$\begin{array}{rl}\frac{80-d}{0.5}& >2.33\\ d& >81.168\end{array}$$

---

1. 概率论与数理统计,浙江大学 ↩︎