算法基础——二分查找

https://www.geeksforgeeks.org/dsa/binary-search/

算法介绍

二分查找算法是一种在已排序数组中，通过将搜索区间反复划分为两半的搜索算法。二分查找的思想是利用数组已排序的信息，将时间复杂度降低到 O(log N)

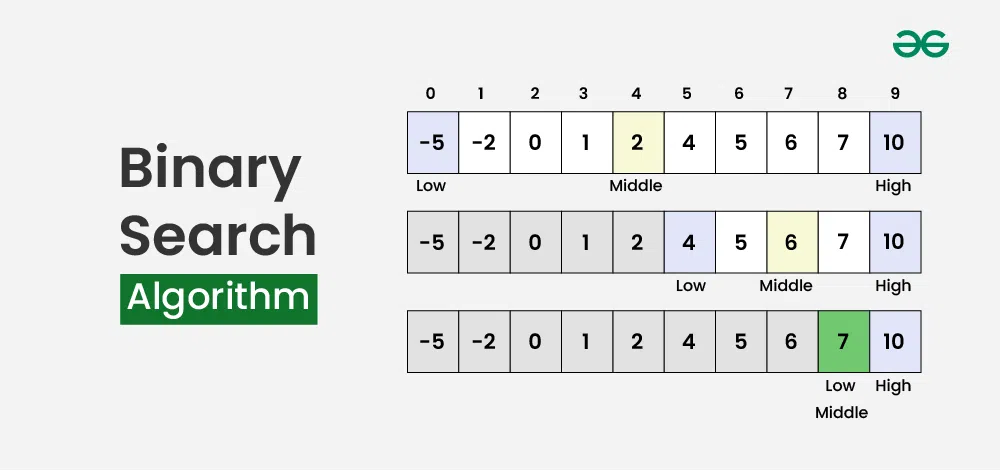
有两种方法实现二分查找 (迭代和递归)

代码实现

迭代法 ☆☆☆☆☆

下面这段代码在面试考察时希望可以做到肌肉记忆

 private  int binarySort(int[] nums, int target) {int n = nums.length;int left = 0, right = n - 1;while (left <= right) {int mid = left + (right - left) / 2;if (nums[mid] == target) return mid;else if (nums[mid] < target) left = mid + 1;else right = mid - 1;}return -1;}

1 为什么left <= right 而不是 left < right?

假设nums数组元素如下，target为 20，预期返回1

index	0	1	2	3	4
value	10	20	30	40	50
初始值	left = 0	right = 4
第一次执行	left = 0	right = 4	mid = 0+（4-0）/2 =2	nums[mid] > 20, right = mid -1 =1
第二次执行	left = 0	right = 1	mid = 0+（1-0）/2 =0	nums[mid] < 20, left = mid +1 =1
第三次执行	left = 1	right = 1	mid = 1+（1-1）/2 =1	nums[mid] = 20, 返回1

如上表格所示，如果 left < right就停止比较，那么第三次就不会执行了自然找不到索引为1，而是直接返回 -1，这和预期不符

2 为什么有些算法题中出现 left < right?

• 如果你要找某个 具体数值的位置：用 low <= high
• 如果你要找某个 边界 / 极值：用 low < high 更安全（边界不容易越界）

这里我们通过一个题目来加深理解

给定一个非递减排序的数组 nums 和一个目标值 target，返回第一个 大于等于 target 的元素索引。如果不存在，返回 nums.length

int lowerBound(int[] nums, int target) {int low = 0, high = nums.length;  // 注意这里是 high = nums.length，不是 length - 1while (low < high) {int mid = low + (high - low) / 2;if (nums[mid] < target) {low = mid + 1;  // 排除左侧} else {high = mid;     // mid 可能是解，保留它}}return low;
}

递归法 ☆☆☆

private static int binarySort2(int[] nums, int left, int right, int target) {if (left <= right) {int mid = left + (right - left) / 2;if (nums[mid] == target) return mid;else if (nums[mid] < target) return binarySort2(nums, mid + 1, right, target);else return binarySort2(nums, left, mid - 1, target);}return -1;}public static void main(String[] args) {int[] nums = {0, 1, 2, 3, 4, 5};System.out.println(binarySort2(nums, 0, nums.length - 1, 2));}