人工智能之数学基础：频率和概率之间的关系

本文重点

在前面的课程中我们学习了事件，每个事件可以包含多个多个结果，我们是否可以使用一个指标来衡量一个事件发生的可能性？这个指标就是概率，而概率来自于频率，所以本文将先介绍频率，然后介绍概率。

频率的定义

设A是一个事件，在相同的条件下进行n次实验，A发生了m次。则称m为事件A在n次实验中发生的频数或次数，称m与n之比m/n为事件A在n次实验中发生的频率，即为fn（A）

频率的稳定性和概率

当实验次数n充分大时，事件的频率总在一个定值附近摆动，而且，试验次数越多，这种摆动的幅度越小。这一性质称为频率的稳定性。当稳定到一定程度的时候，频率就会无限接近概率。所以我们可以认为，概率是通过频率来度量的，频率是概率的近似，概率是频率某种意义下的极限。

频率的性质

1. 0≤fn(A)≤1
2. fn(Ω)=1,fn(Ø)=0
3. 如果事件A1，A2，...,Ak两两互斥（任何两个事件之间都是互斥的），则所有事件并集的频率等于：

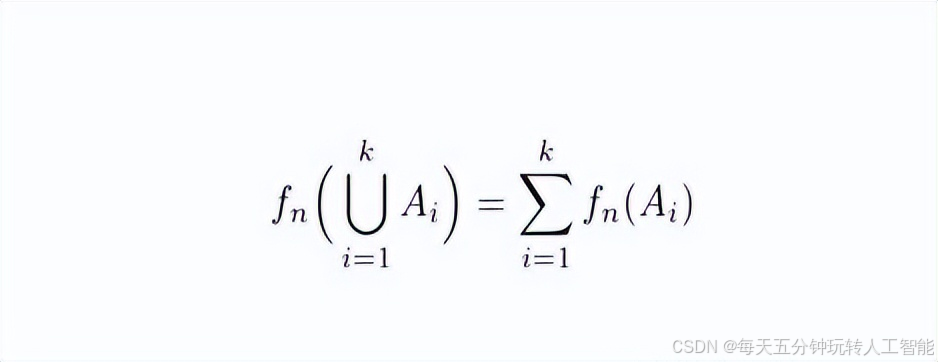
概率的定义

设E是随机实验，Ω是这个随机实验的样本空间，对Ω中的每个事件A，定义一个实数P(A)与之对应，若事件的函数P(A)满足下面的三个条件：

1. 对每个事件A，均有P(A)≥0
2. p(Ω)=1
3. 若事件A1，A2，...两两互斥（概率