当前位置：首页 > news >正文

机器学习第二课之逻辑回归（一）LogisticRegression

news 2025/8/2 5:43:20

简介：

在机器学习的知识版图中，逻辑回归是衔接线性回归与分类任务的重要桥梁。逻辑回归正是为二分类任务量身打造的利器。它巧妙借用线性回归的框架，通过 Sigmoid 函数的 “魔法转换”，将连续的预测值压缩到 0-1 之间，精准输出事件发生的概率，让决策更具可解释性。解析 Sigmoid 函数如何实现从线性到概率的跨越，探讨损失函数为何选择对数损失而非均方误差。同时，我们也会结合实际案例，展示逻辑回归在金融、医疗等领域的强大应用。无论你是刚入门机器学习的新手，还是想夯实算法基础的学习者，这节课都将带你掌握逻辑回归的核心思想，为后续深入学习更复杂的分类算法打下坚实基础。

1.逻辑回归介绍

逻辑回归（Logistic Regression）是机器学习中的⼀种分类模型，逻辑回归是⼀种分类算法，虽然名字中带有回归，但是是一个分类任务算法。由于算法的简单和⾼效，在实际中应⽤⾮常⼴泛。

1.逻辑回归的应⽤场景

⼴告点击率
是否为垃圾邮件
是否患病
⾦融诈骗
虚假账号

看到上⾯的例⼦，我们可以发现其中的特点，那就是都属于两个类别之间的判断。逻辑回归就是解决⼆分类问题的利器。

2 .逻辑回归的原理

要想掌握逻辑回归，必须掌握两点：逻辑回归中，其输⼊值是什么、如何判断逻辑回归的输出。

2.1.输⼊

$z=w{_1{}}x{_1{}}+w{_2{}}x{_2{}}+.....+w{_n{}}x{_n{}}+b$

逻辑回归的输⼊就是⼀个线性回归的结果。

2.2.激活函数

sigmoid函数:

$\sigma (Z)=\frac{1}{1+e^-z{}}$

判断标准

回归的结果输⼊到sigmoid函数当中
输出结果：[0, 1]区间中的⼀个概率值，默认为0.5为阈值

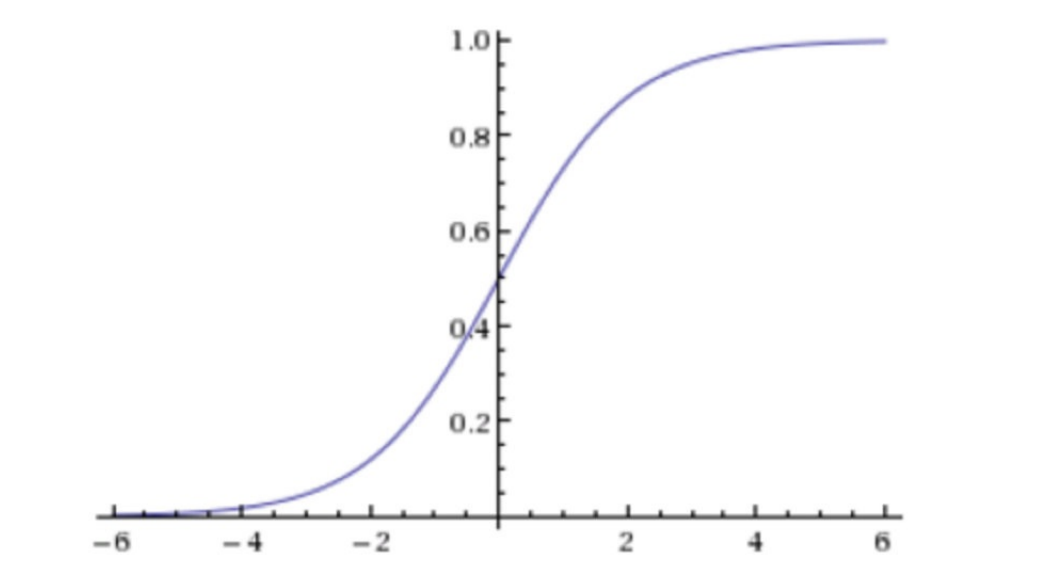
逻辑回归最终的分类是通过属于某个类别的概率值来判断是否属于某个类别，并且这个类别默认标记为1(正例), 另外的⼀个类别会标记为0(反例)。（⽅便损失计算

输出结果解释(重要)：假设有两个类别A，B，并且假设我们的概率值为属于A(1)这个类别的概率值。现在有⼀个样本的输⼊到逻辑回归输出结果0.55，那么这个概率值超过0.5，意味着我们训练或者预测的结果就是A(1)类别。那么反之，如果得出结果为0.3那么，训练或者预测结果就为B(0)类别。

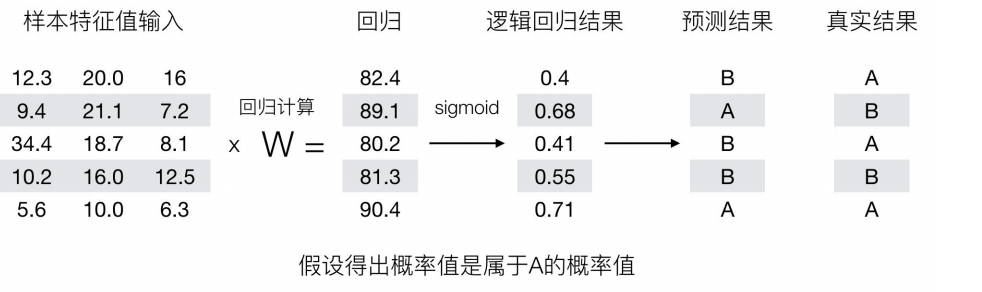
关于逻辑回归的阈值是可以进⾏改变的，⽐如上⾯举例中，如果你把阈值设置为0.6，那么输出的结果0.55，就属于B 类。 在之前，我们⽤最⼩⼆乘法衡量线性回归的损失 ,在逻辑回归中，当预测结果不对的时候，我们该怎么衡量其损失呢

我们来看下图(下图中，设置阈值为0.6)，

那么如何去衡量逻辑回归的预测结果与真实结果的差异呢

2.3.损失

逻辑回归的损失，称之为对数似然损失，公式如下：

分开类别

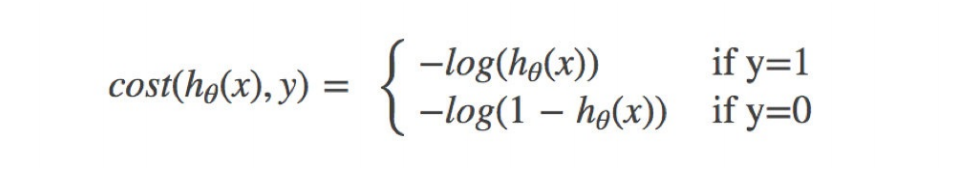
其中y为真实值，hθ(x)为预测值

怎么理解单个的式⼦呢？这个要根据log的函数图像来理解

⽆论何时，我们都希望损失函数值，越⼩越好

分情况讨论，对应的损失函数值：

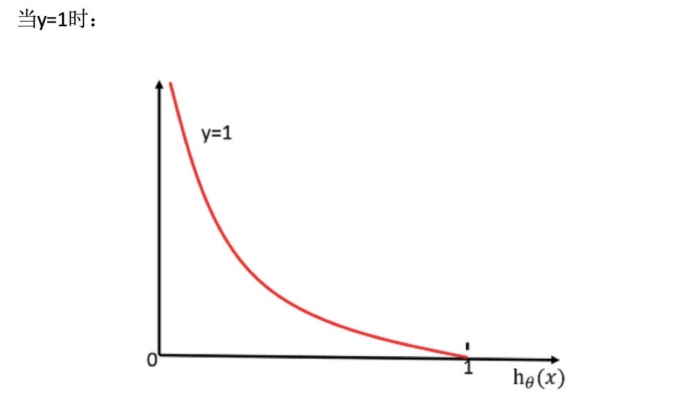
当y=1时，我们希望hθ(x)值越⼤越好；
当y=0时，我们希望hθ(x)值越⼩越好
综合完整损失函数

$\cos (h_{\theta }(x),y)=\sum_{i=i}^{m}-y_{i}\log (h_{\theta }(x))-(1-y_{i})\log (1-h_{\theta }(x))$

接下来我们呢就带⼊上⾯那个例⼦来计算⼀遍，就能理解意义了。

我们已经知道，-log(P), P值越⼤，结果越⼩，所以我们可以对着这个损失的式⼦去分析

2.4.优化

使⽤梯度下降优化算法，去减少损失函数的值。这样去更新逻辑回归前⾯对应算法的权重参数，提升原本属于1类 别的概率，降低原本是0类别的概率

对于梯度下降优化算法之前我并没有提过，因为刚学机器学习我不想一下说那么复杂，现在我就稍微讲述一下什么是梯度下降优化算法。只是简单说明一下，后面学习深度学习还会继续详细提到。

2.梯度下降⽅法介绍

1.什么是梯度下降

梯度下降法的基本思想可以类⽐为⼀个下⼭的过程。

假设这样⼀个场景：

⼀个⼈被困在⼭上，需要从⼭上下来(i.e. 找到⼭的最低点，也就是⼭⾕)。但此时⼭上的浓雾很⼤，导致可视度很低。因此，下⼭的路径就⽆法确定，他必须利⽤⾃⼰周围的信息去找到下⼭的路径。这个时候，他就可以利⽤梯度下降算法来帮助⾃⼰下⼭。具体来说就是，以他当前的所处的位置为基准，寻找这个位置最陡峭的地⽅，然后朝着⼭的⾼度下降的地⽅⾛（同理，如果我们的⽬标是上⼭，也就是爬到⼭顶，那么此时应该是朝着最陡峭的⽅向往上⾛）。然后每⾛⼀段距离，都反复采⽤同⼀个⽅法，最后就能成功的抵达⼭⾕。

梯度下降的基本过程就和下⼭的场景很类似。

⾸先，我们有⼀个可微分的函数。这个函数就代表着⼀座⼭。我们的⽬标就是找到这个函数的最⼩值，也就是⼭底。根据之前的场景假设，最快的下⼭的⽅式就是找到当前位置最陡峭的⽅向然后沿着此⽅向向下⾛，对应到函数中，就是找到给定点的梯度 ，然后朝着梯度相反的⽅向，就能让函数值下降的最快！因为梯度的⽅向就是函数值变化最快的⽅向。所以，我们重复利⽤这个⽅法，反复求取梯度，最后就能到达局部的最⼩值，这就类似于我们下⼭的过程。⽽求取梯度就确定了最陡峭的⽅向，也就是场景中测量⽅向的⼿段。

2.梯度的概念

梯度是微积分中⼀个很重要的概念

在单变量的函数中，梯度其实就是函数的微分，代表着函数在某个给定点的切线的斜率；
在多变量函数中，梯度是⼀个向量，向量有⽅向，梯度的⽅向就指出了函数在给定点的上升最快的⽅向；

在微积分⾥⾯，对多元函数的参数求∂偏导数，把求得的各个参数的偏导数以向量的形式写出来，就是梯度。

这也就说明了为什么我们需要千⽅百计的求取梯度！我们需要到达⼭底，就需要在每⼀步观测到此时最陡峭的地⽅，梯度就恰巧告诉了我们这个⽅向。梯度的⽅向是函数在给定点上升最快的向，那么梯度的反⽅向就是函数在给定点下降最快的⽅向，这正是我们所需要的。所以我们只要沿着梯度的反⽅向⼀直⾛，就能⾛到局部的最低点

3.梯度下降的相关概念

步⻓(Learning rate)：

步⻓决定了在梯度下降迭代的过程中，每⼀步沿梯度负⽅向前进的⻓度。⽤前⾯下⼭的例⼦，步⻓就是在当前这⼀步所在位置沿着最陡峭最易下⼭的位置⾛的那⼀步的⻓度。

特征(feature)：

指的是样本中输⼊部分，⽐如2个单特征的样本(x (0) , y (0)),(x (1) , y (1)),则第⼀个样本特征为x (0)，第⼀个样本输出为y (0)。

假设函数(hypothesis function)：

在监督学习中，为了拟合输⼊样本，⽽使⽤的假设函数，记为hθ(x)。⽐如对于单个特征的m个样本 (x (i) , y (i))(i = 1, 2, ...m),可以采⽤拟合函数如下：

$h_{\theta }(x)=\theta _{0}+\theta _{1x}$

损失函数(loss function)：

为了评估模型拟合的好坏，通常⽤损失函数来度量拟合的程度。损失函数极⼩化，意味着拟合程度最好，对应的模型参数即为最优参数。在线性回归中，损失函数通常为样本输出和假设函数的差取平⽅。⽐如对于m个样本(xi, yi)(i = 1, 2, ...m)，采⽤线性回归，损失函数为

$J(\theta _{0},\theta _{1})=\sum_{i=1}^{m}(h_{\theta })(x_{i}-y_{i})^{2}$

其中xi表示第i个样本特征，yi表示第i个样本对应的输出，hθ(xi)为假设函数

3.1梯度下降举例

单变量函数的梯度下降

我们假设有⼀个单变量的函数 :J(θ) = $\theta ^{2}$

函数的微分:J(θ) = 2θ

初始化，起点为： $\theta ^{0}$ = 1

学习率：α = 0.4

我们开始进⾏梯度下降的迭代计算过程:

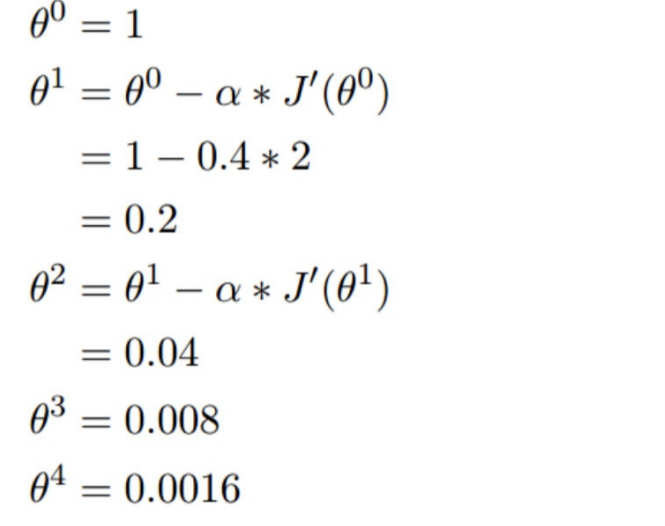
如图，经过四次的运算，也就是⾛了四步，基本就抵达了函数的最低点，也就是⼭底

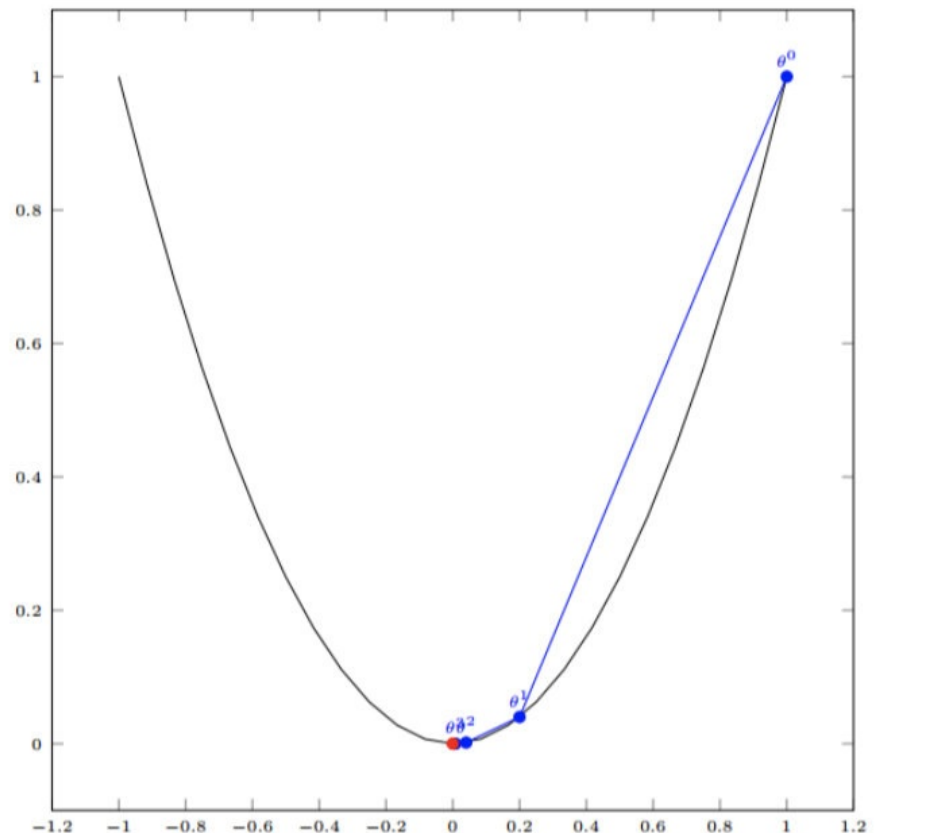
多变量函数的梯度下降

我们假设有⼀个⽬标函数：:J(θ) = $\theta _{1}^{2}$ + $\theta _{2}^{2}$

现在要通过梯度下降法计算这个函数的最⼩值。我们通过观察就能发现最⼩值其实就是 (0，0)点。但是接下来，我们

会从梯度下降算法开始⼀步步计算到这个最⼩值! 我们假设初始的起点为: θ 0 = (1, 3)

初始的学习率为:α = 0.1

函数的梯度为:▽:J(θ) =< 2 $\theta _{1}$ ,2 $\theta _{2}$ >

进⾏多次迭代:

我们发现，已经基本靠近函数的最⼩值点

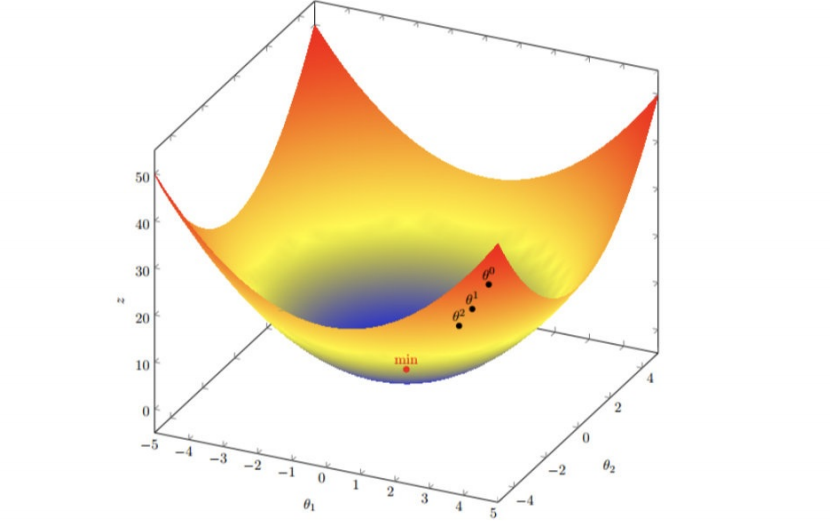
3.2 梯度下降（Gradient Descent）公式

$\theta _{i+1}=\theta _{i}-\frac{\partial }{\partial\theta _{i} }J(\theta )$

1) α是什么含义？

α在梯度下降算法中被称作为学习率或者步⻓，意味着我们可以通过α来控制每⼀步⾛的距离，以保证不要步⼦跨的太⼤扯着蛋，哈哈，其实就是不要⾛太快，错过了最低点。同时也要保证不要⾛的太慢，导致太阳下⼭了，还没有⾛到⼭下。所以α的选择在梯度下降法中往往是很重要的！α不能太⼤也不能太⼩，太⼩的话，可能导致迟迟⾛不到最低点，太⼤的话，会导致错过最低点！

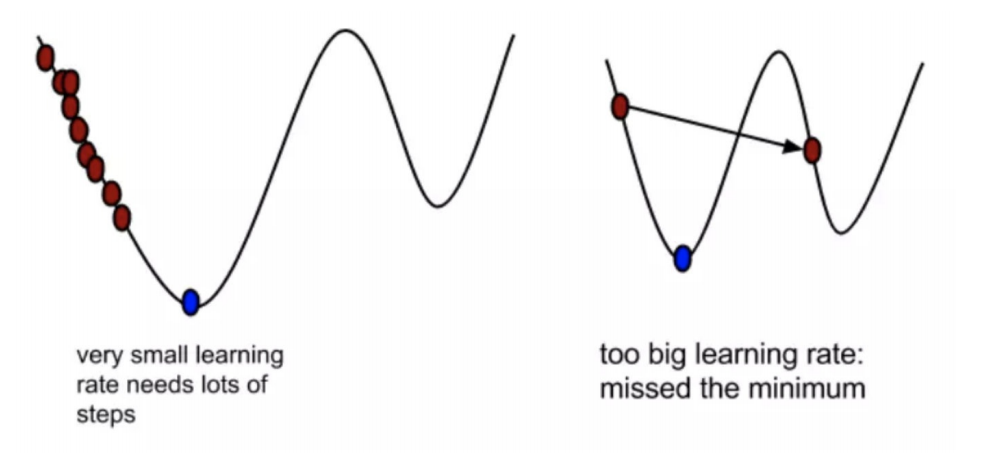
2) 为什么梯度要乘以⼀个负号？

梯度前加⼀个负号，就意味着朝着梯度相反的⽅向前进！我们在前⽂提到，梯度的⽅向实际就是函数在此点上升最快的⽅向！⽽我们需要朝着下降最快的⽅向⾛，⾃然就是负的梯度的⽅向，所以此处需要加上负号

我们通过两个图更好理解梯度下降的过程

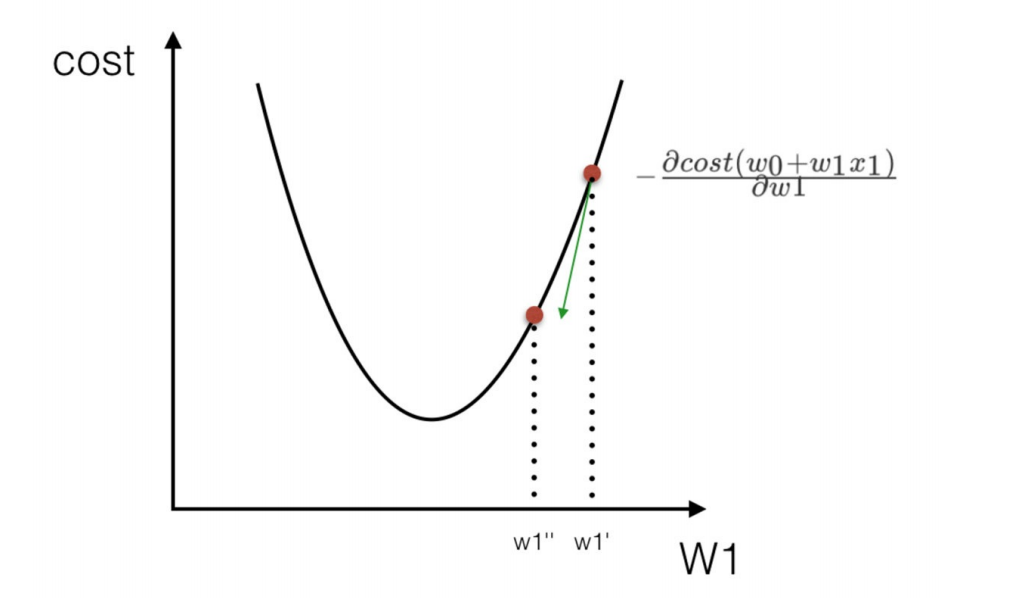
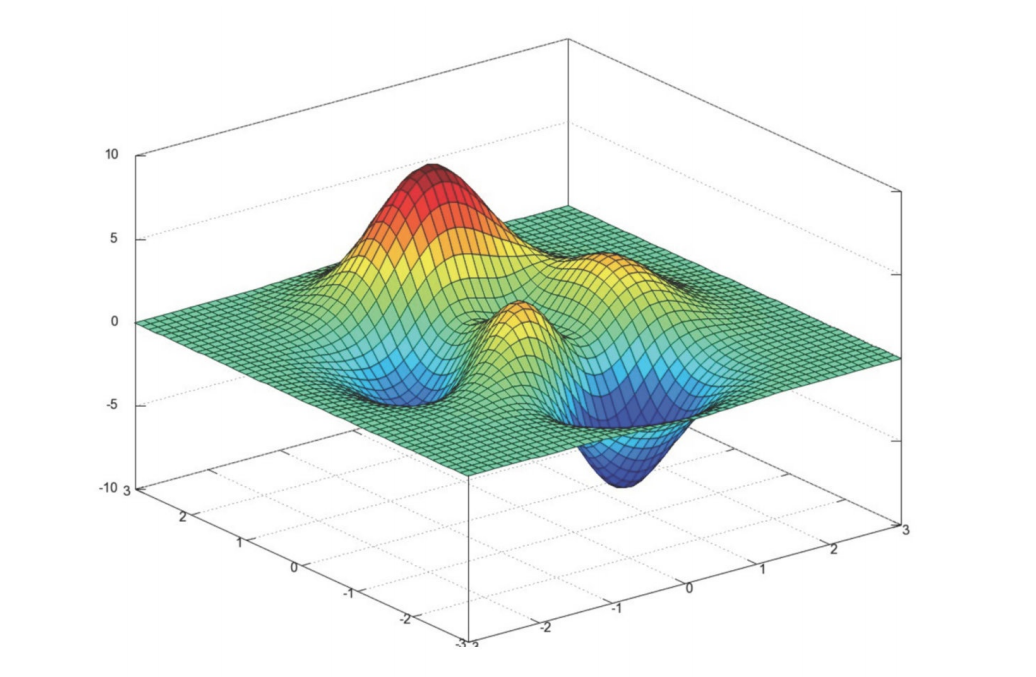
这些公式理解不了就不用专研进去，知道有这个概念就行，后面还会继续说，慢慢多讲几遍就可以理解了

3.逻辑回归api介绍

LogisticRegression(penalty='l2', dual=False, tol=0.0001, C=1.0, fit_intercept=True,intercept_scaling=1, class_weight=None, random_state=None, solver='liblinear',max_iter=100, multi_class='ovr', verbose=0, warm_start=False, n_jobs=1)

部分了解一下就行

penalty：正则化方式，有 l1 和 l2 两种。用于指定惩罚项中使用的规范。newton-cg、sag 和 lbfgs 求解算法只支持 L2 规范。L1 规范假设的是模型的参数满足拉普拉斯分布，L2 假设的模型参数满足高斯分布，所谓的范式就是加上对参数的约束，使得模型更不会过拟合（overfit），但是如果要说是不是加了约束就会好，这个没有人能回答，只能说，加约束的情况下，理论上应该可以获得泛化能力更强的结果。
dual：按默认即可。对偶方法只用在求解线性多核（liblinear）的 L2 惩罚项上。当样本数量 > 样本特征的时候，dual 通常设置为 False。
tol：float，默认值：1e-4，容许停止标准，即我们说的要迭代停止所需达到的精度要求。
C：正则化强度。为浮点型数据。正则化系数 λ 的倒数，float 类型，默认为 1.0。必须是正浮点型数。像 SVM 一样，越小的数值表示越强的正则化。
fit_intercept：指定是否应该将常量（即偏差或截距）添加到决策函数中。相当于是否加入截距项 b。默认加入。
intercept_scaling：仅在正则化项为 "liblinear"，且 fit_intercept 设置为 True 时有用。float 类型，默认为 1。
class_weight：用于标示分类模型中各种类型的权重，可以是一个字典或者 'balanced' 字符串。默认为 None，也就是不考虑权重。在出现样本不平衡时，可以通过这个参数来调整，防止算法对训练样本多的类别偏倚。
random_state：随机种子，用于控制随机数生成，确保结果可复现。
solver：优化算法选择，'liblinear' 是默认值，适用于小数据集，其他可选 'newton-cg'、'sag'、'lbfgs' 等。
max_iter：最大迭代次数，默认 100，用于控制优化算法的迭代次数。
multi_class：多分类策略，'ovr'（一对多）是默认值，其他可选 'multinomial'（多项式逻辑回归）。
verbose：日志显示模式，0 表示不输出日志，1 或 2 表示输出详细日志。
warm_start：是否重用之前的模型结果作为初始化，False 表示不重用，True 表示重用。
n_jobs：并行计算的线程数，-1 表示使用所有可用线程，1 表示不使用并行计算。

4.案例- 银行贷款

4.1.数据集分析

通过网盘分享的文件：creditcard.csv
链接: https://pan.baidu.com/s/1puCeQCFiT8M0aufcblYJCA 提取码: sh37

对于Time来说是我们训练用不到的标签，后面需要删除。

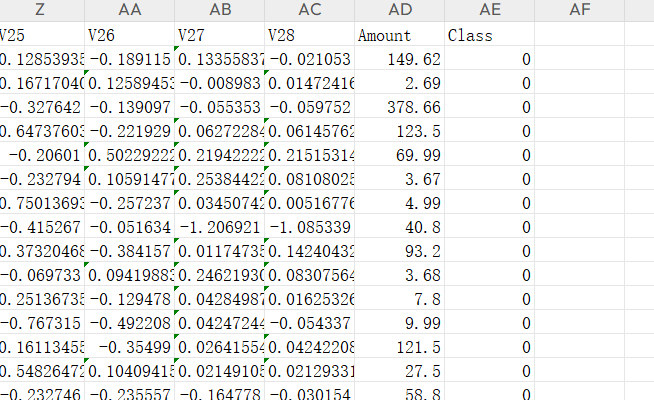
我们看到前面数据与Amount的数据数值范围不同，这就可能导致对于Amount标签会很大因素影响模型的相关系数，这就需要对这列数据进行压缩处理，也就是我们常说的标准化处理。

Z 标准化（Z-score 标准化）

Z 标准化是将数据转换为均值为 0、标准差为 1 的标准正态分布。

公式：

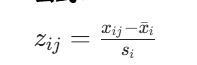
$z_{ij}$ ：标准化后的值
$x_{ij}$ ：原始数据值
$\bar{x}_{i}$ ：特征i的均值（数学期望）
$s_{i}$ ：特征i的标准差

特点：

保留了数据的原始分布形状
处理后的数据范围通常在 [-3, 3] 之间
对异常值敏感

归一化（Normalization）

归一化是将数据线性转换到 [0, 1] 区间。

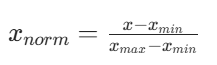
$x_{norm}$ ：归一化后的值
x：原始数据值
$x_{min}$ ：特征的最小值
$x_{max}$ ：特征的最大值

特点：

数据分布不规则或无明显分布特征
算法要求输入数据在特定范围（如神经网络的输入层）
需要消除不同特征间的量纲差异

结合前几列数据格式，所以我们应该使用 z标准化

4.2代码解析

1. 导入所需库

import pandas as pd
from  sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn import metrics

2.数据加载与预处理

data = pd.read_csv("creditcard.csv")  # 读取信用卡交易数据# 对Amount特征进行标准化处理
scaler = StandardScaler()
data["Amount"] = scaler.fit_transform(data[["Amount"]])# 删除Time特征（可能认为该特征对预测影响不大）
data = data.drop(["Time"], axis=1)

标准化处理可以让不同量级的特征处于同一尺度，有利于逻辑回归模型收敛
删除 Time 特征可能是因为时间与欺诈与否没有直接关联（或已通过 EDA 验证）

3.特征与标签分离

x = data.iloc[:, :-1]  # 取所有行，除最后一列外的所有列作为特征
y = data.iloc[:, -1]   # 取最后一列作为标签（1表示欺诈，0表示正常）

信用卡欺诈检测数据集中，标签通常是二值的：1 代表欺诈交易，0 代表正常交易

4.数据集拆分

x_train_w, x_test_w, y_train_w, y_test_w = train_test_split(x, y, test_size=0.4, random_state=100
)

将数据集按 6:4 的比例拆分为训练集和测试集
random_state=100 保证结果可复现,随机种子固定训练的数据集划分图片，避免每一次训练的图片都不一样。

5. 模型训练与评估

# 初始化逻辑回归模型，设置正则化强度C=0.01（值越小正则化越强）
estimator = LogisticRegression(C=0.01)
estimator.fit(x_train_w, y_train_w)  # 训练模型# 在训练集上的准确率
score = estimator.score(x_train_w, y_train_w)
print(score)# 对测试集进行预测并生成详细评估报告
test_predicted = estimator.predict(x_test_w)
print(metrics.classification_report(y_test_w, test_predicted))

6.运行结果

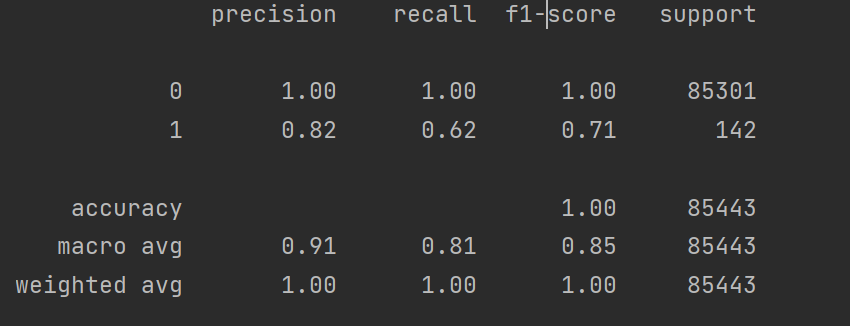
构建了一个基础的逻辑回归欺诈检测模型，适合作为入门示例。模型评估指标：仅看准确率意义不大，应重点关注召回率（识别出的欺诈样本比例）和精确率、可添加混淆矩阵、ROC 曲线和 AUC 值等评估指标。这个代码结果是以这些指标输出的，后面还会继续说关于逻辑回归的这些评价指标具体代表的含义，学习是一步一步的。

4.3.完整代码

import pandas as pd
from  sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn import metrics
import pylab as pldata=pd.read_csv("creditcard.csv")scaler=StandardScaler()
data["Amount"]=scaler.fit_transform(data[["Amount"]])
data=data.drop(["Time"],axis=1)x=data.iloc[:, :-1]
y=data.iloc[:, -1]x_train_w,x_test_w,y_train_w,y_test_w=train_test_split(x,y,test_size=0.4,random_state=100)estimator=LogisticRegression(C=0.01)
estimator.fit(x_train_w,y_train_w)
test_predicted=estimator.predict(x_test_w)
score=estimator.score(x_train_w,y_train_w)
print(score)
print(metrics.classification_report(y_test_w,test_predicted))

查看全文

http://www.lryc.cn/news/605540.html