城阳区奥赛暑假公益班第三次入门组初赛模拟赛

1

B
IPV6的地址是由128(2的六次方)个二进制位组成的。
IPV4的地址则是由32(2的四次方)个二进制位组成的。

2

D
首先来分析几个运算符的优先级。
优先级从高到低分别是
% 取余
<< 左移
& 与
^ 异或
| 或

13 % 9 = 4
表达式变为 5 << 1 | 4 ^ 4 & 7
5 << 1 = 10
表达式变为 10 | 4 ^ 4 & 7
4 & 7 = 0100 & 0111 = 0100 = 4
表达式变为 10 | 4 ^ 4
4 ^ 4 = 0100 ^ 0100 = 0
表达式变为 10 | 0
10 | 0 = 1010 | 0000 = 1010 = 10

3

C
计算步骤（从右往左处理）：
遇到操作数（数字）就压入栈。
遇到运算符，从栈中弹出两个操作数，运算结果压入栈。
重复直到表达式结束，栈中最终只剩一个值，即为结果。
4 入栈
2 入栈
/
取出栈顶两个元素 计算后为 4 / 2 = 2 2入栈
8 入栈
$-$
取出栈顶两个元素 计算后为 8 - 2 = 6 6入栈
1 入栈 3 入栈
+
取出栈顶两个元素 1 + 3 = 4 4入栈
*
取出栈顶两个元素 4 * 6 = 24 24入栈
表达式结束，栈内元素24即为答案。

4

D
不允许连续三次退栈操作
看D的操作序列，首先a进栈a出栈
然后bcdef依次进栈
f出栈e出栈d出栈才能得到序列，而此时已经连续三次出栈了，因此非法。

5

C
插入排序：每次在已经拍好的序列内找到新数应在的位置，最坏O(n^2)
冒泡排序：每一轮把要排序列的最大值冒到尾部，最坏O(n^2)
归并排序：自底向上合并有序序列，稳定O(NlogN)
快速排序：自上向下每次把基准值调整到应在的位置，并且把比基准值小的值放在基准值左侧，把比基准值大的值放在右侧，最坏情况会退化到O(n^2)，即序列原本有序的情况，并且选择最左侧或者最右侧值作为基准。

6

B
简要推导
设初始值
a = a0
b = b0
a = a ^ b → 现在 a = a0 ^ b0
b = a ^ b = (a0 ^ b0) ^ b0 = a0
a = a ^ b = (a0 ^ b0) ^ a0 = b0

7

A
首先在5个数字内选四个数字
如果选的是 0 1 2 3
由于第一位不能是 0 那么答案为 3 * 3! = 18
0 1 2 4 → 同上：18 种
0 1 3 4 → 18 种
0 2 3 4 → 18 种
1 2 3 4 → 没有 0，可以随意排列 → 4! = 24 种
因此答案为96种。

8

C
字母位有26种选择，数字为有十种选择。
因此答案为2626101010=676000

9

C
八进制转16进制 首先把八进制7042转化为2进制。
7=111
0=000
4=100
2=010
因此$(7042{)}_8=(111000100010)2$
转化为十六进制
1110 = 14 = E
0010 = 2 = 2
0010 = 2 = 2
因此十六进制为 E22

10

A
首先分析优先级
从高到低依次为
位与 &
位异或 ^
位或 |
逻辑与 &&
逻辑或 ||
因此 首先计算 a & b = 5 & 3 = 101 & 011 = 001 = 1
再计算 c ^ b = 100 ^ 011 = 111 =7
再计算 a | c = 101 ^ 100 = 101 = 5
1 || 7 && 5 = true

11

B
第一层会循环n次
第二层会循环logn次
因此复杂度是nlogn

12

B
初始时，假设第一个元素为最大值。
然后依次用剩下的每个元素与当前最大值比较，如果更大则更新最大值。
每个元素只需比较一次，共有 n−1 个元素需要比较。

13

A
第一位是符号位，剩下的七位是数字位 七位二进制位范围是0-127
当第一位0时，范围为 0 - 127
当第一位1时，范围为 -127 - 0
因此为 -127 - 127

14

B
二分检索的最坏复杂的是$\lceil lo{g}_2(n)\rceil$。

15

A 算法不仅仅是计算方法，而是一系列解决问题的清晰指令和策略机制。
B 正确
C 算法设计不仅要考虑如何得到正确的计算结果，还需要考虑时间和空间复杂度。
D 算法设计不能忽视运算时间，如果我们设计的算法时间复杂度很大，这个算法的应用价值就不大。

16

TFTFBD
（1）^ 是异或号，<< 是左移，>>是右移，两个数不完全一样，必然不为0。
（2）如果改为unsigned int，则该题中的机器数都是32位机器数。
对于某些高位有1的情况，如果x是16位机器数，x<<6会溢出，再进行x>>8高8位一定为0。
而如果x是32位机器数，x<<6不会溢出，再进行x>>8高8位可能不为0。
由于一些计算过程中机器数中的1比较少，表示一个机器数可以不用写出机器数的每一位，只需要标出其有1的位置即可。比如第i位（从0开始数）有1，就可以写1<<i，第i位和第j位有1可以记为1<<i | 1<<j
例：输入的x是32768，也就是1<<15


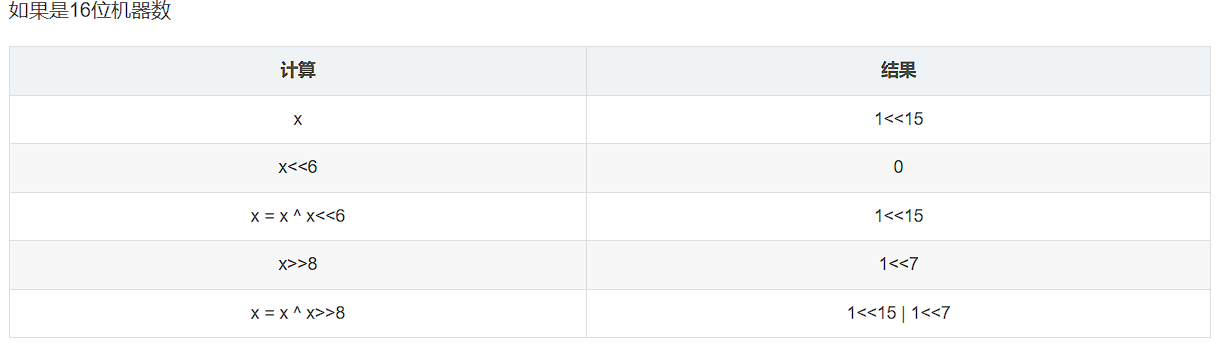
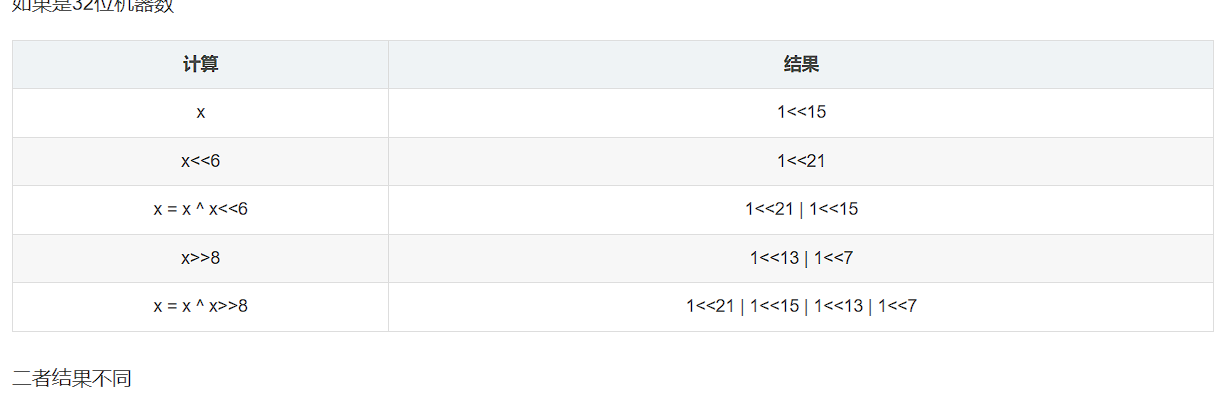
（3）

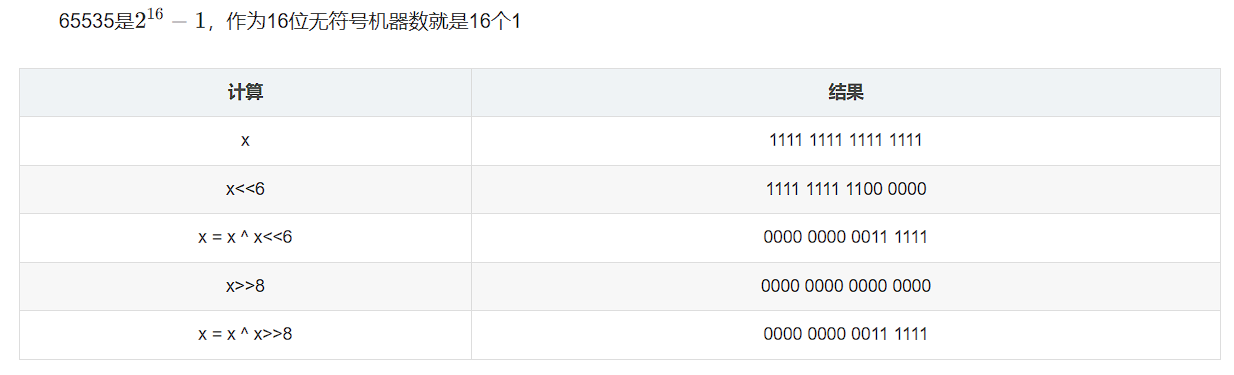
（4）

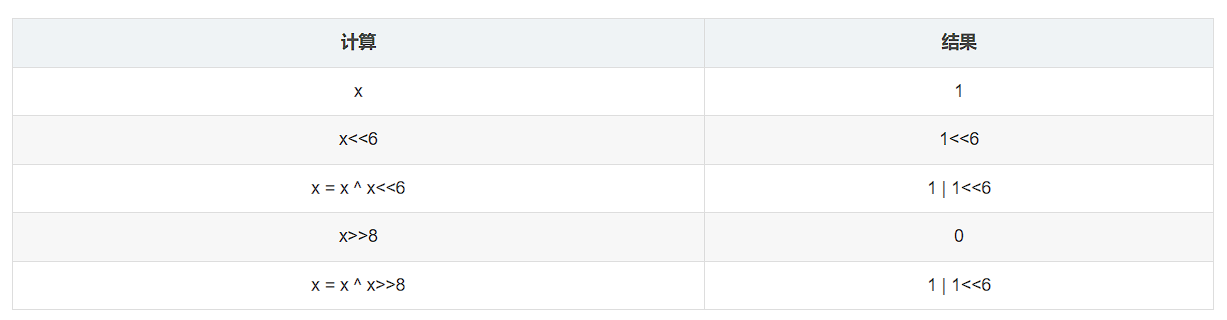
（5）

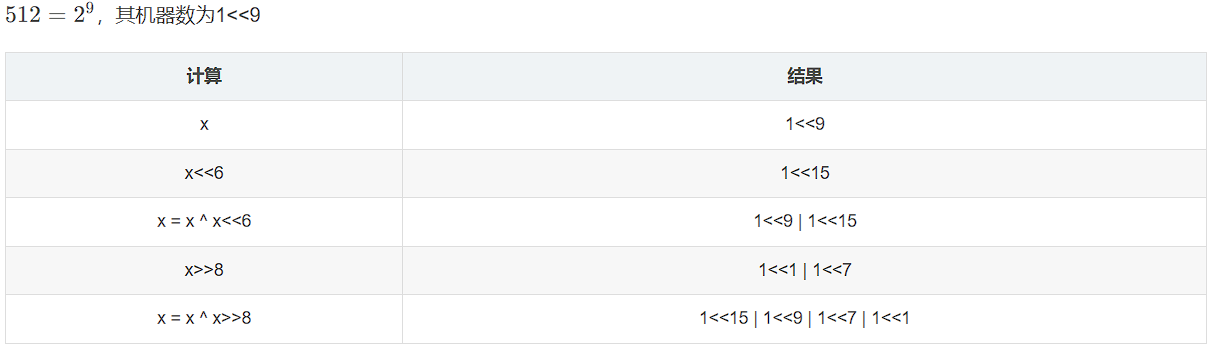
（6）

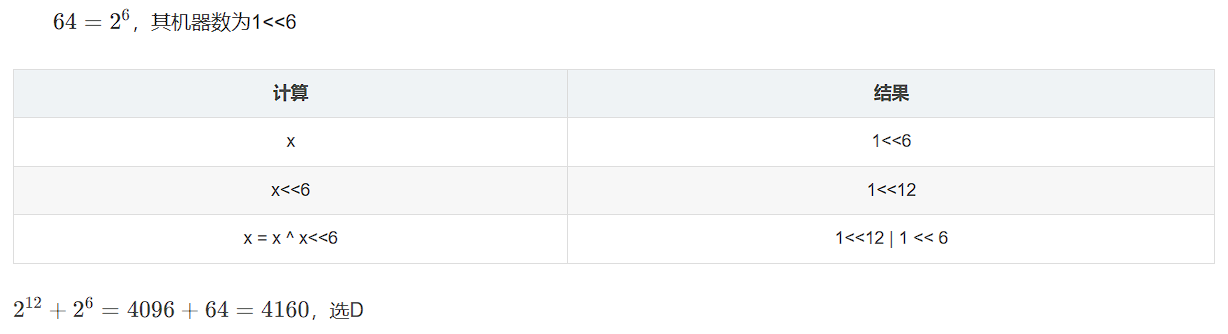
17

本题的代码是字符串匹配中的sunday算法，用于寻找t在s中出现的第一个位置，在匹配过程中，模式串发现不匹配时，算法能跳过尽可能多的字符以进行下一步的匹配，从而提高了匹配效率。
对于模式串中的每个字符 t[j]，记录它距离模式串末尾的距离 m - j。
这是 Sunday 算法的核心预处理，用于在匹配失败时决定主串的下一次比较起始位置。
遍历主串 s，尝试从位置 i 开始匹配 t。
匹配失败时，根据主串中 当前匹配窗口后一位字符 s[i + m] 的跳跃值 shift[s[i + m]] 来更新 i。
重点： s[i + m] 是主串中紧跟当前匹配窗口后的第一个字符。
（1）第一个串里不存在第二个串，因此为-1
（2）在abbababbbab中，abab第一次出现的位置应该是3，下标从0开始。
（3）正确，因为第一次2出现后的串就是20这个子串，j++两次就匹配成功了
（4）最坏复杂度可能到O(N*M)，例如这个例子 s=“aaaaaab” t=“ab”
（5）a.find(b)就是在a这个串内找b这个串第一次出现的位置。
（6）模拟即可

18

（1）输入字符0，对应的askii码是48。
48 = 0000 0000 0011 0000
1：48 << 6 = 0000 1100 0000 0000
x = 0000 0000 0011 0000
^ 0000 1100 0000 0000
= 0000 1100 0011 0000 = 3120
2：0000 1100 0011 0000 >> 5 =
0000 0000 0110 0001 ^
0000 1100 0011 0000 =
0000 1100 0101 0001 = 3153
3 ：
0000 1100 0101 0001 << 1 =
0001 1000 1010 0010 ^
0000 1100 0101 0001 =
0001 0100 1111 0011 = 5363
（2）不会变化，因为char最多八位，左移6位或者五位都不会溢出，因此short和int都一样
（3）会变化，因为char读入的是字符，传递给函数的是askii码
而换成short读入的是数字，传给函数的就是数字本身了。
（4）输入的是10，但是只会读入字符’1’，传递给x的askii码为49
49 = 0000 0000 0011 0001
0000 0000 0011 0001 << 6 =
0000 1100 0100 0000 ^
0000 0000 0011 0001 =
0000 1100 0111 0001

0000 1100 0111 0001 >> 5 =
0000 0000 0110 0011 ^
0000 1100 0111 0001 =
0000 1100 0001 0010

0000 1100 0001 0010 << 1 =
0001 1000 0010 0100 ^
0000 1100 0001 0010 =
0001 0100 0011 0110 =
5174
（5）
0000 0000 0000 1010 ^
0000 0010 1000 0000 =
0000 0010 1000 1010

0000 0010 1000 1010 ^
0000 0000 0001 0100 =
0000 0010 1001 1110

0000 0010 1001 1110 ^
0000 0101 0011 1100 =
0000 0111 1010 0010 = 1954

19

（1）pre是前一个值，cur是当前值，所以选A
（2）计算公比，当前/前一个 所以选C
（3）如果当前的值不是公比*前一个的值，那么就不是等比数列，所以选D
（4）把当前值复制到前一个值内 所以选C
（5）如果 i>n代表循环是自然退出的，没被break打断，所以选A

20

（1）原来的数字拆开存在a数组内，所以选B，传入的是地址，因此是*a
（2）转化b进制，就要x%b，x/b，类似于短除法变换2进制。
所以选A。
（3）is_pal这个函数是为了判断平方是不是回文数，因此对应的是cntaa，所以选C
（4）
B代表的是一个指针，因此不能填。
（5）
不在0到9内就是超过10进制的数字了，用大写字母‘A’代表10，依次类推，所以选D。