当前位置：首页 > news >正文

决策树算法小结（中）

news 2025/8/2 8:19:57

一、ID3算法

ID3算法就是用信息增益大小来判断当前节点应该用什么特征来构建决策树，用计算出的信息增益最大的特征来建立决策树的当前节点。这里我们举一个信息增益计算的具体的例子。

输入的是m个样本，样本输出集合为D，每个样本有n个离散特征，特征集合即为A，输出为决策树T。

算法的过程为：

初始化信息增益的阈值ϵ
判断样本是否为同一类输出Di，如果是则返回单节点树T。标记类别为Di
判断特征是否为空，如果是则返回单节点树T，标记类别为样本中输出类别D实例数最多的类别。
计算A中的各个特征（一共n个）对输出D的信息增益，选择信息增益最大的特征Ag
如果Ag的信息增益小于阈值ϵ，则返回单节点树T，标记类别为样本中输出类别D实例数最多的类别。
否则，按特征Ag的不同取值Agi将对应的样本输出D分成不同的类别Di。每个类别产生一个子节点。对应特征值为Agi。返回增加了节点的数T。
对于所有的子节点，令D=Di,A=A−{Ag}递归调用2-6步，得到子树Ti并返回。

算法不足：

ID3没有考虑连续特征，比如长度，密度都是连续值，无法在ID3运用。这大大限制了ID3的用途。
ID3采用信息增益大的特征优先建立决策树的节点。很快就被人发现，在相同条件下，取值比较多的特征比取值少的特征信息增益大。比如一个变量有2个值，各为1/2，另一个变量为3个值，各为1/3，其实他们都是完全不确定的变量，但是取3个值的比取2个值的信息增益大。如果校正这个问题呢？-信息增益比
ID3算法对于缺失值的情况没有做考虑
没有考虑过拟合的问题

例题讲解

以贷款申请样本数据集为例，初始化阈值=0.001，非空样本集。

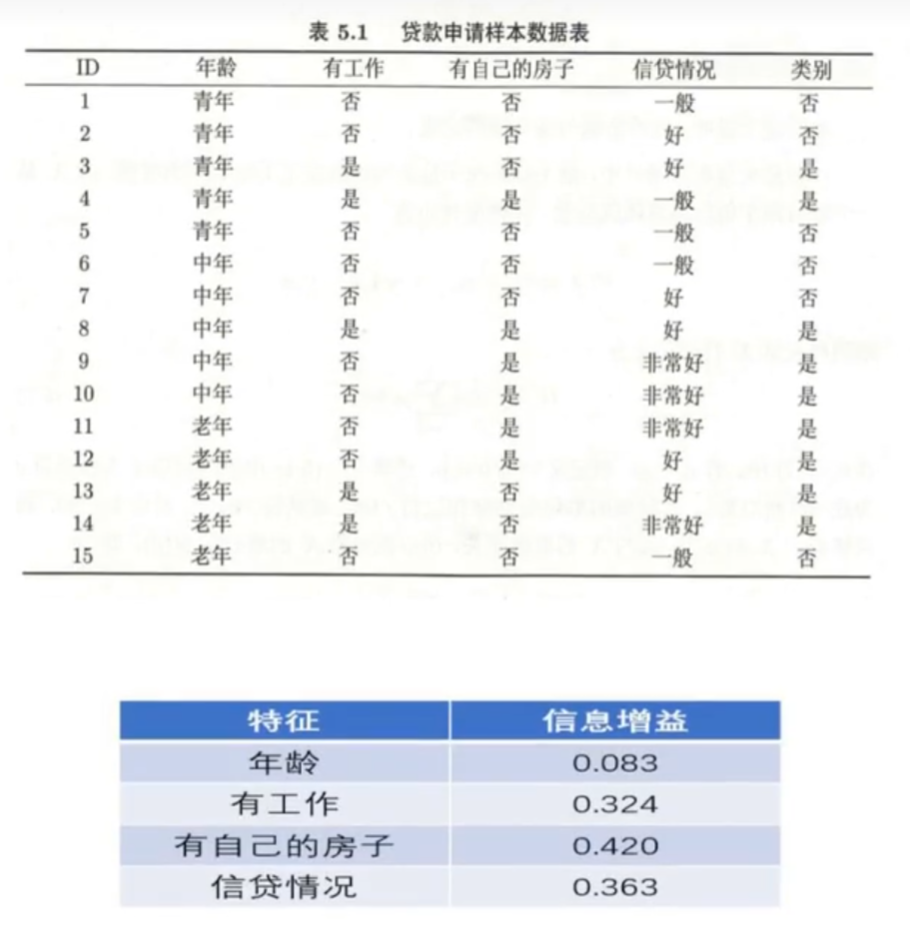
选择信息增益最大的特征有自己的房子作为根节点。

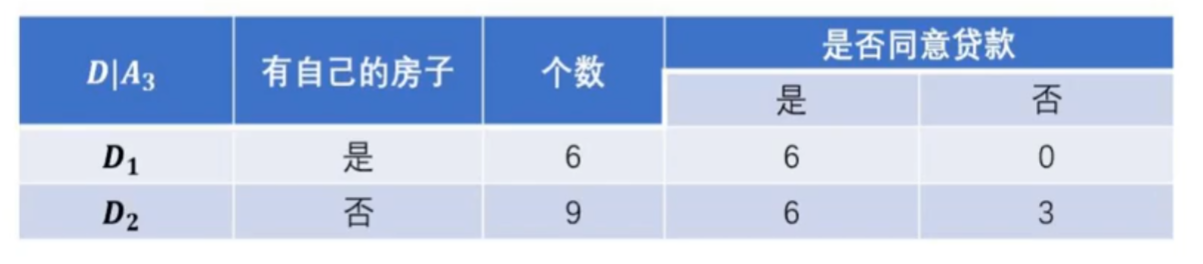
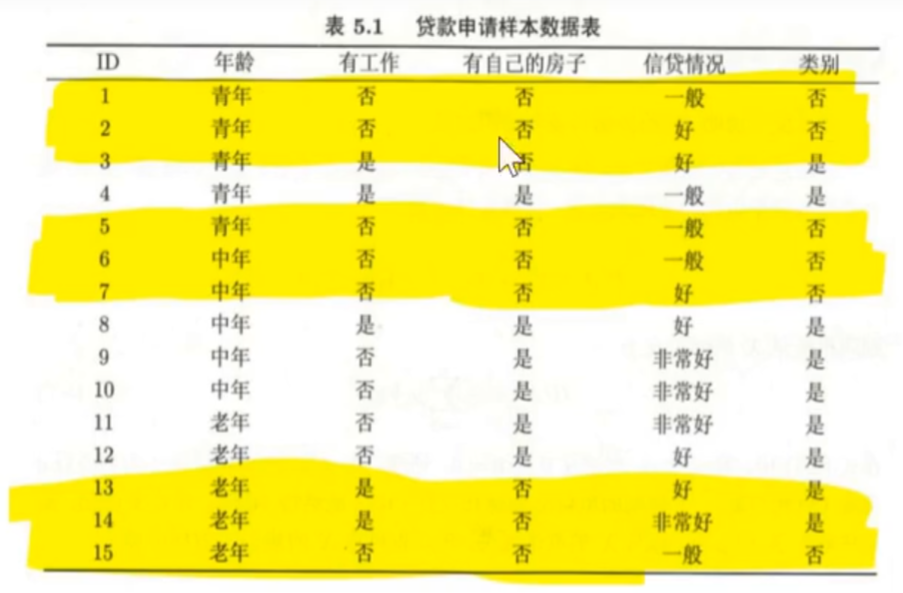
特征有自己的房子D1样本集由于全部是同意贷款，因此直接生成叶子节点。但是D2样本就需要进行特征选择，将D2作为一个新的训练数据集（A1，A2，A4作为新的特征集，来计算信息增益），新的训练数据集如下图黄色标注。

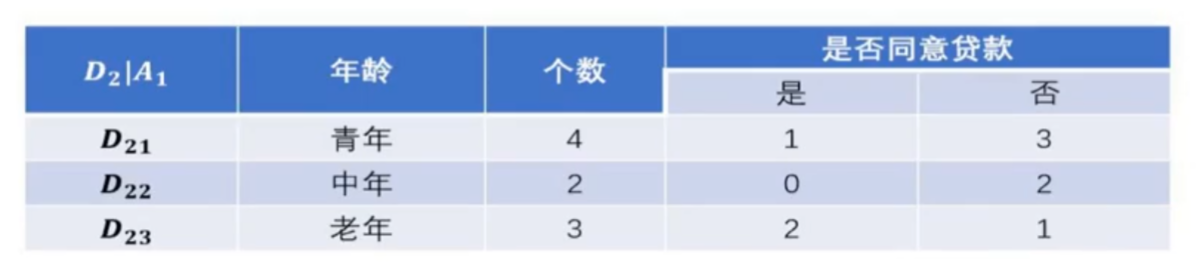
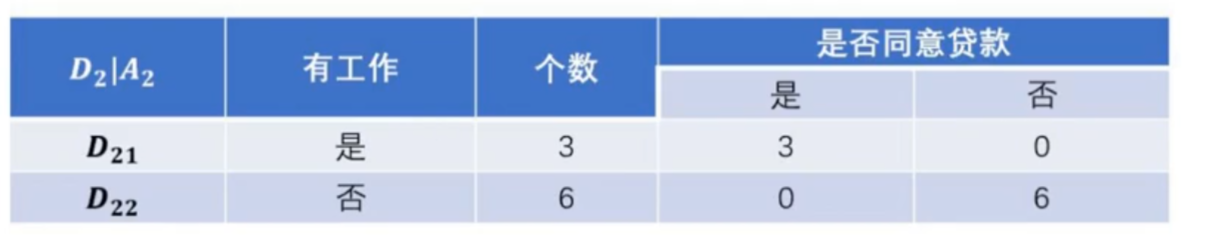
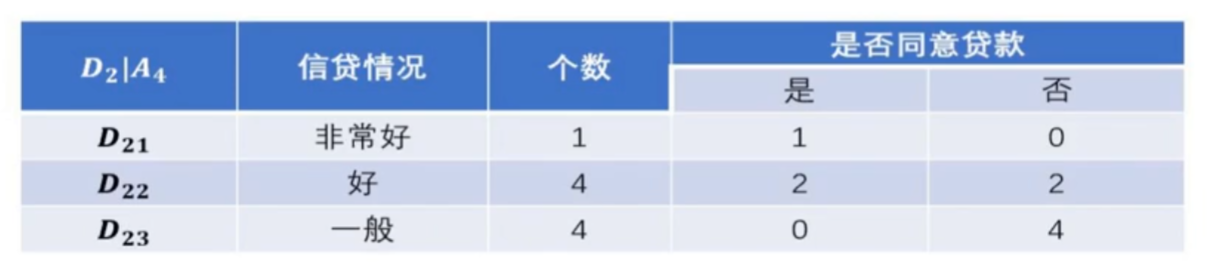
分别计算出对应的经验熵、条件经验熵、以及信息增益后如下表所示：

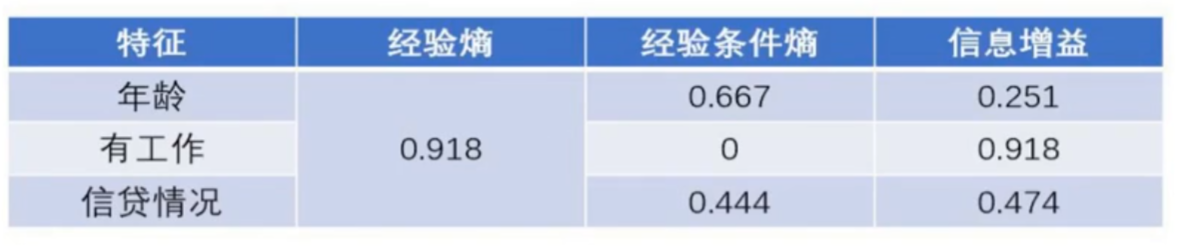
由于计算出的信息增益最大的是特征有工作的情况。因此决策树下一个节点是有工作。

因此决策树绘制如下：

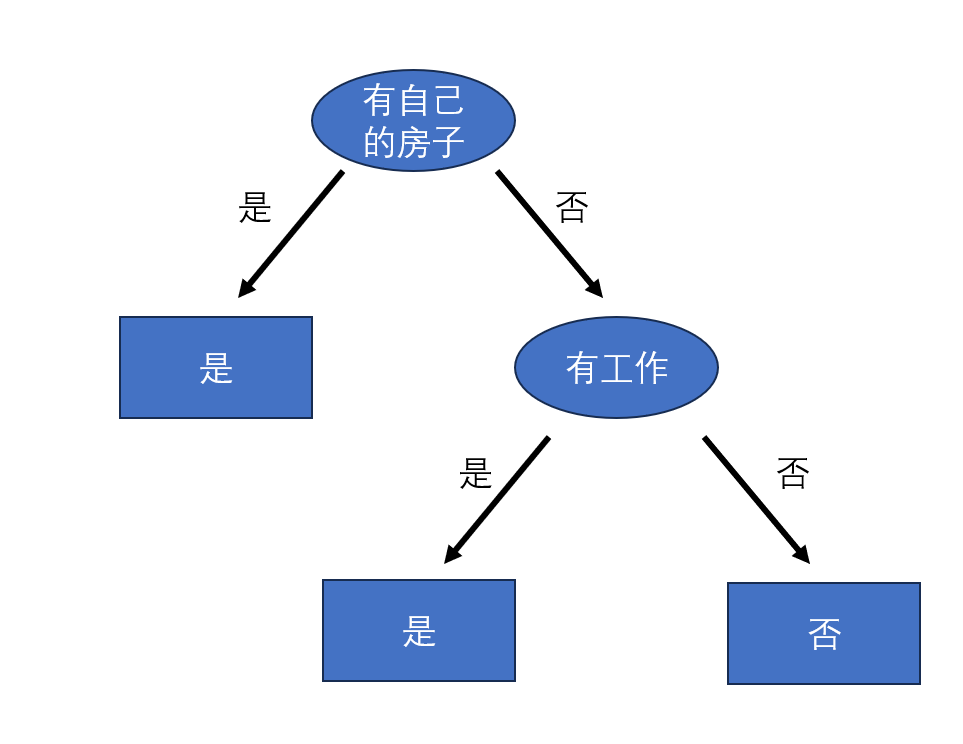
因为选择特征有工作之后，两个小子集都是属于同一类别，决策树不再继续。

二、C4.5算法

ID3算法有四个主要的不足，一是不能处理连续特征，第二个就是用信息增益作为标准容易偏向于取值较多的特征，最后两个是缺失值处理的问和过拟合问题。

对于第一个问题，不能处理连续特征， C4.5的思路是将连续的特征离散化。比如m个样本的连续特征A有m个，从小到大排列为 $a_{1},a_{2},...,a_{m}$ ，则C4.5取相邻两样本值的平均数，一共取得m-1个划分点，其中第i个划分点 $T_{i}$ 表示为： $\frac{a_{i}+a_{i+1}}{2}$ 。对于这m-1个点，分别计算以该点作为二元分类点时的信息增益。选择信息增益最大的点作为该连续特征的二元离散分类点。比如取到的增益最大的点为 $a_{t}$ ，则小于 $a_{t}$ 的值为类别1，大于 $a_{t}$ 的值为类别2，这样就做到了连续特征的离散化。
对于第二个问题，信息增益作为标准容易偏向于取值较多的特征的问题。引入信息增益比的变量，它是信息增益和特征熵的比值。特征数越多的特征对应的特征熵越大，它作为分母，可以校正信息增益容易偏向于取值较多的特征的问题。
对于第三个缺失值处理的问题，主要需要解决的是两个问题，一是在样本某些特征缺失的情况下选择划分的属性，二是选定了划分属性，对于在该属性上缺失特征的样本的处理。
1. 对于第一个子问题，对于某一个有缺失特征值的特征A。C4.5的思路是将数据分成两部分，对每个样本设置一个权重（初始可以都为1），然后划分数据，一部分是有特征值A的数据D1，另一部分是没有特征A的数据D2. 然后对于没有缺失特征A的数据集D1来和对应的A特征的各个特征值一起计算加权重后的信息增益比，最后乘上一个系数，这个系数是无特征A缺失的样本加权后所占加权总样本的比例。
2. 对于第二个子问题，可以将缺失特征的样本同时划分入所有的子节点，不过将该样本的权重按各个子节点样本的数量比例来分配。比如缺失特征A的样本a之前权重为1，特征A有3个特征值A1,A2,A3。 3个特征值对应的无缺失A特征的样本个数为2,3,4.则a同时划分入A1，A2，A3。对应权重调节为2/9,3/9, 4/9。
对于第4个问题，C4.5引入了正则化系数进行初步的剪枝。

算法不足：

由于决策树算法非常容易过拟合，因此对于生成的决策树必须要进行剪枝。
C4.5生成的是多叉树，即一个父节点可以有多个节点，效率不高。
C4.5只能用于分类，如果能将决策树用于回归的话可以扩大它的使用范围。
C4.5由于使用了熵模型，里面有大量的耗时的对数运算，如果是连续值还有大量的排序运算，运算强度大。

学习链接：

决策树算法原理(上) - 刘建平Pinard - 博客园https://www.cnblogs.com/pinard/p/6050306.html5.4 决策树的生成——例题详解_哔哩哔哩_bilibilihttps://www.bilibili.com/video/BV1No4y1o7ac?spm_id_from=333.788.videopod.episodes&vd_source=90c4af5a77af61e3c51cdb5f018cca32&p=40