Deep Learning_ Foundations and Concepts-Springer (2024)【拜读】前向编码器20章

Diffusion Models 扩散模型
我们已经了解到,构建强大的生成模型的一种有效方法是:先引入一个关于潜在变量z的分布p(z),然后使用深度神经网络将z变换到数据空间x。由于神经网络具有通用性,能够将简单固定的分布转化为关于x的高度灵活的分布族,因此为p(z)采用如高斯分布N(z|0, I)这类简单固定的分布就足够了。在之前的章节中,我们探讨了多种符合这一框架的模型,这些模型基于生成对抗网络、变分自编码器以及归一化流,在定义和训练深度神经网络方面采用了不同的方法。
在本章中,我们将探讨这一通用框架下的第四类模型,即扩散模型(diffusion models),也被称为去噪扩散概率模型(denoising diffusion probabilistic models,简称DDPMs)(Sohl-Dickstein等人,2015年;Ho、Jain和Abbeel,2020年)。这类模型已成为许多应用领域中最先进的模型。为便于说明,我们将重点讨论图像数据模型,尽管该框架具有更广泛的适用性。其核心思想是,对每张训练图像应用多步加噪过程,将其逐步破坏并最终转化为一个服从高斯分布的样本。这一过程如图20.1所示。随后,训练一个深度神经网络来逆转这一过程;一旦训练完成,该网络就可以从高斯分布中采样作为输入,进而生成新的图像。
扩散模型可被视为一种分层变分自编码器的变体,其中编码器分布是固定的,由加噪过程所定义,而仅需学习生成分布(Luo,2022)。这类模型易于训练,在并行硬件上扩展性良好,且能规避对抗训练中的挑战与不稳定性问题,同时生成结果的质量可与生成对抗网络相媲美甚至更优。然而,由于需要通过解码器网络进行多次前向传播,生成新样本的计算成本可能较高(Dhariwal和Nichol,2021)。
20.1 Forward Encoder 前向编码器
假设我们从训练集中选取一张图像,记为 x,然后对每个像素独立地添加高斯噪声进行混合,得到一个受噪声干扰的图像 z₁,其定义如下:
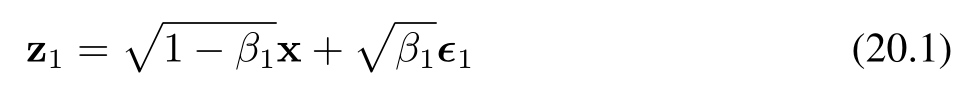
其中,ε₁ ∼ N(ε₁|0, I),且 β₁ < 1 为噪声分布的方差,β₁ ∈ (0,1):控制噪声强度的超参数(称为噪声的方差系数)。公式(20.1)和(20.3)中系数 √(1 − β₁) 和 √β₁ 的选取,确保了 zₜ 的分布均值相较于 zₜ₋₁ 更接近零,且 zₜ 的协方差矩阵相较于 zₜ₋₁ 更接近单位矩阵。我们可以将变换(20.1)改写为如下形式:
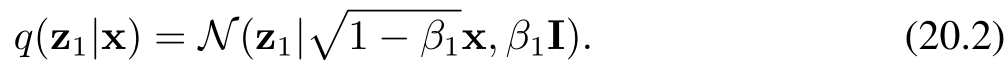
随后,我们通过多次添加独立的加性高斯噪声,重复这一过程,从而生成一系列噪声逐步增强的图像序列 z₂, …, zₜ。需要注意的是,在扩散模型的相关文献中,这些潜在变量有时被记为 x₁, …, xₜ,而观测变量则记为 x₀。为与本书其余部分保持一致,我们采用 z 表示潜在变量、x 表示观测变量的符号体系。每一幅后续图像的生成方式如下:
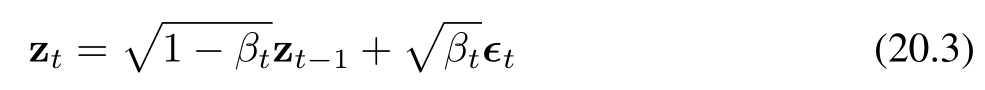
其中,εₜ ∼ N(εₜ|0, I)。同样地,我们可以将公式(20.3)改写为如下形式:
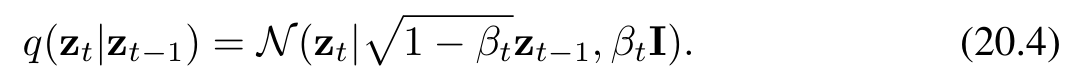
条件分布序列(20.4)构成一个马尔可夫链,并可用如图20.2所示的概率图模型表示。方差参数 βₜ ∈ (0, 1) 需手动设定,通常按照预设的递增规则选择,使得方差值沿链逐步增大,即满足 β₁ < β₂ < … < βₜ。
这个公式描述的是扩散模型(Diffusion Model)中的前向过程(Forward Process),即如何逐步向原始图像添加噪声,最终将其转化为纯噪声。详细解析公式和方差参数空间门
公式 (20.3)
zt=1−βtzt−1+βtϵtz_t = \sqrt{1 - \beta_t} z_{t-1} + \sqrt{\beta_t} \epsilon_tzt=1−βtzt−1+βtϵt
- ztz_tzt 和 zt−1z_{t-1}zt−1:分别表示在时间步 ttt 和 t−1t-1t−1 的图像(或潜在变量)。
- βt\beta_tβt:是一个预先设定的参数,取值范围在 (0,1)(0, 1)(0,1) 之间,控制每一步添加噪声的比例。
- ϵt\epsilon_tϵt:是从标准正态分布 N(ϵt∣0,I)\mathcal{N}(\epsilon_t | 0, \mathbf{I})N(ϵt∣0,I) 中采样得到的高斯噪声,其中 I\mathbf{I}I 是单位矩阵。
这个公式的含义是,在每一步 ttt,当前的图像 ztz_tzt 是由前一步的图像 zt−1z_{t-1}zt−1 加上一定比例的高斯噪声 βtϵt\sqrt{\beta_t} \epsilon_tβtϵt 得到的,同时保留了前一步图像的一部分 1−βtzt−1\sqrt{1 - \beta_t} z_{t-1}1−βtzt−1。
公式 (20.4)
q(zt∣zt−1)=N(zt∣1−βtzt−1,βtI)q(z_t | z_{t-1}) = \mathcal{N}(z_t | \sqrt{1 - \beta_t} z_{t-1}, \beta_t \mathbf{I})q(zt∣zt−1)=N(zt∣1−βtzt−1,βtI)
这个公式是从概率的角度描述了公式 (20.3)。它表示在给定 zt−1z_{t-1}zt−1 的条件下,ztz_tzt 的条件概率分布是一个均值为 1−βtzt−1\sqrt{1 - \beta_t} z_{t-1}1−βtzt−1,协方差矩阵为 βtI\beta_t \mathbf{I}βtI 的高斯分布。
参数 βt\beta_tβt 的设定
参数 βt\beta_tβt 是手动设定的,并且通常按照一个预设的递增规则选择,使得 β1<β2<⋯<βT\beta_1 < \beta_2 < \cdots < \beta_Tβ1<β2<⋯<βT。这意味着随着时间步 ttt 的增加,添加的噪声比例逐渐增大,最终在 t=Tt = Tt=T 时,图像几乎完全转化为噪声。
通过这种方式,扩散模型的前向过程逐步将原始图像转化为一个各向同性的高斯分布,为后续的逆向生成过程(即从噪声中恢复图像)奠定了基础。
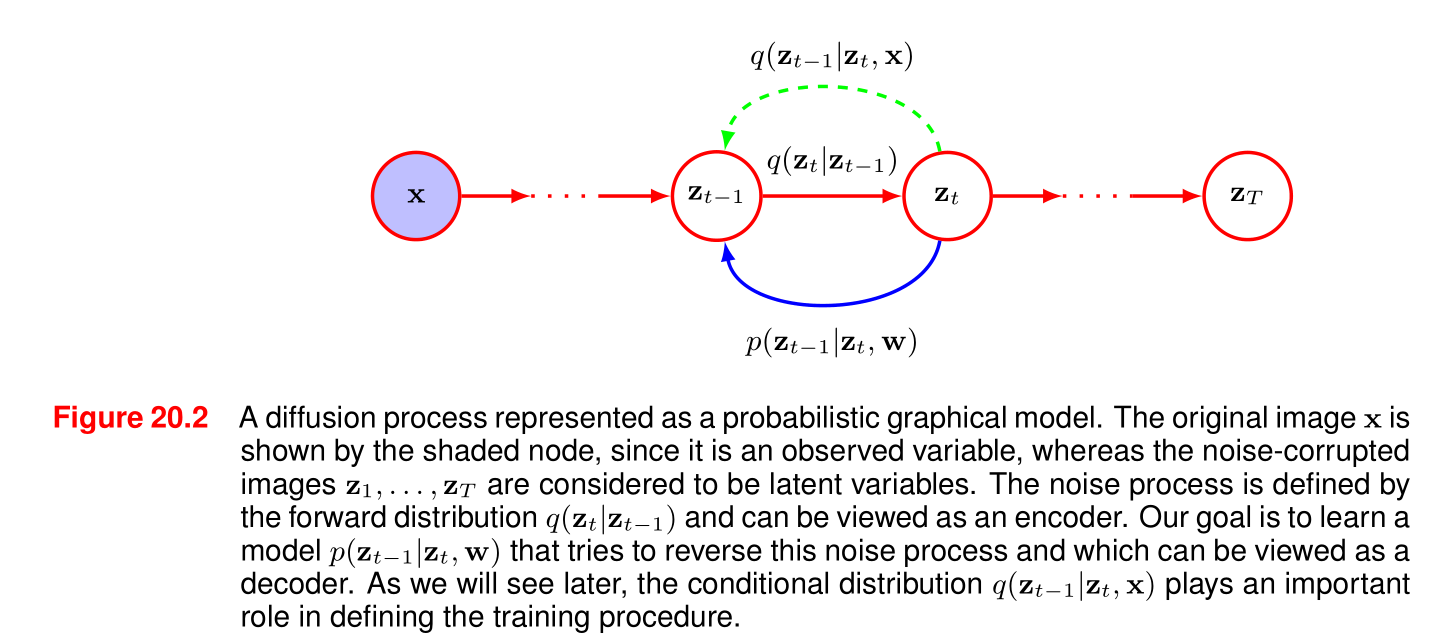
图20.2 一个表示为概率图模型的扩散过程。原始图像x\mathbf{x}x由阴影节点表示,因为它是一个观测变量,而受噪声干扰的图像z1,…,zTz_1, \ldots, z_Tz1,…,zT被视为潜在变量。噪声过程由前向分布q(zt∣zt−1)q(z_t|z_{t - 1})q(zt∣zt−1)定义,可被视为一个编码器。我们的目标是学习一个模型p(zt−1∣zt,w)p(z_{t - 1}|z_t, \mathbf{w})p(zt−1∣zt,w),该模型试图逆转这个噪声过程,可被视为一个解码器。正如我们稍后将看到的,条件分布q(zt−1∣zt,x)q(z_{t - 1}|z_t, \mathbf{x})q(zt−1∣zt,x)在定义训练过程中起着重要作用。
图的解析
这张图展示了一个用概率图模型表示的扩散过程。
-
节点和变量:
- 图中左侧的蓝色阴影节点表示原始图像 x\mathbf{x}x,它是一个观测变量。
- 红色节点 z1,…,zTz_1, \ldots, z_Tz1,…,zT 表示受噪声干扰的图像,被视为潜在变量。
-
过程描述:
- 前向过程(噪声添加过程):由前向分布 q(zt∣zt−1)q(z_t | z_{t - 1})q(zt∣zt−1) 定义,可以看作是一个编码器。从原始图像 x\mathbf{x}x 开始,通过一系列步骤逐步添加噪声,最终在 TTT 步后得到一个接近纯噪声的潜在变量 zTz_TzT。图中绿色虚线箭头表示了这一前向过程的方向,即从 zt−1z_{t-1}zt−1 到 ztz_tzt 的噪声添加步骤。
- 逆向过程(生成过程):目标是学习一个模型 p(zt−1∣zt,w)p(z_{t - 1} | z_t, \mathbf{w})p(zt−1∣zt,w),试图逆转这个噪声添加过程,可以看作是一个解码器。图中蓝色实线箭头表示了逆向过程的方向,即从 ztz_tzt 恢复到 zt−1z_{t - 1}zt−1 的步骤。
-
条件分布的作用:
- 条件分布 q(zt−1∣zt,x)q(z_{t - 1} | z_t, \mathbf{x})q(zt−1∣zt,x) 在定义训练过程中起着重要作用。它结合了观测变量 x\mathbf{x}x 的信息,帮助模型学习如何从噪声潜在变量 ztz_tzt 恢复到前一步的潜在变量 zt−1z_{t - 1}zt−1。
总体而言,这张图直观地展示了扩散模型中前向的噪声添加过程和逆向的生成过程,以及各个变量和分布之间的关系。
20.1.1 Diffusion kernel
在给定观测数据向量 x\mathbf{x}x 的条件下,潜在变量的联合分布由下式给出: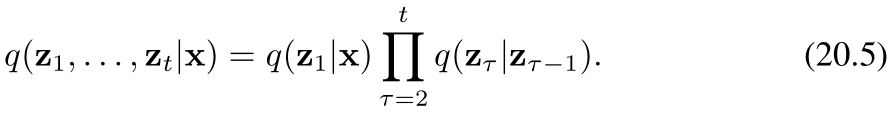
如果我们现在对中间变量 z1,…,zt−1z_1, \ldots, z_{t - 1}z1,…,zt−1 进行边缘化处理(边缘化处理的目的是消除中间变量,从而得到仅关于 ztz_tzt 和 x\mathbf{x}x 的条件概率分布 q(zt∣x)q(\mathbf{z}_t | \mathbf{x})q(zt∣x)),就得到了扩散核:
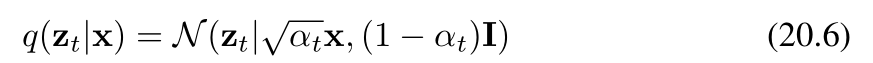
在此我们定义:

我们看到,每个中间分布都有一个简单的闭式高斯表达式,我们可以直接从中进行采样。这在训练去噪扩散概率模型(Denoising Diffusion Probabilistic Models, DDPMs)时将被证明是很有用的,因为它允许使用马尔可夫链中随机选择的中间项来进行高效的随机梯度下降,而无需运行整个链。我们还可以将公式(20.6)写成如下形式
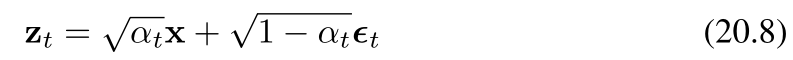
其中再次(有)ϵt∼N(ϵt∣0,I)\epsilon_t \sim \mathcal{N}(\epsilon_t|0, \mathbf{I})ϵt∼N(ϵt∣0,I)(这里表示ϵt\epsilon_tϵt服从均值为0、协方差矩阵为单位矩阵I\mathbf{I}I的多元正态分布)。请注意,此时ϵt\epsilon_tϵt代表添加到原始图像上的总噪声,而不是在马尔可夫链的这一步添加的增量噪声。
经过许多步骤后,图像变得与高斯噪声无法区分,当步数 TTT 趋于无穷大(T→∞T \to \inftyT→∞)时,我们有(以下情况/结果)

因此,关于原始图像的所有信息都丢失了。公式 (20.3) 中系数 1−βt\sqrt{1 - \beta_t}1−βt 和 βt\sqrt{\beta_t}βt 的选择确保了一旦马尔可夫链收敛到一个均值为0、协方差为单位矩阵的分布,进一步的更新将不会改变这一分布。
由于公式 (20.9) 的右侧与 x\mathbf{x}x(或 x,根据上下文确定具体变量)无关,因此可以得出 zTz_TzT(或 zT\mathbf{z}_TzT ,根据上下文确定具体变量)的边缘分布由以下式子给出(或可表示为)

人们通常将马尔可夫链(公式20.4)称为前向过程,它类似于变分自动编码器(VAE)中的编码器,只不过这里(马尔可夫链所代表的过程)是固定的,而非通过学习得到的。然而,需要注意的是,文献中的常用术语与标准化流(normalizing flows)相关文献中通常使用的术语是相反的,在标准化流的文献中,从潜在空间到数据空间的映射被视为前向过程。
20.1.2 Conditional distribution 条件扩散
我们的目标是学会逆转(消除、还原)加噪过程,因此很自然地会考虑条件分布 q(zt∣zt−1)q(z_t | z_{t - 1})q(zt∣zt−1) 的逆过程,我们可以借助贝叶斯定理将其表示为如下形式
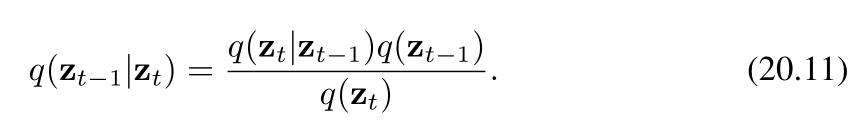
我们可以将边缘分布 q(zt−1)q(z_{t-1})q(zt−1) 表示为如下形式
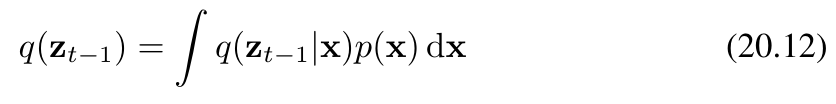
其中,q(zt−1∣x)q(z_{t-1}|\mathbf{x})q(zt−1∣x) 由条件高斯分布(公式20.6)给出。然而,该分布难以直接处理(无法解析求解),因为我们必须对未知的数据分布 p(x)p(\mathbf{x})p(x) 进行积分。如果我们使用训练数据集中的样本对积分进行近似,则会得到一个复杂的分布,该分布可表示为高斯混合分布。
相反,我们考虑反向分布的条件版本,即在给定数据向量 x\mathbf{x}x 的条件下,定义为 q(zt−1∣zt,x)q(z_{t-1}|z_t, \mathbf{x})q(zt−1∣zt,x) 的分布。我们很快将会看到,该分布实际上是一个简单的高斯分布。从直觉上看,这是合理的:因为给定一张含噪图像时,很难推测出是哪张低噪声图像生成了它;而如果我们还知道原始(起始)图像,那么问题就会变得简单得多。我们可以利用贝叶斯定理来计算这个条件分布:
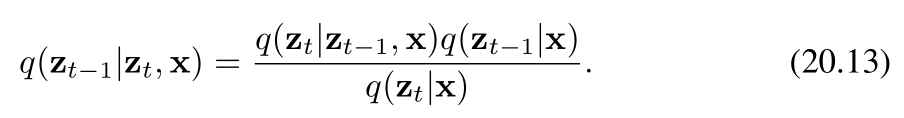
现在,我们利用前向过程的马尔可夫性质来进行推导(ztz_tzt只和前一时刻zt−1z{t-1}zt−1有关,与x无关)
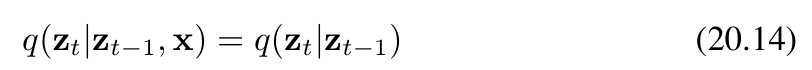
其中,等式右侧由(20.4)式给出。作为 zt−1z_{t-1}zt−1 的函数,它呈现为二次型的指数形式。(20.13)式分子中的 q(zt−1∣x)q(z_{t-1}|\mathbf{x})q(zt−1∣x) 项是由(20.6)式给出的扩散核,它同样涉及关于 zt−1z_{t-1}zt−1 的二次型指数。由于(20.13)式的分母作为 zt−1z_{t-1}zt−1 的函数是常数,我们可以忽略它。因此,我们看到(20.13)式的右侧呈现为高斯分布的形式,并且我们可以使用“配方法”来确定其均值和协方差,具体如下:
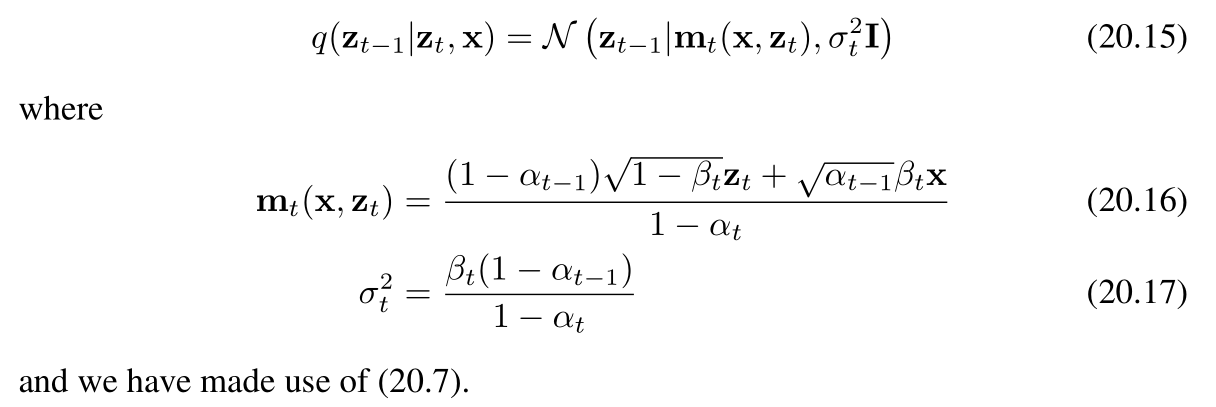
上述条件分布的转化,化简解释秘籍——》宝典
