当前位置：首页 > news >正文

力扣1457. 二叉树中的伪回文路径

news 2025/7/29 5:27:44

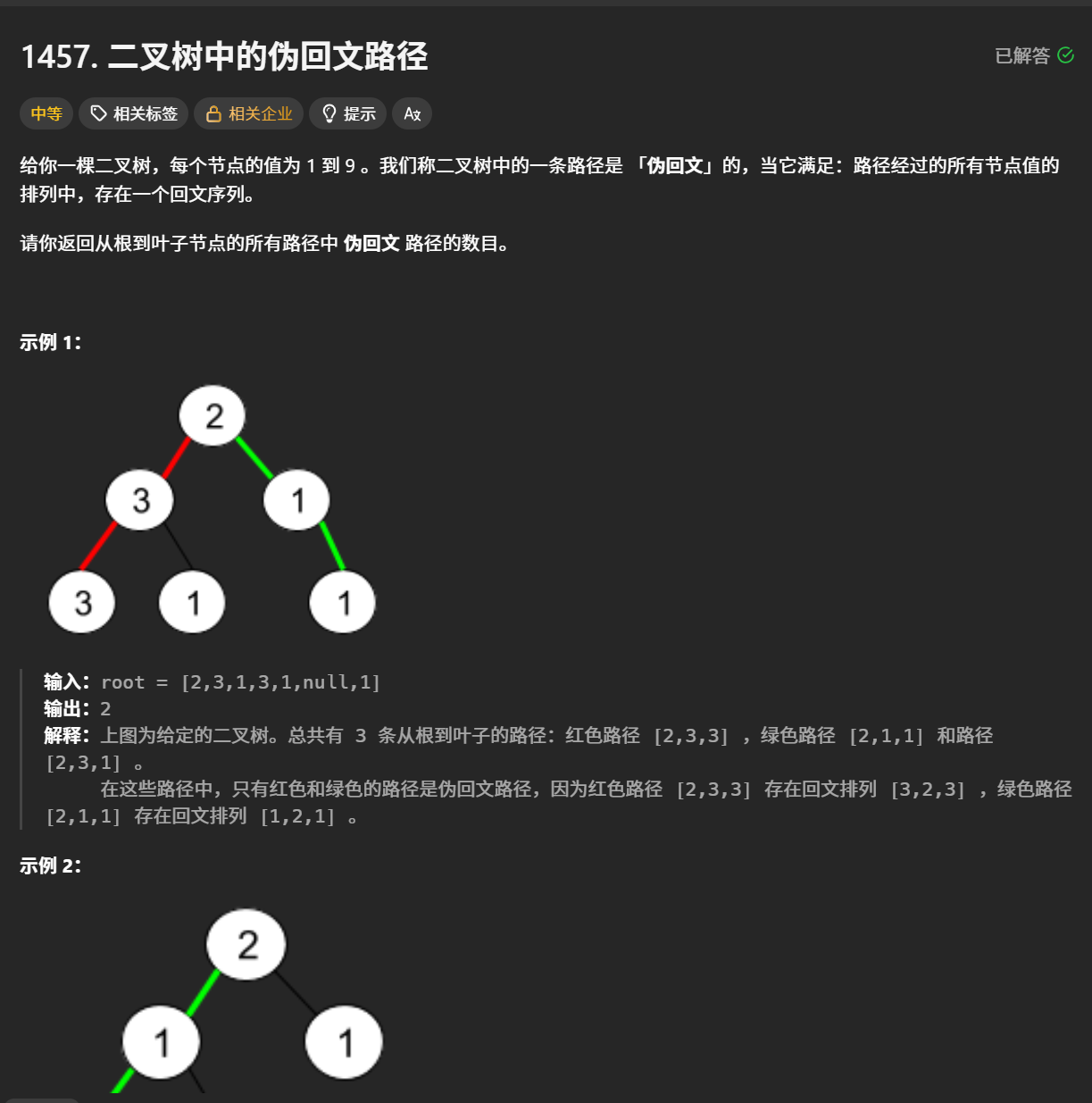
在这里插入图片描述

这一题就是正常的dfs，在遍历的过程中把所有的从根到叶子节点给放进数组里，然后判断它是不是一个伪回文串，如果是则ans++，
那么如何判断是不是一个伪回文串，回文串是具有奇偶性质的，之前的题目也遇到过
，我们可以分奇偶，奇数个的回文串我们只需要保证最多有一个数字出现奇数次，偶数个回文串，我们需要保证每一个数字都出现偶数次即可。
带着这样的思路我开始了写代码。

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<int> cnt;int ans;unordered_map<int,int> mp;// unordered_map<int,int> mp;bool ishuiwen(vector<int>& cnt){if(cnt.size()==1){return true;}else{if(cnt.size()%2==0){mp.clear();for(int i=0;i<cnt.size();i++){mp[cnt[i]]++;}for(auto it: mp){if(it.second%2==0){}else{return false;}}return true;}else{mp.clear();for(int i=0;i<cnt.size();i++){mp[cnt[i]]++;}int flag=0;for(auto it: mp){if(it.second%2==0){}else {if(flag==1){return false;}else{flag++;}}}return true;}}}void dfs(TreeNode* root,vector<int>&cnt){if(root==nullptr){return ;}else{cnt.push_back(root->val);if(root->left==nullptr&&root->right==nullptr){//说明构成了一个序列了，我们只需要判断它是不是回文序列//判断一个序列是不是回文序列  if(ishuiwen(cnt)){ans++;}cnt.pop_back();return;                   }// cnt.push_back(root->val);dfs(root->left,cnt);dfs(root->right,cnt);cnt.pop_back(); }}int pseudoPalindromicPaths (TreeNode* root) {if(root==nullptr){return 0;}dfs(root,cnt);return ans;}
};

在获得一个伪回文串后，就用哈希表保存它中的所有元素，然后再按照上面我提到的判断方法判断，可以得到正确答案，**我们要注意访问过的序列，在dfs回溯的过程中也需要让它弹出序列。**我的这种思路虽然是对的，但是时间复杂度太高了，因为我是在得到序列后再放入哈希表，再判断，dfs得到序列的过程就已经O（n），后面在放哈希表再判断就O（n^2)根据数据范围，是超出时间限制的。
因此，我们应该在dfs访问和回溯的过程中，放入哈希表，当得到序列的时候，直接判断是不是回文串就可以。

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<int> cnt;int ans;int f[10];void dfs(TreeNode* root,vector<int>&cnt){if(root==nullptr){return ;}else{cnt.push_back(root->val);f[root->val]++;if(root->left==nullptr&&root->right==nullptr){if(cnt.size()==1){ans++;}else{if(cnt.size()%2==0){bool isflag=0;for(int i=1;i<=9;i++){if(f[i]%2==0){}else{isflag=1;}}if(isflag==0){ans++;}}else{int flag=0;for(int i=1;i<=9;i++){if(f[i]%2==0){}else{flag++;}}if(flag<=1){ans++;}}}//说明构成了一个序列了，我们只需要判断它是不是回文序列cnt.pop_back(); f[root->val]--;return ;}dfs(root->left,cnt); dfs(root->right,cnt);cnt.pop_back(); f[root->val]--;}}int pseudoPalindromicPaths (TreeNode* root) {if(root==nullptr){return 0;}dfs(root,cnt);return ans;}
};
···
我这里的vector<int> cnt，实际上是多余了，可以去掉的。
**注意理解回溯和递归是解决这一题的关键。**
时间复杂度O(n),因为根据题目上的数据范围，判断回文串是常数级