【数据结构】二叉树初阶详解(二):实现逻辑与代码拆解(超详版)
文章目录
- 🌄前言
- 🌄头文件(函数的声明)
- 🌄源文件(函数的定义)详解
- 🌆创建树的新结点
- 🌆二叉树前序遍历
- 🌆二叉树中序遍历
- 🌆二叉树后序遍历
- 🌆二叉树的层序遍历
- 🌆二叉树节点个数
- 🌆二叉树叶子节点个数
- 🌆二叉树第k层节点个数
- 🌆二叉树查找值为x的节点
- 🌆判断二叉树是否是完全二叉树
- 🌆二叉树销毁
- 🌆通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
- 🌄完整代码实现
- 🌆Queue.h文件
- 🌆Queue.c文件
- 🌆BinaryTree.h文件
- 🌆BinaryTree.c文件
- 🌆test.c文件
- ❤️总结
🌄前言
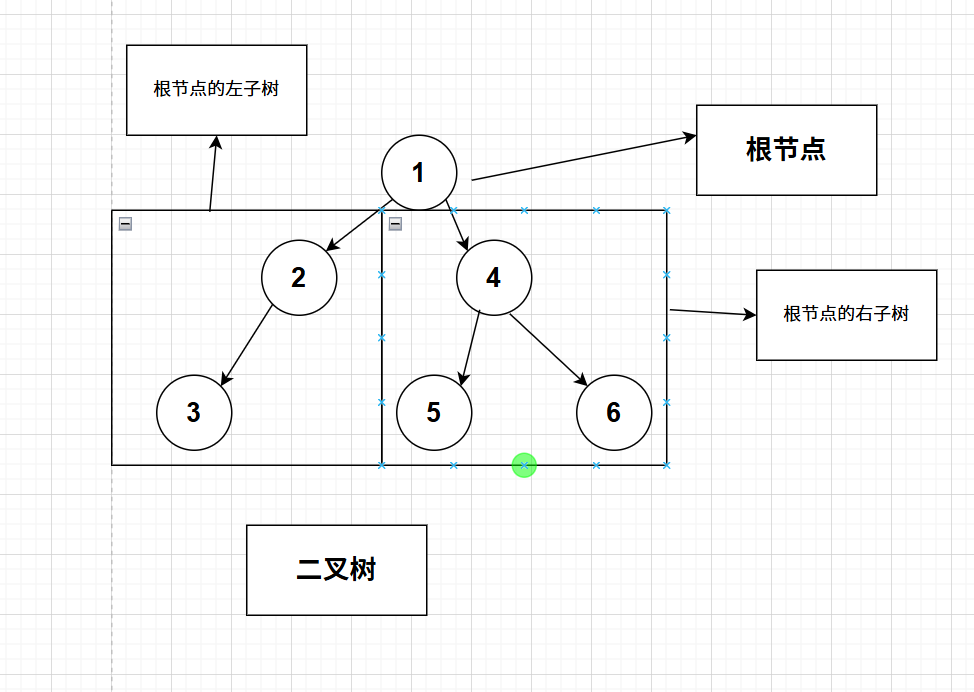
再二叉树基本操作前,回顾下二叉树的概念,二叉树是:
- 空树
- 非空:根节点,根节点的左子树、根节点的右子树组成的。
从概念中可以看出,二叉树定义是递归式的,因此后序基本操作中基本都是按照该概念实现的。
🌄头文件(函数的声明)
#pragma once#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#include<assert.h>
typedef int BTDataType;
typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;
//创建一个新结点
BTNode* BuyNode(BTDataType x);
// 二叉树前序遍历
void PreOrder(BTNode* root);
// 二叉树中序遍历
void InOrder(BTNode* root);
// 二叉树后序遍历
void PostOrder(BTNode* root);
// 层序遍历
void LevelOrder(BTNode* root);
// 二叉树节点个数
int BinaryTreeSize(BTNode* root);
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root);
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k);
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);
// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi);
// 二叉树销毁
void BinaryTreeDestory(BTNode* root);
// 判断二叉树是否是完全二叉树
bool BinaryTreeComplete(BTNode* root);🌄源文件(函数的定义)详解
🌆创建树的新结点
BTNode* BuyNode(BTDataType x)
{BTNode* node = (BTNode*)malloc(sizeof(BTNode));if (node == NULL){perror("malloc fail");return NULL;}node->data = x;node->left = NULL;node->right = NULL;return node;
}
函数解释:
1.用 malloc 分配 BTNode 大小的内存给 node 指针。
2.检查内存分配是否失败,失败则打印错误并返回 NULL 。
3.给节点 data 赋值为传入的 x,并将 left、right 子指针初始化为 NULL 。
4.返回创建好的节点指针,用于构建二叉树。
🌆二叉树前序遍历
// 二叉树前序遍历
void PreOrder(BTNode* root)
{if(root==NULL){printf("NULL");return;}printf("%d",root->data);PreOrder(root->left);preOrder(root->right);
}
对于前序遍历,我的理解是它通过将根节点的指针传入,在将其指针判断是否为空,紧接着打印根节点的数据,在通过递归访问根节点的左子树,再访问根结点的右子树。并且通过这个递归,我们可以又将根结点的子树再看作根节点,这样就能先访问根结点的左子树,如果见底,再返回访问右子树。所以他又可以是根左右这种叫法。
举个例子:
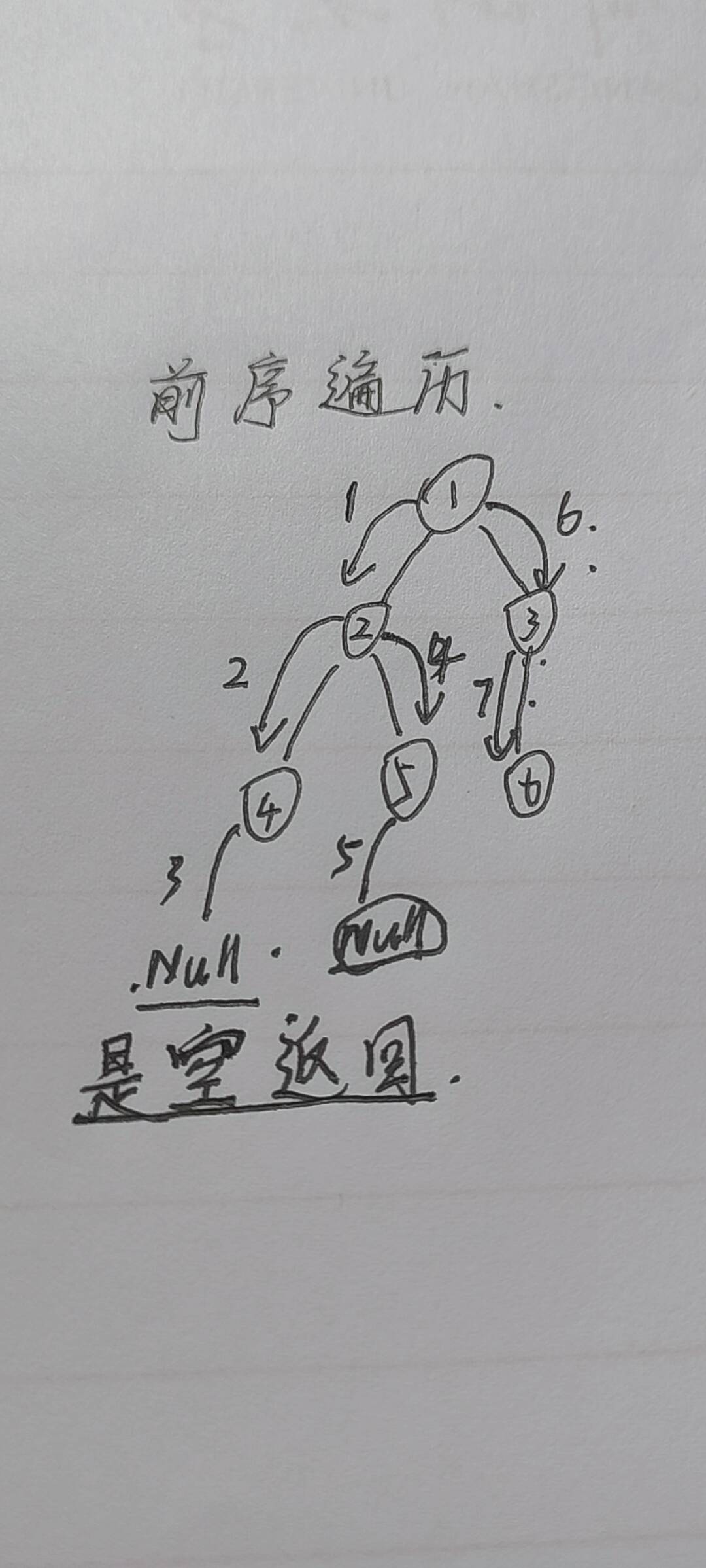
简单来说就是从根往左走到底,再回到右边再从左走,边里的结果是1 2 4 5 3 6.
🌆二叉树中序遍历
// 二叉树中序遍历
void InOrder(BTNode* root)
{if(root == NULL){printf("NULL");return;}InOrder(root->left);printf("%d",root->data);InOrder(root->right);
}
对于中序遍历,按照前面的前序遍历的理解,它可以是左根右
举个例子
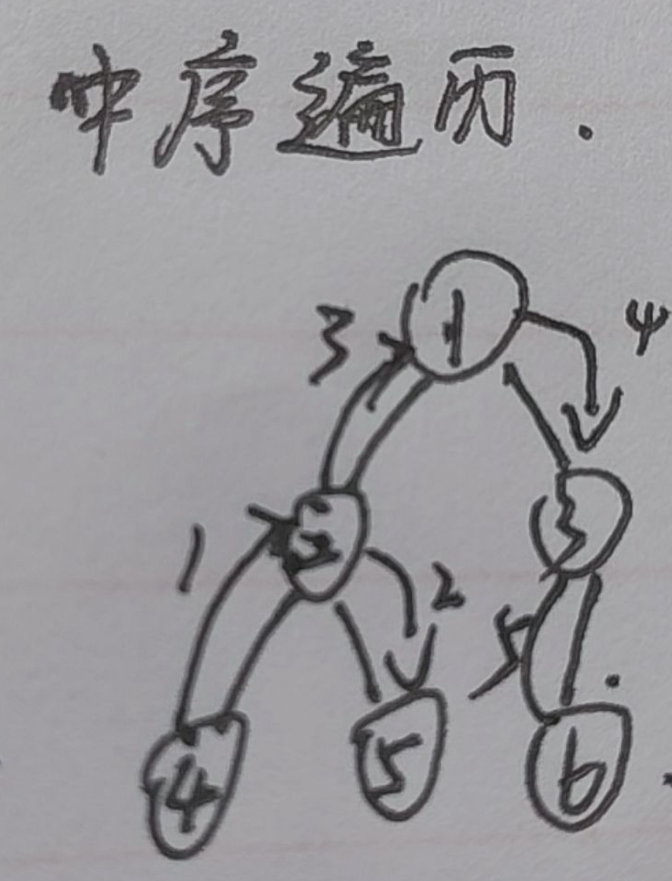
从代码的角度来理解,先将1这个根节点传入,接着判断指针的存在,再递归将左子树的指针传入。就这样,一直传入,知道有一个的左子树无子树后返回到上一个作为子树的进行访问,从左到根再到右,其例子遍历结果:4 2 5 1 3 6.总的来说就是找树的最底下最左边的遍历开始,再按照左根右的遍历方式进行遍历。
🌆二叉树后序遍历
// 二叉树后序遍历
void PostOrder(BTNode* root)
{if(root == NULL){printf("NULL");return;}PostOrder(root->left);PostOrder(root->right);printf("%d",root->data);
}
对于后序遍历,就是左右根,跟中序遍历差不多,就是找最底下的最左边的开始,再从右到根。像中序遍历的例子里,用后序遍历,其遍历的结果是:4 5 2 3 1 6。
🌆二叉树的层序遍历
// 层序遍历
void LevelOrder(BTNode* root)
{ Queue q;QueueInit(&q);if (root){QueuePush(&q, root);}while(!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);printf("%d ", front->data);if (front->left)QueuePush(&q, front->left);if (front->right)QueuePush(&q, front->right);}printf("\n");QueueDestroy(&q);
}
对于层序遍历,从他的名字上就可以看的出他是一层一层的访问,这时候我们就要用到之前学的队列了,首先我们先将队列实例化,接着判断root的存在,进而将根插入队列,接着用循环来进行每层的插入,在这个循环里先将队头的数据用一个新建变量来存储,再进行打印,这样就进行了遍历。
🌆二叉树节点个数
int BinaryTreeSize(BTNode* root)
{return !root? 0: BinaryTreeSize(root->left)+BinaryTreeSize(root->right)+1;
}
对于计算二叉树的节点数,我们肯定是要遍历二叉树的,而遍历就要有我们的递归了,对于二叉树我们要有所判断是否为空树。对于空树就是0,反之我们通过递归,计算左右子树的大小,再加1(根节点)。
🌆二叉树叶子节点个数
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{if (root == NULL) {return 0;}if (root->left == NULL && root->right == NULL){return 1;}return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}
对于叶子结点个数,我们先要看叶节点有什么特点:就是无左右子树。对于这一特点,我们可以利用来判断递归遍历到一个结点来判断他是否为叶节点,如果是就返回1.其实就是最底层的节点数,我们可以用寻找每一层的结点数函数来代替。
🌆二叉树第k层节点个数
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{assert(k > 0);if (root == NULL){return 0;}if (k == 1){return 1;}return TreeKLevel(root->left, k - 1)+ TreeKLevel(root->right, k - 1);
}
对于计算k层的节点数,我们可以这么理解。假设我们要计算第n层的结点数,我们肯定需要递归遍历来找到第n层,这时到第n层我们就需要一个条件来判断他是否有结点,这时我们就可以用k这一个参数来做条件,比如说我们的递归,每进行一次递归就是下一层,这时就能够用k==1来判断有结点了。这里我们还要考虑传入的root为空的情况,为空就是没节点。
🌆二叉树查找值为x的节点
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{if (root == NULL)return NULL;if (root->data == x)return root;BTNode* lret = TreeFind(root->left, x);if (lret)return lret;BTNode* rret = TreeFind(root->right, x);if (rret)return rret;return NULL;
}
对于二叉树查找值为x的结点,那么我们肯定又少不了递归遍历了和判断条件了。就如上述代码,判断条件就是通过root 和root指向的data来判断,紧接着就是通过递归遍历再创建一个新变量来接收传来的结点,再进行判断是否为空。如果没x,就返回NULL。
🌆判断二叉树是否是完全二叉树
// 判断二叉树是否是完全二叉树
int BinaryTreeComplete(BTNode* root)
{Queue q;QueueInit(&q);if (root){QueuePush(&q, root);}while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);if (front == NULL){break;}else{QueuePush(&q, front->left);QueuePush(&q, front->right);}}// 判断是不是完全二叉树while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);// 后面有非空,说明非空节点不是完全连续if (front){QueueDestroy(&q);return false;}
}
对于判断是不是完全二叉树,你们想我们的层序遍历时不是很好,对于将完全二叉树的数据传入队列中那队列里有数据的中间就不可能为空。所以我们先建队列将数据传入 若传入的是空,那么就跳出第一个循环,在通过另一个循环来判断后面的数据 一旦遇到空节点,后续必须全为空;若后续还有非空,才说明不是完全二叉树。
🌆二叉树销毁
// 二叉树销毁
void BinaryTreeDestory(BTNode* root)
{if (root == NULL){return;}// 先销毁左子树BinaryTreeDestroy(root->left);// 再销毁右子树BinaryTreeDestroy(root->right);// 最后释放当前节点free(root);
}
简单来说就是递归遍历销毁。
🌆通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi)
{// 检查是否越界或遇到空节点标识if (*pi >= n || a[*pi] == '#'){(*pi)++;return NULL;}// 创建当前节点BTNode* root = (BTNode*)malloc(sizeof(BTNode));root->data = a[*pi];(*pi)++;// 递归创建左子树root->left = BinaryTreeCreate(a, n, pi);// 递归创建右子树root->right = BinaryTreeCreate(a, n, pi);return root;/*pi >= n:索引越界(遍历完数组),说明当前子树为空。a[*pi] == '#':遇到空节点标识 #,说明当前子树为空。(*pi)++:索引后移(跳过空节点或越界位置)。return NULL:返回空指针,表示当前节点不存在(空树)malloc:动态分配一个 BTNode 节点内存,用于存储当前二叉树节点。root->data = a[*pi]:用数组当前元素(非 #)初始化节点数据。(*pi)++:索引后移,准备处理下一个元素(构建子树)。按照前序遍历规则,当前节点创建后,先递归构建左子树。pi 是指针,递归调用时会同步修改索引,保证左右子树遍历 “接力”当前节点的左、右子树构建完成后,返回当前节点指针,让父节点连接自己。*/
}
a储存的是 ABD##E#H##CF##G##。
递归构建二叉树,pi 是数组索引的指针,用于在递归过程中同步移动索引。
遇到 # 时返回 NULL,表示空节点,否则创建新节点,依次递归构建左、右子树。
🌄完整代码实现
🌆Queue.h文件
#pragma once#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#include<assert.h>typedef struct BinaryTreeNode* QDatatype;typedef struct QueueNode
{struct QueueNode* next;QDatatype data;
}QNode;typedef struct Queue
{QNode* head;QNode* tail;int size;
}Queue;
void QueueInit(Queue* pq);
void QueueDestroy(Queue* pq);
void QueuePush(Queue* pq, QDatatype x);
void QueuePop(Queue* pq);
int QueueSize(Queue* pq);
bool QueueEmpty(Queue* pq);
QDatatype QueueFront(Queue* pq);
QDatatype QueueBack(Queue* pq);🌆Queue.c文件
#include"Queue.h"void QueueInit(Queue* pq)
{assert(pq);pq->head = pq->tail = NULL;pq->size = 0;
}void QueueDestroy(Queue* pq)
{assert(pq);QNode* cur = pq->head;while (cur){QNode* next = cur->next;free(cur);cur = next;}pq->head = pq->tail = NULL;pq->size = 0;
}void QueuePush(Queue* pq, QDatatype x)
{QNode* newnode = (QNode*)malloc(sizeof(QNode));if (newnode == NULL){perror("malloc fail");return;}newnode->data = x;newnode->next = NULL;if (pq->head == NULL){assert(pq->tail == NULL);pq->head = pq->tail = newnode;}else{pq->tail->next = newnode;pq->tail = newnode;}pq->size++;
}void QueuePop(Queue* pq)
{assert(pq);assert(pq->head != NULL);/*QNode* next = pq->head->next;free(pq->head);pq->head = next;if (pq->head == NULL)pq->tail = NULL;*/if (pq->head->next == NULL){free(pq->head);pq->head = pq->tail = NULL;}else{QNode* next = pq->head->next;free(pq->head);pq->head = next;}pq->size--;
}int QueueSize(Queue* pq)
{assert(pq);return pq->size;
}bool QueueEmpty(Queue* pq)
{assert(pq);return pq->size == 0;
}QDatatype QueueFront(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));return pq->head->data;
}QDatatype QueueBack(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));return pq->tail->data;
}
🌆BinaryTree.h文件
#pragma once#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#include<assert.h>
typedef int BTDataType;
typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;
//创建一个新结点
BTNode* BuyNode(BTDataType x);
// 二叉树前序遍历
void PreOrder(BTNode* root);
// 二叉树中序遍历
void InOrder(BTNode* root);
// 二叉树后序遍历
void PostOrder(BTNode* root);
// 层序遍历
void LevelOrder(BTNode* root);
// 二叉树节点个数
int BinaryTreeSize(BTNode* root);
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root);
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k);
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);
// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi);
// 二叉树销毁
void BinaryTreeDestory(BTNode* root);
// 判断二叉树是否是完全二叉树
bool BinaryTreeComplete(BTNode* root);🌆BinaryTree.c文件
#include "BinaryTree.h"
#include "Queue.h"
BTNode* BuyNode(BTDataType x)
{BTNode* node = (BTNode*)malloc(sizeof(BTNode));if (node == NULL){perror("malloc fail");return NULL;}node->data = x;node->left = NULL;node->right = NULL;return node;
}
// 二叉树前序遍历
void PreOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}printf("%d ", root->data);PreOrder(root->left);PreOrder(root->right);
}
// 二叉树中序遍历
void InOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}InOrder(root->left);printf("%d ", root->data);InOrder(root->right);
}
// 二叉树后序遍历
void PostOrder(BTNode* root)
{if (root == NULL){printf("NULL ");return;}PostOrder(root->left);PostOrder(root->right);printf("%d ", root->data);
}
// 层序遍历
void LevelOrder(BTNode* root)
{Queue q;QueueInit(&q);if (root){QueuePush(&q, root);}while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);printf("%d ", front->data);if (front->left)QueuePush(&q, front->left);if (front->right)QueuePush(&q, front->right);}printf("\n");QueueDestroy(&q);
}int BinaryTreeSize(BTNode* root)
{return !root? 0: BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}
// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{if (root == NULL){return 0;}if (root->left == NULL && root->right == NULL){return 1;}return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}
// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{assert(k > 0);if (root == NULL){return 0;}if (k == 1){return 1;}return BinaryTreeLevelKSize(root->left, k - 1)+ BinaryTreeLevelKSize(root->right, k - 1);
}
// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{if (root == NULL)return NULL;if (root->data == x)return root;BTNode* lret = BinaryTreeFind(root->left, x);if (lret)return lret;BTNode* rret = BinaryTreeFind(root->right, x);if (rret)return rret;return NULL;
}
// 判断二叉树是否是完全二叉树
bool BinaryTreeComplete(BTNode* root)
{Queue q;QueueInit(&q);if (root){QueuePush(&q, root);}while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);if (front == NULL){break;}else{QueuePush(&q, front->left);QueuePush(&q, front->right);}}// 判断是不是完全二叉树while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);// 后面有非空,说明非空节点不是完全连续if (front){QueueDestroy(&q);return false;}}QueueDestroy(&q);return true;
}// 二叉树销毁void BinaryTreeDestory(BTNode* root){if (root == NULL){return;}// 先销毁左子树BinaryTreeDestory(root->left);// 再销毁右子树BinaryTreeDestory(root->right);// 最后释放当前节点free(root);}// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树BTNode* BinaryTreeCreate(BTDataType * a, int n, int* pi){// 检查是否越界或遇到空节点标识if (*pi >= n || a[*pi] == '#'){(*pi)++;return NULL;}// 创建当前节点BTNode* root = (BTNode*)malloc(sizeof(BTNode));if (root == NULL){perror("malloc failed");return NULL;}root->data = a[*pi];(*pi)++;// 递归创建左子树root->left = BinaryTreeCreate(a, n, pi);// 递归创建右子树root->right = BinaryTreeCreate(a, n, pi);return root;}🌆test.c文件
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
// 假设你的二叉树头文件和队列头文件长这样
#include "BinaryTree.h"
#include "Queue.h" int main() {// 前序数组:'#' 表示空节点,可根据需求调整BTDataType preorder[] = { '1', '2', '3', '#', '#', '4', '#', '#', '5', '6', '#', '#', '#' };int pi = 0;// 构建二叉树BTNode* root = BinaryTreeCreate(preorder, sizeof(preorder) / sizeof(preorder[0]), &pi);printf("前序遍历:");PreOrder(root);printf("\n");printf("中序遍历:");InOrder(root);printf("\n");printf("后序遍历:");PostOrder(root);printf("\n");printf("层序遍历结果为:");LevelOrder(root);printf("\n");printf("二叉树节点个数为:%d\n", BinaryTreeSize(root));printf("二叉树叶子节点个数为:%d\n", BinaryTreeLeafSize(root));printf("二叉树第 3 层节点个数为:%d\n", BinaryTreeLevelKSize(root, 3));printf("二叉树是否是完全二叉树:%s\n",BinaryTreeComplete(root) ? "是" : "不是");// 查找节点测试BTNode* findNode = BinaryTreeFind(root, '4');if (findNode) {printf("找到值为 '4' 的节点啦~\n");}else {printf("未找到值为 '4' 的节点~\n");}// 销毁二叉树BinaryTreeDestory(root);return 0;
}
❤️总结
文字的旅程暂告段落,感谢你温柔相伴。若文中有疏漏,盼你轻声指正,那是成长的微光。倘若这些字句,曾为你拂去些许迷茫,不妨留个赞,让温暖延续,也欢迎你常来,共赴文字的山海,聆听心灵的回响❤️
