【第二章-数据的表示和运算】

1. 数制与编码

1.1 进位计算制及其相互转换

1. 采用二进制编码的原因

• 二进制只有两种状态，使用两个稳定状态的物理器件就可以表示二进制数的每一位，制造成本低。
• 二进制的1和0刚好与逻辑值真和假相对应。为计算机实现逻辑运算和程序逻辑判断提供了便利条件。
• 二进制编码和运算的规则简单，通过逻辑门电路方便实现算术运算。
  该题答案为D。

2. 进位计数制

• 常用的进位制有二进制、十进制、八进制、十六进制等。生活中一般是十进制，计算机中通常有二进制、八进制、十六进制。
• 在进位计数制中，每个数位所用到的不同数码的个数称为基数。比如10进制的基数为10，有(0~9)10个数字。逢十进一。
• 每个数码所表示的数值等于该数码乘以一个与它所在数位有关的常数，这个常数称为位权。
• 二进制中的3位数码编为一组就是1位八进制，4位编为一组就是1位16进制。
• B表示二进制，O表示八进制，D表示十进制一般省略，H一般是十六进制，也可以用前缀0x表示十六进制。

3. 不同进制之间的相互转换

• 二进制转八进制和十六进制。如果转换为八进制则3位分为一组，转换为十六进制则4位分为一组。不够时，从左边用0补齐。
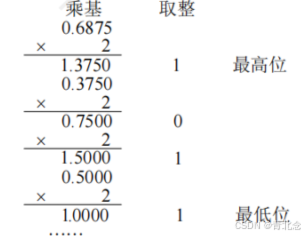
• 如1111000010.01101转换为八进制和十六进制
  八进制 【001,111,000,010.011,010】=1702.32O
  十六进制【0011,1100,0010.0110,1000】=3C2.68
• 其中10进制数123.6875转二进制中的小数部分是通过每次×基数2得到。
  

1.2 定点数的编码表示

1. 真值和机器数。生活中通常用正负号来表示正数和负数。如+15，-8等。这种带+正号或者-负号的数称为真值。真值是机器数所代表的实际值。计算机中将数的符号和数值一起编码，将数据的符号数字化，通常0代表正数，1代表负数。这种把符号数字化的数称为机器数。常用的有原码、补码、反码表示法。如0,101表示+5，这里的逗号，用于区分符号位与数值位。
2. 机器数的定点表示。根据小数点的位置是否固定，计算机中有两种数据格式，定点表示和浮点表示。在现代计算机中，通常用补码表示整数，用原码小数表示浮点数的尾数部分，用移码表示浮点数的阶码部分。

• 在计算机中，数字的表示方法主要分为定点数（Fixed-Point）和浮点数（Floating-Point）两种。它们的核心区别在于小数点的位置是否固定，这直接影响数值的表示范围、精度和计算方式。
• 定点小数：定点小数是纯小数，约定小数点位置在符号位之后。
• 定点整数：定点整数时纯整数，约定小数点位置在有效数值部分最低为之后。
• 要明白机器内部并没有小数点，只是认为约定了小数点的位置。因此在定点数的编码和运算中不用考虑对应的时定点小数还是定点整数，只需要关心它们的符号位和数值位即可。定点数的编码表示法有4种：原码、补码、反码和移码。

3. 原码、补码、反码和移码

• 原码：用机器数的最高位表示数的符号，其余各位表示数的绝对值。如x1=+1110,x2=-1110，字长位8位，则x1原码为：0,0001110,x2原码为1,0001110,其中最高位为符号位。【原码的优点:①与真值对应关系简单，直观，与真值的转换简单②用原码实现乘除运算比较简单】【原码的缺点：①0的表示不唯一，有+0和-0两个编码②用原码实现加减法运算比较复杂】
• 补码:补码表示法种的加减法运算统一采用加法操作实现，正数的补码和原码相同，负数的补码等于负数的绝对值对应的原码取反+1。补码的表示范围如果字长为n+1，则补码表示的范围是-2ⁿ~2ⁿ-1。
• 反码：负数的反码为按位取反不加1.正数的原码反码补码都相同。反码的缺点：①0的表示不唯一存在+0和-0②表示范围比补码少一个最小负数，因此反码在计算机种很少使用。
• 移码：移码通常用来表示浮点数的阶码，只能表示整数。移码就是给所有数字统一加上一个固定值（如+127），把负数变成正数，方便计算机直接比较大小。（就像给全班考试成绩都+60分，保证没有不及格，排序时分数高的真实值一定更大）
  【补码和移码通过取消重复的“-0”，把省下来的编码名额送给-128（补码）或+128（移码），所以能比原码多表示一个数！】

4. 补码大小判断

• 原码、补码、反码的符号位相同，正数的机器码相同。
• 原码、反码的表示在数轴上对称，二者都存在+0和-0两个0。
• 补码和移码的表示在数轴上不对称，0的表示唯一，他们比原码和反码多表示一个数。
• 原码很容易判断大小。而负数的补码和反码很难直接判断大小，对于负数，数值位部分越小，则其绝对值越大，即负的越多。

5. 注意点【原码、补码、反码、移码的表示范围】：

• 对于原码：如果字长为n+1，则原码表示的整数范围是-(2ⁿ-1)~2ⁿ-1 。以8位表示为例，则为-127至+127。0浪费了两个，有+0和-0的区别。
• 对于补码：如果字长为n=1，则补码整数的表示范围是-2ⁿ~2ⁿ-1 ，比原码多表示一个-2ⁿ，以8位表示为例将-0的表示给-128了。
• -128的补码（8位）：
  正常补码范围是-127～+127
  但计算机"偷"了一个编码：把原本表示-0的10000000重新定义为-128
  这样8位补码就能表示-128～+127共256个数
  这就是为什么补码能比原码多表示一个数
• 对于移码：以8位表示为例，表示范围是–2ⁿ~2ⁿ-1
  【来自里昂学长的课程图】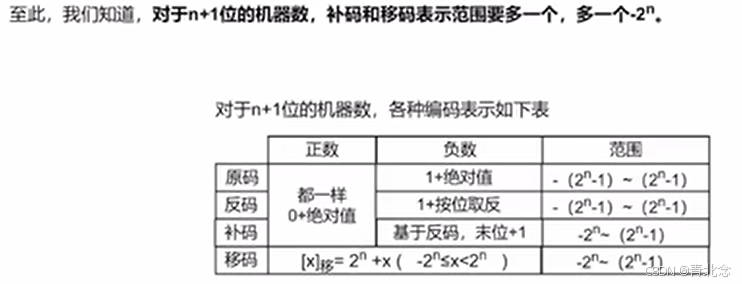

1.3 整数的表示

1. 无符号整数的表示

• 当一个编码的全部二进制位均为数值位没有符号位时吗，该编码就是无符号整数。
• 对于8位无符号整数，表示范围是0至255，对于有符号整数位-128至+127。

2. 有符号整数的表示

• 将符号位数值化，并将符号位放在有效数字前面，就组成了有符号整数。对于原码、补码、反码和移码的表示种，补码表示有符号整数具有优势因为①与原码和反码相比，0的补码表示唯一，00000000，而10000000=-128。②与原码和移码相比，补码运算规则简单，且符号位和数值位可以一起参加运算。③与原码和反码相比，补码比原码和反码多表示一个最小负数，以8位为例就是多了-0的表示，10000000=-128，将-0的表示代表-128.
• 计算机种有符号整数都用补码表示，所以n位有符号整数的表示范围是-2^n-1~2^n-1-1

1.4 C语言中的整数类型及类型转换

1. C语言中的整形数据类型

• C语言中要使用无符号类型要在前面添加unsigned的标识符，如果不指定则默认是有符号整数。
• 字符型一个字节8位是C语言中特殊的类型，默认按照无符号整数解释。
• 对于short、int、long、char这些类型都是按照补码形式存储的。只是有符号整数的最高位待变符号，无符号全部二进制位都代表数值，，没有绝对值。对于有符号和无符号的数表示的数据范围是不同的。

2. 有符号数和无符号数之间的转换

• 对于无符号short x=-4321进行unsigned short y=(unsigned short)x;后得到的y值为y=61215。
  也就是说位数相同进行强制转换后，每位对应都是相同的，仅仅改变解释这些位的方式。
• 对于无符号数65535与有符号数-1进行比较也可以看到补码除最高位都是15位1。也就是无符号数转有符号数与有符号数转换为无符号数都会发生数值的变化。
• 注意：如果同时有无符号数与有符号数参与运算，C语言标准规定按照无符号数进行运算。

3. 不同字长整数之间的转换

• 常见的运算是在不同字长的整数之间进行类型转换的。当出现大字长向小字长转换时，如int x=165537 short y=(short) x。最后y的值位=-31071原因是系统把多余的高位部分直接截断，低位部分直接赋值。得到的补码是165537的低16位，取反+1后得到-31071。
  165537的补码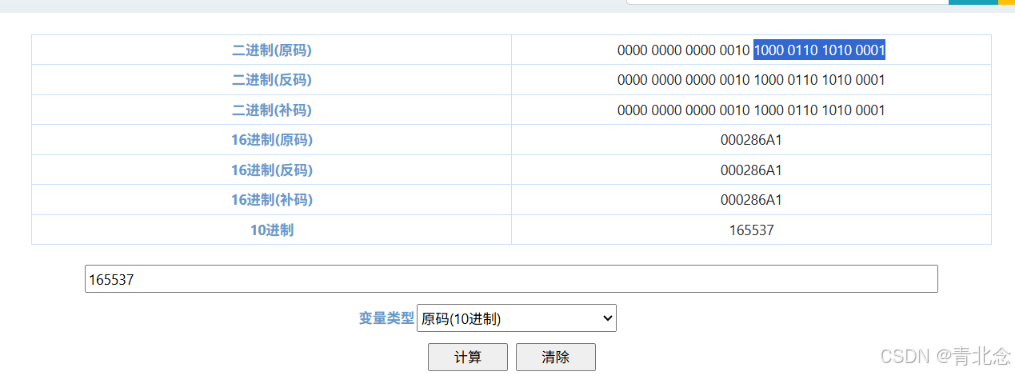
  低16位为1000 0110 1010 0001
  得到-31071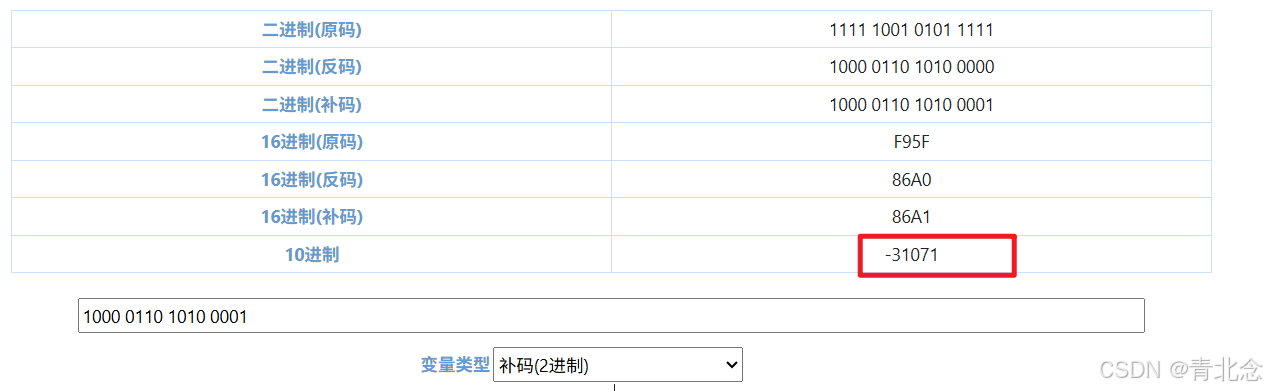
• 当出现小字长向大字长转换时，如果原数字时无符号整数，则高位进行零扩展。如果原数字是有符号整数，进行符号扩展，比如16位有符号整数x强制转换为32位有符号y时，因为x符号位是1，所以高16位用1补充。注意char型为8位无符号整数，在其转换为int时高位补0即可。
• 总结：当有符号数和无符号数转换中，如果两个变量的字长不同，则分两种情况讨论。①小字节转大字节则需要进行扩展，如果原数字是无符号则进行0扩展。如果原数字是有符号则进行符号扩展。②大字长转换为小字长，则直接截取低位部分，得到补码，要想得到原值，要进行补码取反+1的操作。

1.5 小结

2. 运算方法和运算电路

3. 浮点数的表示和运算

4. 小结