当前位置：首页 > news >正文

CF每日5题（1500-1600）

news 2025/7/27 9:00:57

2A map 模拟 1500

map水题，先找最大值，再走一遍所有回合找最先到最大值的人
但是一开始忽略了会有加到最大值之后又减下来的情况

struct per
{string nm;int sc;
};
map<string,int>m;
map<string,int>mp;
void solve()
{int n;cin>>n;vector<per>rd(n+1);forr(i,1,n){cin>>rd[i].nm>>rd[i].sc;m[rd[i].nm]+=rd[i].sc;// mx=max(mx,m[rd[i].nm]);}int mx=-1e9;for(auto i:m){mx=max(mx,i.second);}forr(i,1,n){mp[rd[i].nm]+=rd[i].sc;// cout<<rd[i].nm<<' '<<mp[rd[i].nm]<<endl;if(m[rd[i].nm]==mx&&mp[rd[i].nm]>=mx)return cout<<rd[i].nm<<endl,void();}
}

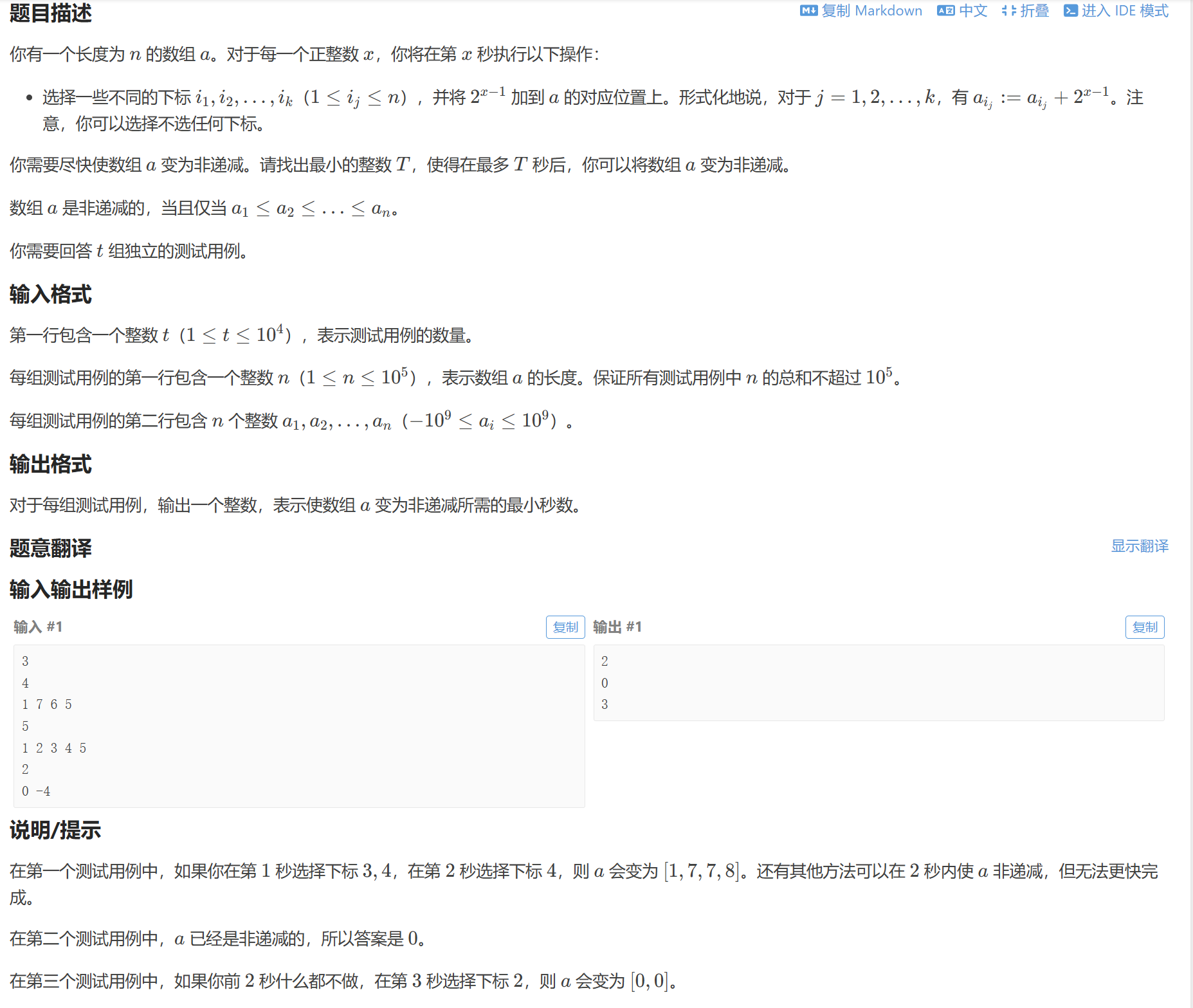
一开始读了假题…以为每秒只能选一个坐标…
题意：在第x秒可以选择多个坐标上的数 $2^{x-1}$
$1,2,4,8,....,2^{x-1}$ 可以组成 $1,2^x-1]$ 之内的所有数，设 $tp_i=a[i-1]-a[i]$ ，能满足 $tpmax∈[1,2x−1],tpmax≤2x−1tp_{max}\in [1,2^x-1],tp_{max}\leq 2^x-1$ 即可，即 $x=log_2(tp_{max}+1)$

void solve(){int n;cin>>n;vector<int>a(n+1);int mx=0;forr(i,1,n){cin>>a[i];if(i>1&&a[i]<a[i-1]){mx=max(mx,a[i-1]-a[i]);a[i]=a[i-1];}}// cout<<mx<<endl;int x=ceil(log2(mx+1));cout<<x<<endl;
}

1526C1 1500

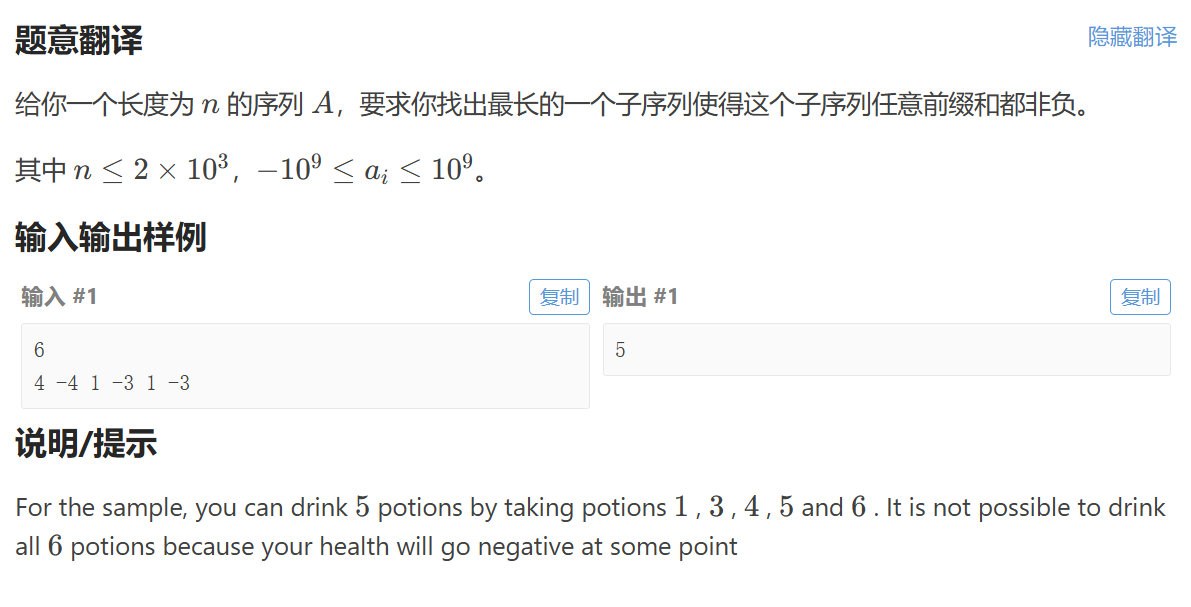
O(n2) dp做法

int dp[N];//dp[i] i长度的子序列前缀和是dp[i]
void solve(){int n;cin>>n;vector<int>a(n+1);forr(i,1,n){cin>>a[i];dp[i]=-inf;//注意初始化}dp[0]=0;forr(i,1,n){//枚举每一瓶毒药reforr(j,1,i){//从上一瓶毒药状态转移过来 滚动数组注意从后往前更新if(dp[j-1]+a[i]>=0){//保证子序列的每一个前缀和非负dp[j]=max(dp[j-1]+a[i],dp[j]);//取max因为让前缀和尽量非负 这样能找出最长的序列}}}// forr(i,1,n)cout<<dp[i]<<' ';cout<<endl;reforr(i,0,n){//注意这里i左边界在0 因为可能有全是负的情况if(dp[i]>=0)return cout<<i<<endl,void();}
}

O(nlogn) 反悔贪心做法

针对C2 2e5数量级

void solve(){int n;cin>>n;priority_queue<int,vector<int>,greater<int> >q;vector<int>a(n+1);forr(i,1,n){cin>>a[i];}int sum=0;forr(i,1,n){sum+=a[i];//先放进去q.push(a[i]);if(sum<0){//如果前缀和为负// if(q.empty())continue;int tp=q.top();//把前面拖后腿的拿出来q.pop();sum-=tp;}}cout<<q.size()<<endl;
}

一开始是这样写的不知道为什么会wa3 感觉大差不差TAT

void solve(){int n;cin>>n;priority_queue<int,vector<int>,greater<int> >q;vector<int>a(n+1);forr(i,1,n){cin>>a[i];}int sum=0,ans=0;forr(i,1,n){if(sum+a[i]>=0){sum+=a[i];q.push(a[i]);}else{if(q.empty())continue;int tp=q.top();q.pop();sum-=tp;q.push(a[i]);sum+=a[i];}}cout<<q.size()<<endl;}

371C 暴力 1600

老八秘制小汉堡，既提神，又补脑。

写成石山了

int rq[4],n[4],p[4];
map<char,int>m={{'B',1},{'S',2},{'C',3}};
void solve(){string s;cin>>s;forr(i,1,3)cin>>n[i];forr(i,1,3)cin>>p[i];int r;cin>>r;for(auto i:s){rq[m[i]]++;//require}int ans=0,mn=1e9;forr(i,1,3){if(rq[i]==0)continue;int tp=n[i]/rq[i];mn=min(mn,tp);}ans+=mn;int mx=0;forr(i,1,3){if(rq[i]==0)continue;n[i]-=mn*rq[i];mx=max(n[i]/rq[i],mx);}// cout<<mx<<endl;forr(i,1,mx+1){int nd1=max(0ll,rq[1]-n[1]);n[1]=max(0ll,n[1]-rq[1]);int nd2=max(0ll,rq[2]-n[2]);n[2]=max(0ll,n[2]-rq[2]);int nd3=max(0ll,rq[3]-n[3]);n[3]=max(0ll,n[3]-rq[3]);r-=(p[1]*nd1+p[2]*nd2+p[3]*nd3);if(r>=0)ans++;else break;}if(r>0)ans+=(r/(p[1]*rq[1]+p[2]*rq[2]+p[3]*rq[3]));cout<<ans<<endl;
}

431C dp 1600

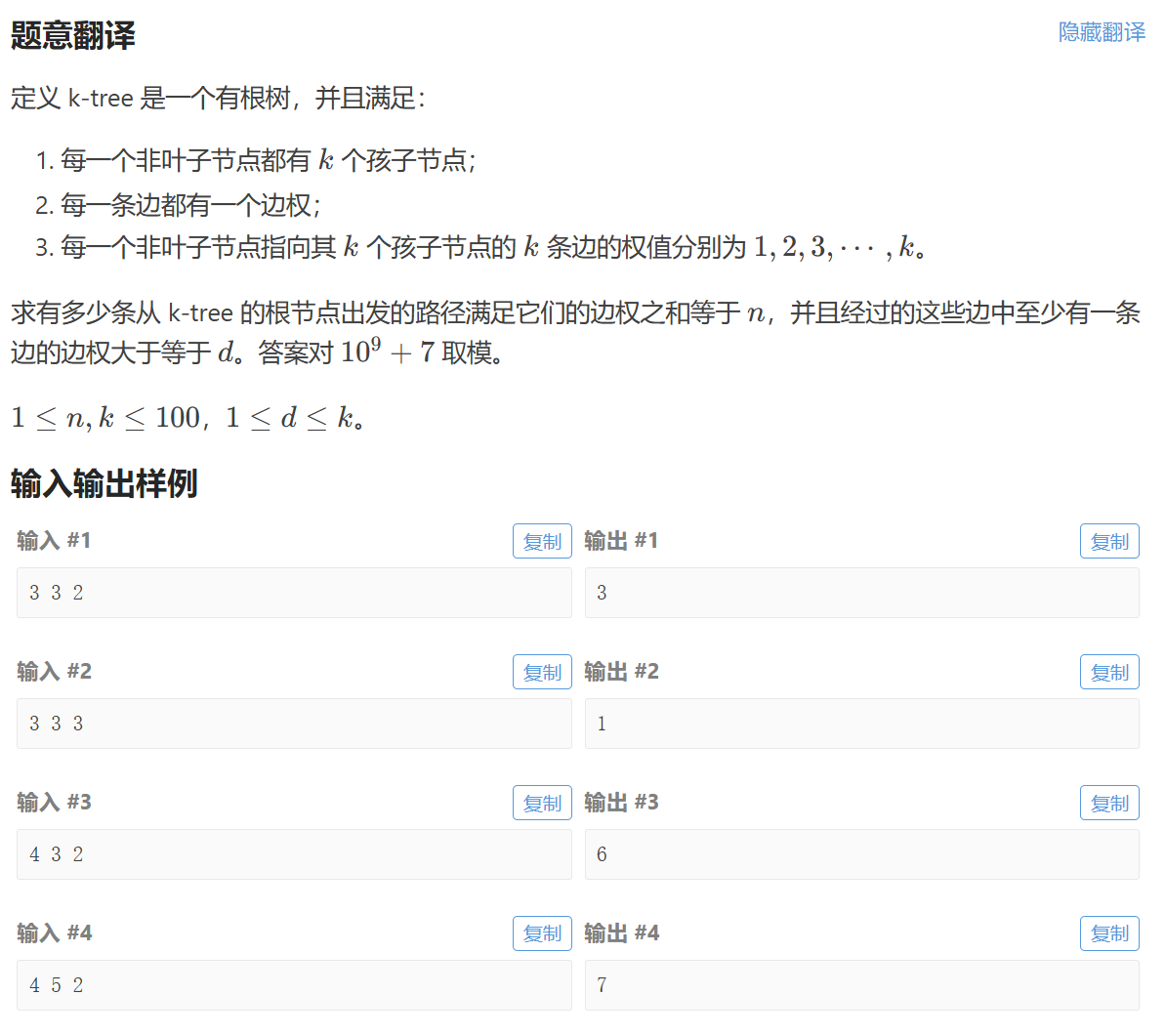
dp[i][0]是路上还没有 $≥d\geq d$ 的路径，和为i的位置
dp[i][1]是有 $≥d\geq d$ 的合法路径

int dp[N][3];
void solve(){int n,k,d;cin>>n>>k>>d;dp[0][0]=1;forr(i,1,n){forr(j,1,min(i,k)){dp[i][1]=(dp[i][1]+dp[i-j][1])%mod;//合法的转移到合法的if(j>=d){dp[i][1]=(dp[i][1]+dp[i-j][0])%mod;//不合法的+(>=d)的变合法}else{dp[i][0]=(dp[i][0]+dp[i-j][0])%mod;//不合法的转移到不合法的}}}cout<<dp[n][1]<<endl;
}