最小生成树:Kruskal与Prim算法
最小生成树:Kruskal与Prim算法
想象一下,你是一个城市规划师,需要在城市的不同区域之间铺设水管或电缆。为了节省成本,你希望用最少的材料连接所有区域,同时确保每个区域都能被连接到。这正是最小生成树(MST)算法要解决的问题!
最小生成树(Minimum Spanning Tree)是图论中的一个经典问题,它在网络设计、电路布线、交通规划等领域有着广泛的应用。今天,我们将深入探讨两种最著名的MST算法:Kruskal算法和Prim算法。
1. 最小生成树基础概念
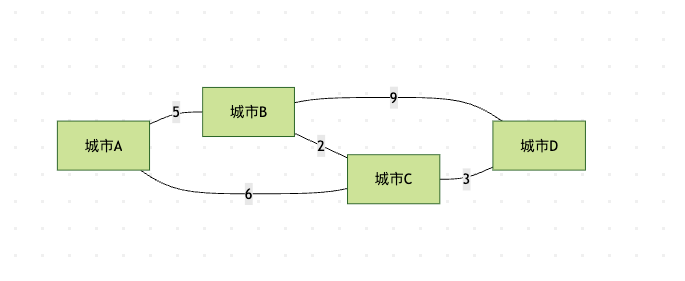
上图展示了一个简单的城市连接图,边上的数字表示建设道路的成本。我们的目标是选择一组边,连接所有城市,同时使总成本最小。
最小生成树的定义
对于给定的连通无向图G=(V,E),其中V是顶点集合,E是边集合,最小生成树T是G的一个子图,满足:
- T包含G的所有顶点
- T是一棵树(无环且连通)
- T中所有边的权重之和最小
2. Kruskal算法
理解了最小生成树的概念后,我们来看第一种算法——Kruskal算法。这个算法由Joseph Kruskal在1956年提出,它的核心思想是"贪心地选择不会形成环的最小权重边"。
Kruskal算法执行流程
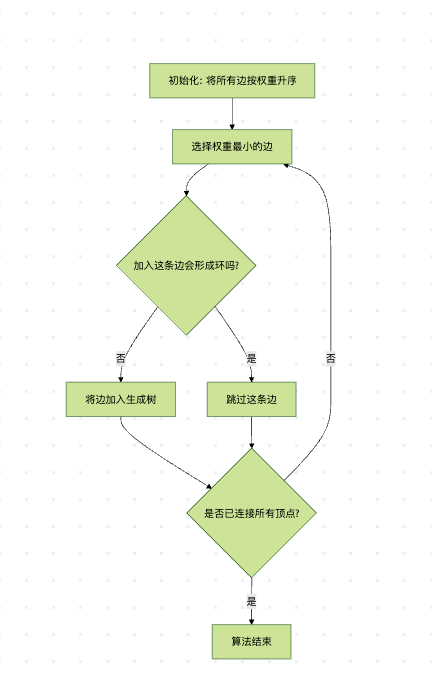
以上流程图说明了Kruskal算法的基本执行过程:不断选择最小的边,只要不形成环就加入生成树,直到所有顶点都被连接。
Kruskal算法实现
Kruskal算法的实现需要用到并查集(Union-Find)数据结构来高效地检测环。下面是Python实现:
class UnionFind:def __init__(self, size):self.parent = list(range(size))def find(self, x):if self.parent[x] != x:self.parent[x] = self.find(self.parent[x])return self.parent[x]def union(self, x, y):x_root = self.find(x)y_root = self.find(y)if x_root == y_root:return False # 已经在同一集合,会形成环self.parent[y_root] = x_rootreturn Truedef kruskal(graph):edges = []for u in range(len(graph)):for v, weight in graph[u]:if u < v: # 避免重复添加边edges.append((weight, u, v))edges.sort() # 按权重排序uf = UnionFind(len(graph))mst = []for weight, u, v in edges:if uf.union(u, v):mst.append((u, v, weight))if len(mst) == len(graph) - 1:breakreturn mst
上述代码实现了Kruskal算法,使用并查集来检测环。算法首先将所有边按权重排序,然后依次尝试将边加入生成树,直到连接所有顶点。
Kruskal算法原理详解
让我们用一个生活案例来理解Kruskal算法:假设你是一个快递公司的经理,需要在多个城市建立配送中心并连接它们。你的预算是有限的,所以希望用最少的成本连接所有城市。
- 收集所有可能的路线:首先列出所有城市之间的道路及其建设成本。
- 按成本排序:将这些道路从便宜到昂贵排序。
- 逐步选择道路:从最便宜的开始,选择那些不会形成环路的道路。
- 完成连接:当所有城市都被连接时停止,即使还有更贵的道路未被考虑。
为什么Kruskal算法能保证找到最小生成树? 因为算法总是选择当前可用的最小权重边,且不会形成环,这保证了最终结果的全局最优性。
3. Prim算法
了解了Kruskal算法后,我们来看第二种方法——Prim算法。这个算法由捷克数学家Vojtěch Jarník在1930年提出,后来被Robert Prim在1957年重新发现。
Prim算法执行流程
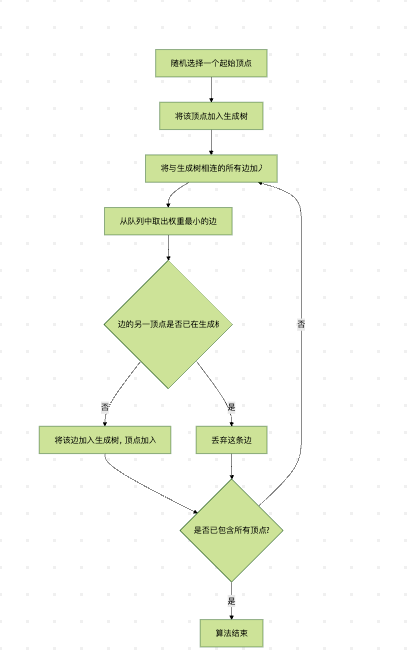
以上流程图展示了Prim算法的执行过程:从一个顶点开始,逐步扩展生成树,每次都选择连接生成树和外部顶点的最小权重边。
Prim算法实现
Prim算法通常使用优先队列(最小堆)来实现。下面是Python实现:
import heapqdef prim(graph):mst = []visited = set()start_vertex = 0visited.add(start_vertex)edges = [(weight, start_vertex, to)for to, weight in graph[start_vertex]]heapq.heapify(edges)while edges and len(visited) < len(graph):weight, u, v = heapq.heappop(edges)if v not in visited:visited.add(v)mst.append((u, v, weight))for to, weight in graph[v]:if to not in visited:heapq.heappush(edges, (weight, v, to))return mst
这段代码实现了Prim算法,使用最小堆来选择当前可用的最小权重边。算法从一个顶点开始,逐步扩展生成树,直到包含所有顶点。
Prim算法原理详解
继续用快递公司的例子来解释Prim算法:这次你决定从一个城市开始,逐步扩展配送网络。
- 选择一个起点:比如从北京开始建设配送中心。
- 寻找最近的连接:从北京出发,找到建设成本最低的连接路线(比如北京到天津)。
- 扩展网络:现在你的网络包含北京和天津,寻找连接这两个城市与其他城市的最便宜路线。
- 重复扩展:持续这个过程,每次都选择连接现有网络和外部城市的最便宜路线。
- 完成网络:当所有城市都被包含在网络中时停止。
Prim算法与Kruskal算法的直观区别:Kruskal算法是"全局"选择边,而Prim算法是"局部"扩展,从一个点开始逐步生长。
4. 算法比较与选择
现在我们已经了解了两种算法,让我们比较它们的特性和适用场景。
| 比较项 | Kruskal算法 | Prim算法 |
|---|---|---|
| 时间复杂度 | O(E log E) 或 O(E log V) | O(E log V) (使用优先队列) |
| 空间复杂度 | O(E) | O(V) |
| 适用图类型 | 稀疏图(边较少) | 稠密图(边较多) |
| 实现难度 | 需要实现并查集 | 需要优先队列 |
| 并行潜力 | 较高(边可以并行处理) | 较低(顺序扩展) |
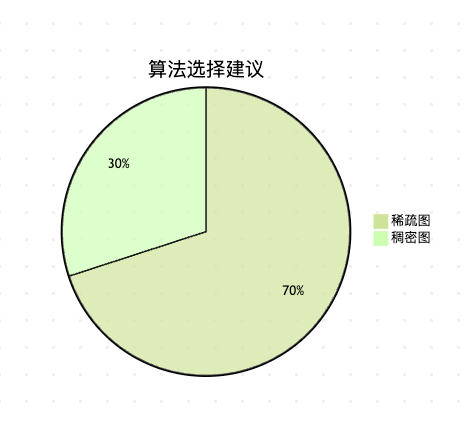
这个饼图展示了算法选择的建议:对于边数远小于顶点数平方的稀疏图,Kruskal通常更高效;对于边数接近完全图的稠密图,Prim算法可能更合适。
5. 实际应用案例
让我们看一个具体的例子,比较两种算法在实际图中的表现。
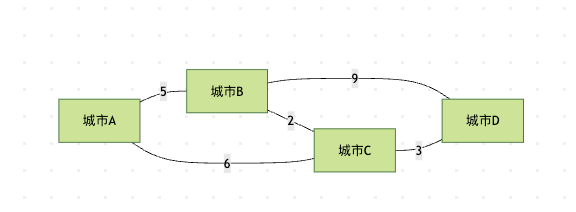
Kruskal算法执行过程
- 边排序:B-C(2), C-D(3), A-B(5), A-C(6), B-D(9)
- 选择B-C(2),加入生成树
- 选择C-D(3),加入生成树
- 选择A-B(5),加入生成树
- 此时所有城市已连接,停止
- 总成本:2 + 3 + 5 = 10
Prim算法执行过程(从A开始)
- 从A出发,可选边A-B(5), A-C(6),选择A-B(5)
- 现在有A和B,可选边B-C(2), B-D(9), A-C(6),选择B-C(2)
- 现在有A,B,C,可选边C-D(3), B-D(9), A-C(6),选择C-D(3)
- 所有城市已连接,停止
- 总成本:5 + 2 + 3 = 10
注意: 虽然两种算法选择了不同顺序的边,但最终的总成本相同,这验证了最小生成树的性质。
6. 总结
通过今天的讨论,我们深入了解了最小生成树问题的两种经典解法:
- Kruskal算法:基于边的贪心算法,适合稀疏图,需要并查集数据结构。
- Prim算法:基于顶点的贪心算法,适合稠密图,需要优先队列。
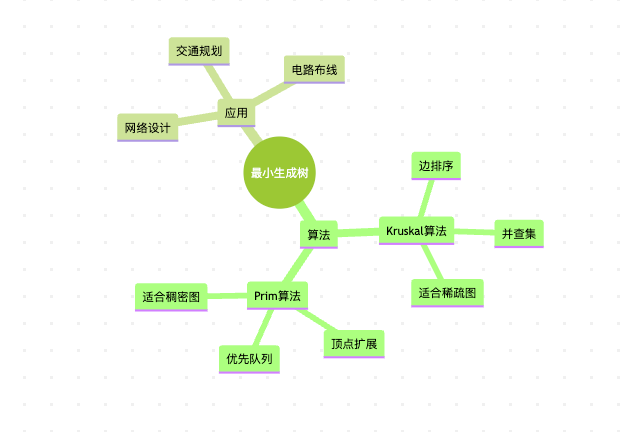
这个思维导图总结了本文的主要内容,帮助大家快速回顾最小生成树的关键概念和算法。
在实际应用中,我建议大家可以:
- 对于大规模稀疏图优先考虑Kruskal算法
- 对于稠密图或需要从特定点开始的情况使用Prim算法
- 根据具体场景和数据结构支持情况选择合适的实现
希望通过本文的分享,能帮助大家更好地理解和应用这两种经典的最小生成树算法。在实际工作中遇到类似问题时,不妨尝试实现这些算法,体验它们的效率和特点。
欢迎随时交流,一起分享关于图算法和优化问题的经验!
